- 2021-04-28 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修3教案:1_1_4程序框图的画法 (2)
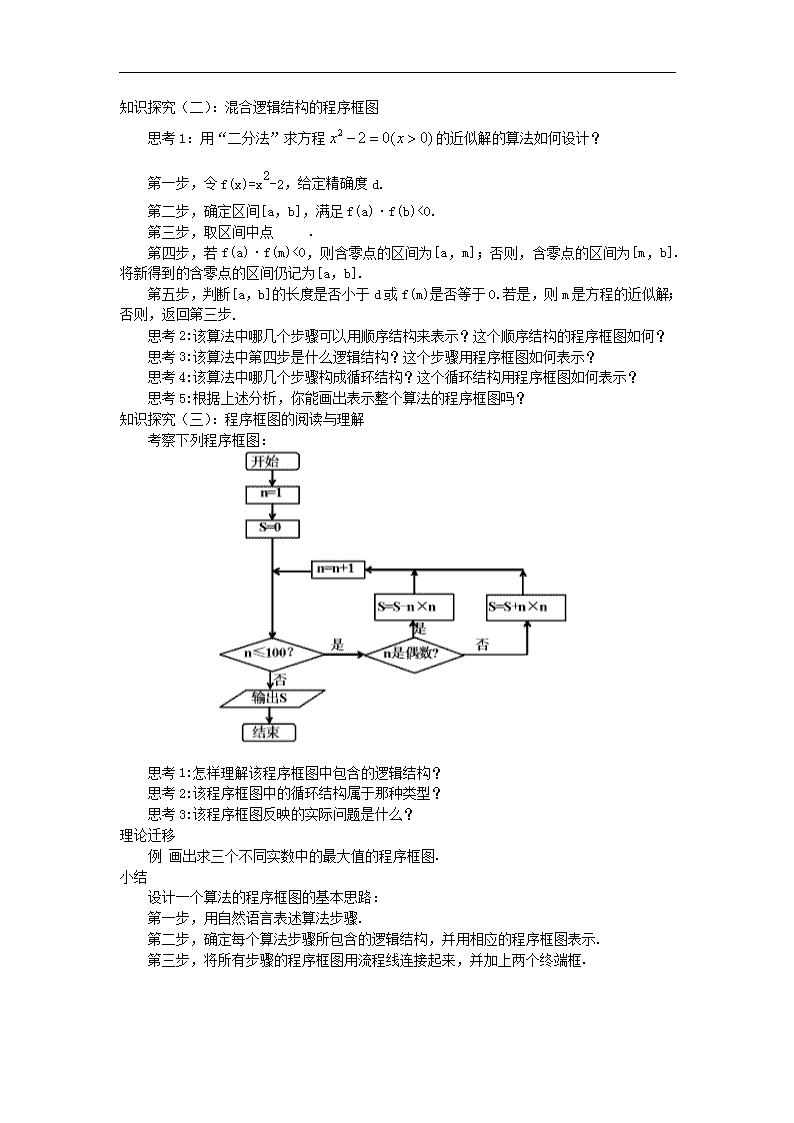
1.1.4 程序框图的画法 【教学目标】: (1) 掌握程序框图的概念;会用通用的图形符号表示算法,掌握算法的三个基本逻辑结构 (2) 掌握画程序框图的基本规则,能正确画出程序框图。 (3) 通过模仿、操作、探索,经历通过设计程序框图表达解决问题的过程;学会灵活、正确地画程序框图。 【教学重点】经过模仿、操作、探索,经历通过设计程序框图表达求解问题的过程,重点是程序框图的基本概念、基本图形符号和3种基本逻辑结构 【教学难点】 难点是能综合运用这些知识正确地画出程序框图。 【学法与教学用具】: 学法: 1、 要弄清各种图形符号的意义,明确每个图形符号的使用环境,图形符号间的联结方式。图形符号都有各自的使用环境和作用 2、 在我们描述算法或画程序框图时,必须遵循一定的逻辑结构,事实证明,无论如何复杂的问题,我们在设计它们的算法时,只需用顺序结构、条件结构和循环结构这三种基本逻辑就可以了,因此我们必须掌握并正确地运用这三种基本逻辑结构。 【教学过程】 知识探究(一):多重条件结构的程序框图 思考1:解关于x的方程ax+b=0的算法步骤如何设计? 第一步,输入实数a,b. 第二步,判断a是否为0.若是,执行第三步;否则,计算 ,并输出x,结束算法. 第三步,判断b是否为0.若是,则输出“方程的解为任意实数”;否则,输出“方程无实数解”. 思考2:该算法的程序框图如何表示? 思考3:你能画出求分段函数的值的程序框图吗? 知识探究(二):混合逻辑结构的程序框图 思考1:用“二分法”求方程的近似解的算法如何设计? 第一步,令f(x)=x2-2,给定精确度d. 第二步,确定区间[a,b],满足f(a)·f(b)<0. 第三步,取区间中点 . 第四步,若f(a)·f(m)<0,则含零点的区间为[a,m];否则,含零点的区间为[m,b].将新得到的含零点的区间仍记为[a,b]. 第五步,判断[a,b]的长度是否小于d或f(m)是否等于0.若是,则m是方程的近似解;否则,返回第三步. 思考2:该算法中哪几个步骤可以用顺序结构来表示?这个顺序结构的程序框图如何? 思考3:该算法中第四步是什么逻辑结构?这个步骤用程序框图如何表示? 思考4:该算法中哪几个步骤构成循环结构?这个循环结构用程序框图如何表示? 思考5:根据上述分析,你能画出表示整个算法的程序框图吗? 知识探究(三):程序框图的阅读与理解 考察下列程序框图: 思考1:怎样理解该程序框图中包含的逻辑结构? 思考2:该程序框图中的循环结构属于那种类型? 思考3:该程序框图反映的实际问题是什么? 理论迁移 例 画出求三个不同实数中的最大值的程序框图. 小结 设计一个算法的程序框图的基本思路: 第一步,用自然语言表述算法步骤. 第二步,确定每个算法步骤所包含的逻辑结构,并用相应的程序框图表示. 第三步,将所有步骤的程序框图用流程线连接起来,并加上两个终端框.查看更多