- 2021-05-06 发布 |
- 37.5 KB |
- 54页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考风向标理科数学集合与函数概念
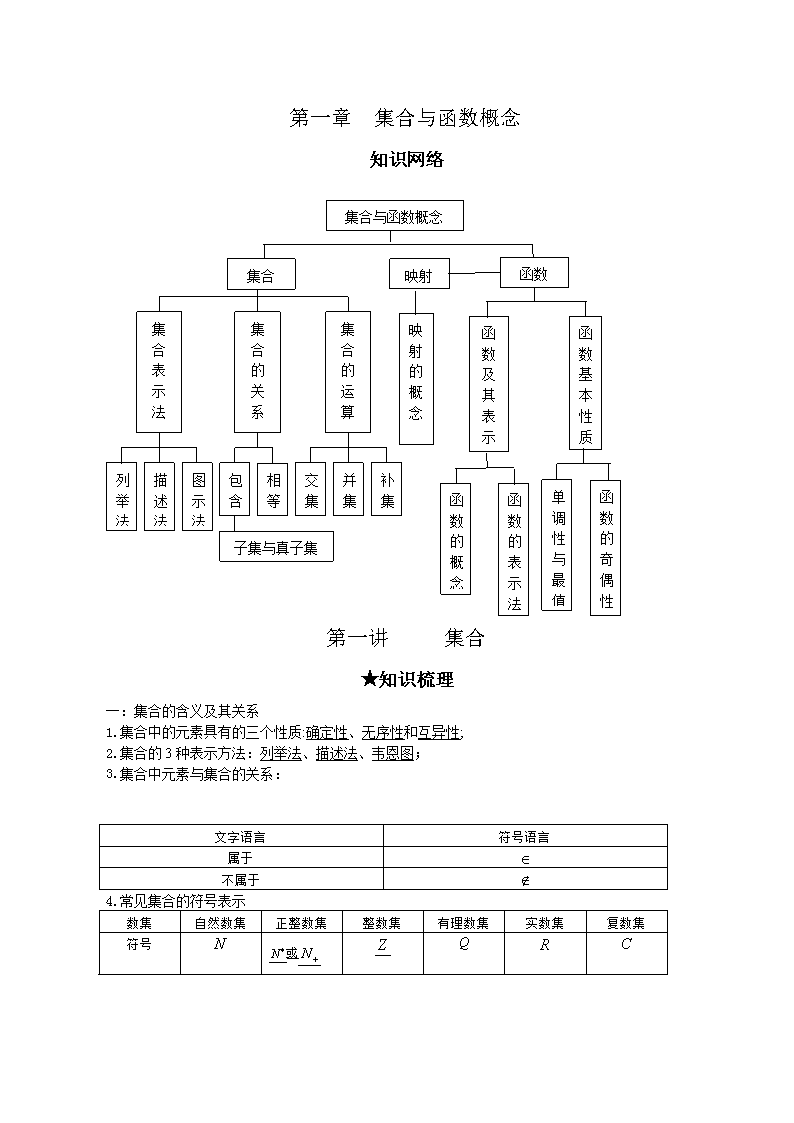
第一章 集合与函数概念 知识网络 第一讲 集合 ★知识梳理 一:集合的含义及其关系 1.集合中的元素具有的三个性质:确定性、无序性和互异性; 2.集合的 3 种表示方法:列举法、描述法、韦恩图; 3.集合中元素与集合的关系: 文字语言 符号语言 属于 不属于 4.常见集合的符号表示 数集 自然数集 正整数集 整数集 有理数集 实数集 复数集 符号 N N 或 N Z Q R C 集合 集 合 表 示 法 集 合 的 运 算 集 合 的 关 系 列 举 法 描 述 法 图 示 法 包 含 相 等 子集与真子集 交 集 并 集 补 集 函数 函 数 及 其 表 示 函 数 基 本 性 质 单 调 性 与 最 值 函 数 的 概 念 函 数 的 奇 偶 性 函 数 的 表 示 法 映射 映 射 的 概 念 集合与函数概念 二: 集合间的基本关系 表示 关系 文字语言 符号语言 相等 集合 A与集合 B 中的所有元素 都相同 BA 且 AB BA 子集 A 中任意一元素均为 B 中的元 素 BA 或 AB 真子集 A 中任意一元素均为 B 中的元 素,且 B 中至少有一元素不是 A 的元素 A B 空集 空集是任何集合的子集,是任 何非空集合的真子集 A , B( B ) 三:集合的基本运算 ①两个集合的交集: A B = x x A x B 且 ; ②两个集合的并集: A B = x x A x B 或 ; ③设全集是 U,集合 A U ,则 UC A x x U x A 且 交 并 补 { | , }A B x x A x B 且 { | , }A B x x A x B 或 UC A x x U x A 且 方法:常用数轴或韦恩图进行集合的交、并、补三种运算. ★重、难点突破 重点:集合元素的特征、集合的三种表示方法、集合的交、并、补三种运算。 难点:正确把握集合元素的特征、进行集合的不同表示方法之间的相互转化,准确进行集合的交、 并、补三种运算。 重难点: 1.集合的概念 掌握集合的概念的关键是把握集合元素的三大特性,要特别注意集合中元素的互异性, 在解题过程中最易被忽视,因此要对结果进行检验; 2.集合的表示法 (1)列举法要注意元素的三个特性;(2)描述法要紧紧抓住代表元素以及它所具有的性质, 如 )(xfyx 、 )(xfyy 、 )(),( xfyyx 等的差别,如果对集合中代表元素认识不清, 将导致求解错误: 问题:已知集合 2 2 1 , 1 , 9 4 3 2 x y x yM x N y 则M N=( ) A. ;B. )2,0(),0,3( ;C. 3,3 ;D. 3,2 [错解]误以为集合M 表示椭圆 1 49 22 yx ,集合 N 表示直线 1 23 yx ,由于这直线过 椭圆的两个顶点,于是错选 B [正解] C; 显然 33 xxM , RN ,故 ]3,3[NM (3)Venn 图是直观展示集合的很好方法,在解决集合间元素的有关问题和集合的运算时常用 Venn 图。 3.集合间的关系的几个重要结论 (1)空集是任何集合的子集,即 A (2)任何集合都是它本身的子集,即 AA (3)子集、真子集都有传递性,即若 BA , CB ,则 CA 4.集合的运算性质 (1)交集:① ABBA ;② AAA ;③ A ;④ ABA , BBA ⑤ BAABA ; (2)并集:① ABBA ;② AAA ;③ AA ;④ ABA , BBA ⑤ ABABA ; (3)交、并、补集的关系 ① ACA U ; UACA U ② )()()( BCACBAC UUU ; )()()( BCACBAC UUU ★热点考点题型探析 考点一:集合的定义及其关系 题型 1:集合元素的基本特征 [例 1](2008 年江西理)定义集合运算: | , ,A B z z xy x A y B .设 1,2 , 0,2A B ,则集合 A B 的所有元素之和为( ) A.0;B.2;C.3;D.6 [解题思路]根据 A B 的定义,让 x在 A中逐一取值,让 y在 B中逐一取值, xy在值就是 A B 的 元素 [解析 ]:正确解答本题 ,必需清楚集合 A B 中的元素,显然,根据题中定义的集合运算知 A B = 4,2,0 ,故应选择 D 【名师指引】这类将新定义的运算引入集合的问题因为背景公平,所以成为高考的一个热点,这时 要充分理解所定义的运算即可,但要特别注意集合元素的互异性。 题型 2:集合间的基本关系 [例 2].数集 ZnnX ,)12( 与 ZkkY ,)14( 之的关系是( ) A. X Y ;B.Y X ; C. YX ;D. YX [解题思路]可有两种思路:一是将 X 和Y 的元素列举出来,然后进行判断;也可依选择支之间的关 系进行判断。 [解析] 从题意看,数集 X 与Y 之间必然有关系,如果 A成立,则 D 就成立,这不可能; 同样,B 也不能成立;而如果 D 成立,则 A、B中必有一个成立,这也不可能,所以只能是 C 【名师指引】新定义问题是高考的一个热点,解决这类问题的办法就是严格根据题中的定义,逐个 进行检验,不方便进行检验的,就设法举反例。 [新题导练] 1.第二十九届夏季奥林匹克运动会将于 2008 年 8 月 8 日在北京举行,若集合 A={参加北京奥运会 比赛的运动员},集合 B={参加北京奥运会比赛的男运动员},集合 C={参加北京奥运会比赛的女运 动员},则下列关系正确的是( ) A. BA B. CB C. CBA D. ACB [解析] D;因为全集为 A,而 CB =全集= A 2 . (2006 • 山 东 改 编 ) 定 义 集 合 运 算 : ByxxyyxB A,,zA 22 , 设 集 合 1,0A , 3,2B ,则集合 BA 的所有元素之和为 [解析]18,根据 BA 的定义,得到 12,6,0A B ,故 BA 的所有元素之和为 18 3. (2007·湖北改编)设 P 和 Q 是两个集合,定义集合 QP QxPxx 且,| ,如果 1log3 xxP , 1 xxQ ,那么 QP 等于 [解析] 31 xx ;因为 )3,0(1log3 xxP , )1,1(1 xxQ ,所以 )3,1(QP 4.研究集合 42 xyxA , 42 xyyB , 4),( 2 xyyxC 之间的关系 [解析] A与C,B与C都无包含关系,而 B A;因为 42 xyxA 表示 42 xy 的定义域,故 RA ; 42 xyyB 表示函数 42 xy 的值域, ),4[ B ; 4),( 2 xyyxC 表示曲线 42 xy 上的点集,可见,B A,而 A与C,B与C都无包 含关系 考点二:集合的基本运算 [例 3] 设集合 0232 xxxA , 0)5()1(2 22 axaxxB (1) 若 2BA ,求实数 a的值; (2)若 ABA ,求实数 a的取值范围若 2BA , [解题思路]对于含参数的集合的运算,首先解出不含参数的集合,然后根据已知条件求参数。 [解析]因为 2,10232 xxxA , (1)由 2BA 知, B2 ,从而得 0)5()1(42 22 aa ,即 0342 aa ,解得 1a 或 3a 当 1a 时, 2,2042 xxB ,满足条件; 当 3a 时, 20442 xxxB ,满足条件 所以 1a 或 3a (2)对于集合 B,由 )3(8)5(4)1(4 22 aaa 因为 ABA ,所以 AB ①当 0 ,即 3a 时, B ,满足条件; ②当 0 ,即 3a 时, 2B ,满足条件; ③当 0 ,即 3a 时, 2,1 AB 才能满足条件, 由根与系数的关系得 7 2 5 521 )1(221 2 2 a a a a ,矛盾 故实数a的取值范围是 3a 【名师指引】对于比较抽象的集合,在探究它们的关系时,要先对它们进行化简。同时,要注意集 合的子集要考虑空与不空,不要忘了集合本身和空集这两种特殊情况. [新题导练] 6.若集合 RxyyS x ,3 , RxxyyT ,12 ,则 TS 是( ) A. S;B. T ;C.;D. 有限集 [解析] A;由题意知,集合 RxyyS x ,3 表示函数 Rxy x ,3 的值域,故 集合 ),0( S ; RxxyyT ,12 表示函数 Rxxy ,12 的值域, ),1[ T ,故 STS 7.已知集合 2),( yxyxM , 4),( yxyxN ,那么集合 NM 为( ) A. 1,3 yx ;B. )1,3( ;C. 1,3 ;D. )1,3( [解析]D; NM 表示直线 2 yx 与直线 4 yx 的交点组成的集合,A、B、C 均不合题意。 8.集合 { | 1 0}A x ax , 2| 3 2 0B x x x ,且 A B B ,求实数a的值. [解析] 10,1, 2 ;先化简 B 得, 1,2B .由于 A B B A B ,故1 A 或 2 A . 因此 1 0a 或2 1 0a ,解得 1a 或 1 2 a . 容易漏掉的一种情况是: A 的情形,此时 0a . 故所求实数a的值为 10,1, 2 . 备选例题 1:已知 1 xyyM , 1),( 22 yxyxN ,则 NM 中的元素个数是( ) A. 0 ;B. 1;C. 2;D.无穷多个 [解析]选 A;集合M 表示函数 1 xy 的值域,是数集,并且 RM ,而集合N 表示满足 122 yx 的有序实数对的集合,即表示圆 122 yx 上的点,是点集。所以,集合M 与集合 N 中 的元素均不相同,因而 NM ,故其中元素的个数为 0 [误区分析]在解答过程中易出现直线 1 xy 与圆 122 yx 有两个交点误选 C;或者误认为 1 xy 中 Ry ,而 122 yx 中 11 y ,从而 ]1,1[NM 有无穷多个解而选 D。注 意,明确集合中元素的属性(是点集还是数集)是准确进行有关集合运算的前提和关键。 备选例题 2:已知集合 A和集合 B各有 12 个元素, BA 含有 4 个元素,试求同时满足下面两个 条件的集合C的个数: (Ⅰ)C BA ,且C中含有 3 个元素; (Ⅱ) AC (表示空集) [解法一]因为 A、 B各有 12 个元素, BA 含有 4 个元素, 因此, BA 的元素个数是 2041212 故满足条件(Ⅰ)的集合C的个数是 3 20C 上面集合中,还满足 AC 的集合C的个数是 3 8C 因此,所求集合C的个数是 10843 8 3 20 CC [解法二]由题目条件可知,属于 B而不属于 A的元素个数是 8412 因此,在 BA 中只含有 A中 1 个元素的所要求的集合C的个数为 2 8 1 12CC 含有 A中 2 个元素的所要求的集合C的个数为 1 8 2 12CC 含有 A中 3 个元素的所要求的集合C的个数为 3 12C 所以,所求集合C的个数是 10843 12 1 8 2 12 2 8 1 12 CCCCC ★抢分频道 基础巩固训练: 1.(09 年吴川市川西中学 09 届第四次月考)设全集 R, ( 3) 0 , 1U A x x x B x x , 则右图中阴 影部分表示的集合为 ( ) A. 0x x ;B. 3 0x x ;C. 3 1x x ;D. 1x x [解析]C;图中阴影部分表示的集合是 BA ,而 03 xxA ,故 13 xxBA 2. (韶关 09 届高三摸底考)已知 2(1 ) 0 , log 0A x x x B x x 则 A B = A. (0,1) ;B. (0, 2);C. )0,( ;D. ( ,0) (0, [解析] A;因为 10 xxA , 10 xxB ,所以 10 xxBA 3. (苏州 09 届高三调研考)集合{ 1,0,1} 的所有子集个数为 [解析]8;集合{ 1,0,1} 的所有子集个数为 823 4.(09 年无锡市高三第一次月考)集合 A中的代表元素设为 x,集合 B中的代表元素设为 y ,若 Bx 且 Ay ,则 A与 B的关系是 [解析] AB 或 A B ;由子集和交集的定义即可得到结论 5.(2008 年天津)设集合 RTSaxaxTxxS ,8|,32| ,则 a的取值范围是 ( ) A. 13 a ;B. 13 a C. 3a 或 1a ;D. 3a 或 1a [解析]A; 5132| xxxxxS 或 , 8| axaxT , RTS 所以 58 1 a a ,从而得 13 a 综合提高训练: 6. 01 mmP , 恒成立对于任意实数xmxmxRmQ 0442 则下列关系中立的是( ) A. P Q ; B.Q P ;C. QP ;D. QP [解析]A;当 0m 时,有 0)4(4)4( 0 2 mm m ,即 01 mRmQ ;当 0m 时, 0442 mxmx 也恒成立,故 01 mRmQ ,所以 P Q 7.设 )(12)( Nnnnf , 5,4,3,2,1P , 7,6,5,4,3Q ,记 PnfNnP )(ˆ , QnfNnQ )(ˆ ,则 )ˆˆ()ˆˆ( PCQQCP NN =( ) U BA A. 3,0 ; B. 2,1 ; C. 5,4,3 ; D. 7,6,2,1 [解析] A;依题意得 2,1,0ˆ P , 3,2,1ˆ Q ,所以 0)ˆˆ( QCP N , 3)ˆˆ( PCQ N ,故应选 A 8.(09 届惠州第一次调研考)设 A、B 是非空集合,定义 { }A B x x A B x A B 且 ,已知 A= 2{ | 2 }x y x x ,B={ | 2 , 0}xy y x , 则 A×B 等于( ) A. 0, ;B. 0,1 2, ;C. 0,1 2, ;D. 0,1 (2, ) [解析]D; 22 0 0 2x x x ,∴A=[0,2], 0 2 1xx ,∴B=(1,+∞), ∴A∪B=[0, +∞),A∩B=(1,2],则 A×B= 0,1 (2, ) 第 2 讲 函数与映射的概念 ★知识梳理 1.函数的概念 (1)函数的定义: 设 BA、 是两个非空的数集,如果按照某种对应法则 f ,对于集合 A中的每一个数 x,在集合 B 中都有唯一确定的数和它对应,那么这样的对应叫做从 A 到 B 的一个函数,通常记为 Axxfy ),( (2)函数的定义域、值域 在函数 Axxfy ),( 中, x叫做自变量, x的取值范围 A叫做 )(xfy 的定义域;与 x的 值相对应的 y 值叫做函数值,函数值的集合 Axxf )( 称为函数 )(xfy 的值域。 (2)函数的三要素:定义域、值域和对应法则 2.映射的概念 设 BA、 是两个集合,如果按照某种对应法则 f ,对于集合 A中的任意元素,在集合 B中都 有唯一确定的元素与之对应,那么这样的单值对应叫做从 A到 B的映射,通常记为 BAf : ★重、难点突破 重点:掌握映射的概念、函数的概念,会求函数的定义域、值域 难点:求函数的值域和求抽象函数的定义域 重难点:1.关于抽象函数的定义域 求抽象函数的定义域,如果没有弄清所给函数之间的关系,求解容易出错误 问题 1:已知函数 )(xfy 的定义域为 ][ ba, ,求 )2( xfy 的定义域 [误解]因为函数 )(xfy 的定义域为 ][ ba, ,所以 bxa ,从而 222 bxa 故 )2( xfy 的定义域是 ]2,2[ ba [正解]因为 )(xfy 的定义域为 ][ ba, ,所以在函数 )2( xfy 中, bxa 2 , 从而 22 bxa ,故 )2( xfy 的定义域是 ]2,2[ ba 即本题的实质是求 bxa 2 中 x的范围 问题 2:已知 )2( xfy 的定义域是 ][ ba, ,求函数 )(xfy 的定义域 [误解]因为函数 )2( xfy 的定义域是 ][ ba, ,所以得到 bxa 2 ,从而 22 bxa ,所以函数 )(xfy 的定义域是 ]2,2[ ba [正解]因为函数 )2( xfy 的定义域是 ][ ba, ,则 bxa ,从而 222 bxa 所以函数 )(xfy 的定义域是 ]2,2[ ba 即本题的实质是由 bxa 求 2x 的范围 即 )(xf 与 )2( xf 中 x含义不同 2.求值域的几种常用方法 (1)配方法:对于(可化为)“二次函数型”的函数常用配方法,如求函数 4cos2sin 2 xxy , 可变为 2)1(cos4cos2sin 22 xxxy 解决 (2)基本函数法:一些由基本函数复合而成的函数可以利用基本函数的值域来求,如函数 )32(log 2 2 1 xxy 就是利用函数 uy 2 1log 和 322 xxu 的值域来求。 (3)判别式法:通过对二次方程的实根的判别求值域。如求函数 22 12 2 xx xy 的值域 由 22 12 2 xx xy 得 012)1(22 yxyyx ,若 0y ,则得 2 1 x ,所以 0y 是函数 值 域 中 的 一 个 值 ; 若 0y , 则 由 0)12(4)]1(2[ 2 yyy 得 0 2 133 2 133 yy 且 ,故所求值域是 ] 2 133, 2 133[ (4)分离常数法:常用来求“分式型”函数的值域。如求函数 1cos 3cos2 x xy 的值域,因为 1cos 52 1cos 3cos2 xx xy ,而 ]2,0(1cos x ,所以 ] 2 5,( 1cos 5 x ,故 ] 2 1,( y (5)利用基本不等式求值域:如求函数 4 3 2 x xy 的值域 当 0x 时, 0y ;当 0x 时, x x y 4 3 ,若 0x ,则 4424 x x x x 若 0x ,则 4)4()(2)4(4 x x x x x x ,从而得所求值域是 ] 4 3, 4 3[ (6)利用函数的单调性求求值域:如求函数 ])2,1[(22 24 xxxy 的值域 因 )14(228 23 xxxxy ,故函数 ])2,1[(22 24 xxxy 在 ) 2 1,1( 上递减、在 )0, 2 1( 上递增、在 ) 2 1,0( 上递减、在 )2, 2 1( 上递增,从而可得所求值域为 ]30, 8 15[ (7)图象法:如果函数的图象比较容易作出,则可根据图象直观地得出函数的值域(求某些分段 函数的值域常用此法)。 ★热点考点题型探析 考点一:判断两函数是否为同一个函数 [例 1] 试判断以下各组函数是否表示同一函数? (1) 2)( xxf , 3 3)( xxg ; (2) x x xf )( , ;01 ,01 )( x x xg (3) 12 12)( n nxxf , 1212 )()( nn xxg (n∈N*); (4) xxf )( 1x , xxxg 2)( ; (5) 12)( 2 xxxf , 12)( 2 tttg [解题思路]要判断两个函数是否表示同一个函数,就要考查函数的三要素。 [解析] (1)由于 xxxf 2)( , xxxg 3 3)( ,故它们的值域及对应法则都不相同,所以 它们不是同一函数. (2)由于函数 x x xf )( 的定义域为 ),0()0,( ,而 ;01 ,01 )( x x xg 的定义域为 R, 所以它们不是同一函数. (3)由于当 n∈N*时,2n±1 为奇数,∴ xxxf n n 12 12)( , xxxg nn 1212 )()( ,它们 的定义域、值域及对应法则都相同,所以它们是同一函数. (4)由于函数 xxf )( 1x 的定义域为 0xx ,而 xxxg 2)( 的定义域为 10 xxx 或 ,它们的定义域不同,所以它们不是同一函数. (5)函数的定义域、值域和对应法则都相同,所以它们是同一函数. [答案](1)、(2)、(4)不是;(3)、(5)是同一函数 【名师指引】构成函数的三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系确 定的,所以,如果两个函数的定义域和对应关系完全一致,即称这两个函数为同一函数。第(5)小 题易错判断成它们是不同的函数。原因是对函数的概念理解不透,在函数的定义域及对应法则 f不变的 条件下,自变量变换字母对于函数本身并无影响,比如 1)( 2 xxf , 1)( 2 ttf , 1)1()1( 2 uuf 都可视为同一函数. [新题导练] 1.(2009·佛山) 下列函数中与函数 xy 相同的是( ) A .y = ( x )2 ; B. y = 3 3t ; C. y = 2x ; D. y= x x 2 [解析] B;因为 y = 3 3t t ,所以应选择 B 2.(09 年重庆南开中学)与函数 )12lg(1.0 xy 的图象相同的函数是 ( ) A. ) 2 1(12 xxy ;B. 12 1 x y ;C. ) 2 1( 12 1 x x y ; D. | 12 1| x y [解析] C;根据对数恒等式得 12 1101.0 12 1lg)12lg( x y xx ,且函数 )12lg(1.0 xy 的定义域为 ), 2 1( ,故应选择 C 考点二:求函数的定义域、值域 题型 1:求有解析式的函数的定义域 [例 2].(08 年湖北)函数 )(xf )4323ln(1 22 xxxx x 的定义域为( ) A. ),2[)4,( ;B. )1,0()0,4( ;C. ]1,0()0,4[, ;D. )1,0()0,4[, [解题思路]函数的定义域应是使得函数表达式的各个部分都有意义的自变量的取值范围。 [解析]欲使函数 )(xf 有意义,必须并且只需 0 04323 043 023 22 2 2 x xxxx xx xx )1,0()0,4[ x ,故应选择D 【名师指引】如没有标明定义域,则认为定义域为使得函数解析式有意义的 x的取值范围,实际操 作时要注意:①分母不能为 0;② 对数的真数必须为正;③偶次根式中被开方数应为非负数;④零 指数幂中,底数不等于 0;⑤负分数指数幂中,底数应大于 0;⑥若解析式由几个部分组成,则定 义域为各个部分相应集合的交集;⑦如果涉及实际问题,还应使得实际问题有意义,而且注意:研 究函数的有关问题一定要注意定义域优先原则,实际问题的定义域不要漏写。 题型 2:求抽象函数的定义域 [例 3](2006·湖北)设 x xxf 2 2lg ,则 x fxf 2 2 的定义域为( ) A. 4,00,4 ;B. 4,11,4 ;C. 2,11,2 ;D. 4,22,4 [解题思路]要求复合函数 x fxf 2 2 的定义域,应先求 )( xf 的定义域。 [解析]由 2 0 2 x x 得, ( )f x 的定义域为 2 2x ,故 2 2, 2 22 2. x x 解得 4, 1 1,4x 。故 x fxf 2 2 的定义域为 4,11,4 .选 B. 【名师指引】求复合函数定义域,即已知函数 ( )f x 的定义为[ , ]a b ,则函数 [ ( )]f g x 的定义域是满 足不等式 ( )a g x b 的 x 的取值范围;一般地,若函数 [ ( )]f g x 的定义域是 [ , ]a b ,指的是 [ , ]x a b ,要求 ( )f x 的定义域就是 [ , ]x a b 时 ( )g x 的值域。 题型 3;求函数的值域 [例 4]已知函数 )(6242 Raaaxxy ,若 0y 恒成立,求 32)( aaaf 的值域 [解题思路]应先由已知条件确定a取值范围,然后再将 )(af 中的绝对值化去之后求值域 [解析]依题意, 0y 恒成立,则 0)62(416 2 aa ,解得 2 31 a , 所以 4 17) 2 3()3(2)( 2 aaaaf ,从而 4)1()( max faf , 4 19) 2 3()( min faf , 所以 )(af 的值域是 ]4, 4 19[ 【名师指引】求函数的值域也是高考热点,往往都要依据函数的单调性求函数的最值。 [新题导练] 3.(2008 安徽文、理)函数 2 2 1 ( ) log ( 1) x f x x 的定义域为 . [解析] [3, ) ;由 11,01 012 xx x 解得 3x 4.定义在 R上的函数 ( )y f x 的值域为[ , ]a b ,则函数 ( 1)y f x 的值域为( ) A.[ 1, 1]a b ;B.[ , ]a b ;C.[ 1, 1]a b ;D.无法确定 [解析] B;函数 ( 1)y f x 的图象可以视为函数 ( )y f x 的图象向右平移一个单位而得到,所以, 它们的值域是一样的 5.(2008 江西改) 若函数 ( )y f x 的定义域是 ]3,1[ ,则函数 (2 )( ) 1 f xg x x 的定义域是 [解析 ] ] 2 3,1()1, 2 1[ ;因为 ( )f x 的定义域为 ]3,1[ ,所以对 ( )g x , 321 x 但 1x 故 ] 2 3,1()1, 2 1[ x 6.(2008 江西理改)若函数 ( )y f x 的值域是 ]3, 3 2[ ,则函数 1 ( ) F x f x f x 的值域 是 [解析] ] 3 10,2[ ; )(xF 可以视为以 )(xf 为变量的函数,令 )(xft ,则 )3 3 2(1 t t tF 22 2 2 )1)(1(111 t tt t t t F ,所以, t tF 1 在 ]1, 3 2[ 上是减函数,在 ]3,1[ 上是增函数, 故 )(xF 的最大值是 3 10 ,最小值是 2 考点三:映射的概念 [例 5] (06 陕西)为确保信息安全,信息需加密传输,发送方由明文密文(加密),接收方由 密文明文(解密),已知加密规则为:明文 , , ,a b c d 对应密文 2 , 2 , 2 3 , 4 .a b b c c d d 例如, 明文1, 2,3, 4 对应密文5,7,18,16.当接收方收到密文14,9, 23, 28时,则解密得到的明文为( ) A.7,6,1, 4;B.6, 4,1,7;C. 4,6,1,7;D.1,6, 4,7 [解题思路] 密文与明文之间是有对应规则的,只要按照对应规则进行对应即可。 [解析] 当接收方收到密文 14,9,23,28 时, 有 2 14 2 9 2 3 23 4 28 a b b c c d d ,解得 6 4 1 7 a b c d ,解密得到的明文为 C. 【名师指引】理解映射的概念,应注意以下几点: (1)集合 A、B及对应法则 f是确定的,是一个整体系统; (2)对应法则有“方向性”,即强调从集合 A到集合 B的对应,它与从集合 B到集合 A的对应 关系一般是不同的; (3)集合 A中每一个元素,在集合 B中都有象,并且象是唯一..的,这是映射区别于一般对应 的本质特征; (4)集合 A中不同元素,在集合 B中对应的象可以是同一个; (5)不要求集合 B中的每一个元素在集合 A中都有原象. [新题导练] 7.集合 A={3,4},B={5,6,7},那么可建立从 A到 B的映射个数是__________,从 B到 A的映 射个数是__________. [解析] 9 , 8;从 A到 B可分两步进行:第一步 A中的元素 3 可有 3 种对应方法(可对应 5 或 6 或 7),第二步 A中的元素 4 也有这 3 种对应方法.由乘法原理,不同的映射种数 N1=3×3=9.反之 从 B到 A,道理相同,有 N2=2×2×2=8 种不同映射. 8.若 f :y=3x+1 是从集合 A={1,2,3,k}到集合 B={4,7,a4,a2+3a}的一个映射,求自然数 a、k 的值及集合 A、B. [解析] a=2,k=5,A={1,2,3,5},B={4,7,10,16}; ∵f(1)=3×1+1=4,f(2)=3×2+1=7,f(3)=3×3+1=10,f(k)=3k+1,由映射的定义知(1) ,133 ,10 2 4 kaa a 或(2) .13 ,103 4 2 ka aa ∵a∈N,∴方程组(1)无解. 解方程组(2),得 a=2 或 a=-5(舍),3k+1=16,3k=15,k=5. ∴A={1,2,3,5},B={4,7,10,16}. 备选例题:(03 年上海)已知集合M 是满足下列性质的函数 )(xf 的全体:存在非零常数T ,对 任意 Rx ,有 )()( xTfTxf 成立。 (1)函数 xxf )( 是否属于集合M ?说明理由; (2)设函数 )1,0()( aaaxf x 的图象与 xy 的图象有公共点,证明: Maxf x )( [解析](1)对于非零常数 T,f(x+T)=x+T, Tf(x)=Tx. 因为对任意 x∈R,x+T= Tx不能恒成立,所以 f(x)= .Mx (2)因为函数 f(x)=ax(a>0 且 a≠1)的图象与函数 y=x的图象有公共点, 所以方程组: xy ay x 有解,消去 y 得 ax=x, 显然 x=0 不是方程 ax=x的解,所以存在非零常数 T,使 aT=T. 于是对于 f(x)=ax有 )()( xTfaTaaaTxf xxTTx 故 f(x)=ax∈M. ★抢分频道 基础巩固训练: 1.(2007·广东改编) 已知函数 x xf 1 1)( 的定义域为 N , )1ln()( xxg 的定义域为M ,则 NM [解析] ),( ;因为 ( 1, ), ( ,1)M N ,故 RNM 2.函数 )23(log 3 1 xy 的定义域是 [解析] 2 3( ,1];由 1230 x 得到 1 3 2 x 3.函数 12 12 x x y 的值域是 [解析] )1,1( ;由 12 12 x x y 知 1y ,从而得 y yx 1 12 ,而 02 x ,所以 0 1 1 y y ,即 11 y 4.(广东从化中学 09 届月考)从集合 A 到 B 的映射中,下列说法正确的是( ) A.B 中某一元素b的原象可能不只一个;B.A 中某一元素 a的象可能不只一个 C.A 中两个不同元素的象必不相同; D.B 中两个不同元素的原象可能相同 [解析]A;根据映射的定义知可排除 B、C、D 5.(深圳中学 09 届高三第一学段考试)下列对应法则 f 中,构成从集合 A 到集合 B的映射是( ) A. 2||:,},0|{ xyxfRBxxA B. 2:},4{},2,0,2{ xyxfBA C. 2 1:},0|{, x yxfyyBRA D. 2 :},1,0{},2,0{ xyxfBA [解析]D;根据映射的定义知,构成从集合 A 到集合 B的映射是 D 6.(09 年执信中学)若函数 2 3 4y x x 的定义域为[0, ]m ,值域为 25[ 4] 4 , ,则m的取值范围是 ( ) A. 4,0 ;B. 3[ 3] 2 ,; C. 3[ ] 2 ,4 ;D. 3[ 2 , ) [解析]B;因为函数 2 3 4y x x 即为 4 25) 2 3( 2 xy ,其图象的对称轴为直线 2 3 x , 其最小值为 4 25 ,并且当 0x 及 3x 时, 4y ,若定义域为[0, ]m ,值域为 25[ 4] 4 , ,则 3 2 3 m 综合提高训练: 8.(05 天津改)设函数 x xxf 2 2ln)( ,则函数 )1() 2 ()( x fxfxg 的定义域是 [解析] )4, 2 1() 2 1,4( ;由 0 2 2 x x 得, ( )f x 的定义域为 22 x 。故 212 2 2 2 x x 解得 2 14 x 或 4 2 1 x 。 9.设函数 2 1)( 2 xxxf 的定义域是 ]1,[ nn ( n是正整数),那么 )(xf 的值域中共有 个整数 [解析] 22 n ;因为 4 1) 2 1( 2 1)( 22 xxxxf ,可见, )(xf 在 ]1,[ nn (n是正整数)上 是增函数,又 22) 2 1(] 2 1)1()1[()()1( 22 nnnnnnfnf 所以,在 )(xf 的值域中共有 22 n 个整数 第 3 讲 函数的表示方法 ★知识梳理 一、函数的三种表示法:图象法、列表法、解析法 1.图象法:就是用函数图象表示两个变量之间的关系; 2.列表法:就是列出表格来表示两个变量的函数关系; 3.解析法:就是把两个变量的函数关系,用等式来表示。 二、分段函数 在自变量的不同变化范围中,对应法则用不同式子来表示的函数称为分段函数。 ★重、难点突破 重点:掌握函数的三种表示法-----图象法、列表法、解析法,分段函数的概念 难点:分段函数的概念,求函数的解析式 重难点:掌握求函数的解析式的一般常用方法: (1)若已知函数的类型(如一次函数、二次函数),则用待定系数法; (2)若已知复合函数 )]([ xgf 的解析式,则可用换元法或配凑法; 问题 1.已知二次函数 )(xf 满足 564)12( 2 xxxf ,求 )(xf 方法一:换元法 令 )(12 Rttx ,则 2 1 tx ,从而 )(955 2 16) 2 1(4)( 22 Rttttttf 所以 )(95)( 2 Rxxxxf 方法二:配凑法 因为 9)12(5)12(410)12(564)12( 222 xxxxxxxf 所以 )(95)( 2 Rxxxxf 方法三:待定系数法 因为 )(xf 是二次函数,故可设 cbxaxxf 2)( ,从而由 564)12( 2 xxxf 可求出 951 cba 、、 ,所以 )(95)( 2 Rxxxxf (3)若已知抽象函数的表达式,则常用解方程组消参的方法求出 )(xf 问题 2:已知函数 )(xf 满足 x x fxf 3)1(2)( ,求 )(xf 因为 x x fxf 3)1(2)( ① 以 x 1 代 x得 x xf x f 13)(2)1( ② 由①②联立消去 )1( x f 得 )0(2)( xx x xf ★热点考点题型探析 考点 1:用图像法表示函数 [例 1] (09 年广东南海中学)一水池有 2个进水口, 1个出水口,一个口的进、出水的速度如图甲、 乙所示.某天0点到6点,该水池的蓄水量如图丙所示.给出以下3个论断: 进水量 出水量 蓄水量 甲 乙 丙 (1)0 点到3点只进水不出水;(2)3点到 4 点不进水只出水;(3)4 点到6点不进水不出水. 则一定不正确...的论断是 (把你认为是符合题意的论断序号都填上) . [解题思路]根据题意和所给出的图象,对三个论断进行确认即可。 [解析]由图甲知,每个进水口进水速度为每小时 1 个单位,两个进水口 1个小时共进水 2 个单位,3 个小时共进水 6 个单位,由图丙知①正确;而由图丙知,3 点到 4 点应该是有一个进水口进水,出 水口出水,故②错误;由图丙知,4 点到 6 点可能是不进水不出水,也可能是两个进水口都进水, 同时出水口也出水,故③不一定正确。从而一定不正确...的论断是(2) 【名师指引】象这类给出函数图象让考生从图象获取信息的问题是目前高考的一个热点,它要求考 生熟悉基本的函数图象特征,善于从图象中发现其性质。高考中的热点题型是“知式选图”和“知 图选式”。 [新题导练] 时间0 1 1 时间0 2 1 时间0 3 4 6 6 5 1. (05 辽宁改 )一给定函数 )(xfy 的图象在下列图中,并且对任意 )1,0(1 a ,由关系式 0)(1 nn afa 得到的数列 }{ na 满足 )(0 * 1 Nnaa nn ,则该函数的图象是( ) A B C D [ 解 析 ] A. ; 令 1 n n a x a y ,则 ( )y f x 等价于 )(1 nn afa , ( )y f x 是由点 1( , )n na a 组 成,而又知道 1n na a ,所以每各点都在 y=x的上方。 2.(2005·湖北)函数 |1|||ln xey x 的图象大致是( ) [解析] D;当 1x 时, 1)1( xxy ,可以排除 A 和 C;又当 2 1 x 时, 2 3 y ,可以排除 B 考点 2:用列表法表示函数 [例 2] (07 年北京)已知函数 ( )f x , ( )g x 分别由下表给出 则 [ (1)]f g 的值为 ;满足 [ ( )] [ ( )]f g x g f x 的 x的值是 [解题思路]这是用列表的方法给出函数,就依照表中的对应关系解决问题。 [解析]由表中对应值知 [ (1)]f g = (3) 1f ; 当 1x 时, [ (1)] 1, [ (1)] (1) 3f g g f g ,不满足条件 x 1 2 3 ( )f x 1 3 1 x 1 2 3 ( )g x 3 2 1 当 2x 时, [ (2)] (2) 3, [ (2)] (3) 1f g f g f g ,满足条件, 当 3x 时, [ (3)] (1) 1, [ (3)] (1) 3f g f g f g ,不满足条件, ∴满足 [ ( )] [ ( )]f g x g f x 的 x的值是 2x 【名师指引】用列表法表示函数具有明显的对应关系,解决问题的关键是从表格发现对应关系,用 好对应关系即可。 [新题导练] 3.(09 年山东梁山)设 f、g都是由 A到 A的映射,其对应法则如下表(从上到下): 映射 f的对应法则是表 1 原象 1 2 3 4 象 3 4 2 1 映射 g的对应法则是表 2 则与 )]1([gf 相同的是( ) A. )]1([ fg ;B. )]2([ fg ;C. )]3([ fg ;D. )]4([ fg [解析] A;根据表中的对应关系得, 1)4()]1([ fgf , 1)3()]1([ gfg 4.(04 年江苏改编)二次函数 cbxaxy 2 ( x∈R)的部分对应值如下表: x -3 -2 -1 0 1 2 3 4 y 6 0 -4 -6 -6 -4 0 6 则不等式 02 cbxax 的解集是 [解析] )3,2( ;由表中的二次函数对应值可得,二次方程 02 cbxax 的两根为-2和 3,又根 据 )2()0( ff 且 )3()0( ff 可知 0a ,所以不等式 02 cbxax 的解集是 )3,2( 考点 3:用解析法表示函数 题型 1:由复合函数的解析式求原来函数的解析式 [例 3] (04 湖北改编)已知 ) 1 1( x xf = 2 2 1 1 x x ,则 )(xf 的解析式可取为 [解题思路]这是复合函数的解析式求原来函数的解析式,应该首选换元法 原象 1 2 3 4 象 4 3 1 2 [解析] 令 t x x 1 1 ,则 1 1 t tx ,∴ 1 2)( 2 t ttf .∴ 1 2)( 2 x xxf . 故应填 21 2 x x 【名师指引】求函数解析式的常用方法有:① 换元法( 注意新元的取值范围);② 待定系数 法(已知函数类型如:一次、二次函数、反比例函数等);③整体代换(配凑法);④构造方程组 (如自变量互为倒数、已知 )(xf 为奇函数且 )(xg 为偶函数等)。 题型 2:求二次函数的解析式 [例 4] (普宁市城东中学 09 届高三第二次月考)二次函数 )(xf 满足 xxfxf 2)()1( ,且 1)0( f 。 ⑴求 )(xf 的解析式; ⑵在区间 ]1,1[ 上, )(xfy 的图象恒在 mxy 2 的图象上方,试确定实数m的范围。 [解题思路](1)由于已知 )(xf 是二次函数,故可应用待定系数法求解;(2)用数表示形,可得 求 )(2 xfmx 对于 ]1,1[x 恒成立,从而通过分离参数,求函数的最值即可。 [解析]⑴设 2( ) ( 0)f x ax bx c a ,则 2 2( 1) ( ) [ ( 1) ( 1) ] ( ) 2 f x f x a x b x c ax bx c ax a b 与已知条件比较得: 2 2, 0 a a b 解之得, 1, 1 a b 又 (0) 1f c , 2( ) 1f x x x ⑵由题意得: 2 1 2x x x m 即 2 3 1m x x 对 1,1x 恒成立, 易得 2 min( 3 1) 1m x x 【名师指引】如果已知函数的类型,则可利用待定系数法求解;通过分离参数求函数的最值来获得 参数的取值范围是一种常用方法。 [新题导练] 5.(06 全国卷二改编)若 xxf 2cos3)(sin ,则 )] 2 [sin( xf [解析] x2cos3 ; )] 2 [sin( xf 2 2(sin ) 3 cos 2 3 (1 2sin ) 2sin 2f x x x x 所以 2( ) 2 2f x x ,因此 2 2(cos ) 2cos 2 (2cos 1) 3 3 cos 2f x x x x 6.(09 年潮州金山中学)设 ( )y f x 是一次函数,若 0 1f 且 1 , 4 , 13f f f 成 等比数列,则 2 4 2f f f n ; [解析] )32( nn ;设 bkxxf )( ,由 1)0( f 得 1b ,从而 1)( kxxf 又由 1 , 4 , 13f f f 成等比数列得 2)14()113)(1( kkk ,解得 2k 所以 12)( xxf , 2 4 2f f f n )32(]12[]142[]122[ nnn 7.(华侨中学 09 届第 3 次月考(09 年中山))设 1 1 xf x x ,又记 1 1, , 1,2, ,k kf x f x f x f f x k 则 2008f x ( ) A. 1 1 x x ;B. 1 1 x x ;C. x;D. 1 x ; [解析] C;由已知条件得到 x x x x x xf xf xffxf 1 1 11 1 11 )(1 )(1 )]([)( 1 1 12 , 1 1 11 11 )(1 )(1 )]([)( 1 1 23 x x x x xf xf xffxf , x x x x x xf xf xffxf 1 11 1 11 )(1 )(1 )]([)( 3 3 34 , x xxffxf 1 1)]([)( 45 可见, )(xf n 是以 4 为周期的函数,而 45022008 ,所以, xxfxf )()( 42008 8.设二次函数 )(xf 满足 )2()2( xfxf ,且其图象在 y轴上的截距为 1,在 x轴上截得的线 段长为 2 ,求 )(xf 的解析式。 [解析] 1 7 8 7 2)( 2 xxxf ;设 f(x)=ax2+bx+c, 由 f(x)满足 f(x-2)=f(-x-2),可得函数 y=f(x)的对称轴为 x=-2,所以 2 2 b a 由 y=f(x)图象在 y轴上的截距为 1,可得 (0) 1f ,即 c=1 由 y=f(x) 图象在 x轴上截得的线段长为 2 ,可得 2 2 1 2 1 2 1 2| | ( ) 4 ( ) 4 2b cx x x x x x a a 所以联立方程组 2( ) 4 2 1 2 2 b c a a c b a ,可解得 2 7 8 7 1 a b c 所以 f(x)= 1 7 8 7 2 2 xx . 考点 4:分段函数 题型 1:根据分段函数的图象写解析式 [例 5] (07 年湖北)为了预防流感,某学校对教室用药 物消毒法进行消毒。已知药物释放过程中,室内每立 方 米 空 气中含药量 y(毫克)与时间 t(小时)成正比;药物 释 放 完 毕后,y与 t的函数关系式为 a y 1 16 1 (a为常数), 如 图 所 示,根据图中提供的信息,回答下列问题: (Ⅰ)从药物释放开妈,每立方米空气中的含药量 y (毫克) 与时间 t(小时)之间的函数关系式为 ; (Ⅱ)据测定,当空气中每立方米的含药量降低到 0.25 毫克以下时,学生方可进教室,那么从药物 释放开始,至少需要经过 小时后,学生才能回到教室。 [思路点拨]根据题意,药物释放过程的含药量 y(毫克)与时间 t是一次函数,药物释放完毕后,y 与 t的函数关系是已知的,由特殊点的坐标确定其中的参数,然后再由所得的表达式解决(Ⅱ) [解析] (Ⅰ)观察图象,当 1.00 t 时是直线,故 ty 10 ;当 1.0t 时,图象过 )1,1.0( 所以 a 1.0 16 11 ,即 1.0a ,所以 1.0,) 16 1( 1.00,10 1.0 t tt y t (Ⅰ) 6.0 16 1 16 125.0 16 1 5.01.01.0 t aa ,所以至少需要经过 6.0 小时 【名师指引】分段函数的每一段一般都是由基本初等函数组成的,解决办法是分段处理。 题型 2:由分段函数的解析式画出它的图象 例 6] (2006·上海)设函数 54)( 2 xxxf ,在区间 ]6,2[ 上画出函数 )(xf 的图像。 [思路点拨]需将来绝对值符号打开,即先解 0542 xx ,然后依分界点将函数分段表示,再画 出图象。 [解析] 2 2 2 4 5 2 1 5 6 ( ) 4 5 ( 4 5) 1 5 x x x x f x x x x x x 或 ,如右上图. 【名师指引】分段函数的解决办法是分段处理,要注意分段函数的表示方法,它是用联立符号将函 数在定义域的各个部分的表达式依次表示出来,同时附上自变量的各取值范围。 [新题导练] 9.(09 年潮州金山中学)已知函数 2 2 3 ( 0) ( ) 1 ( 0) x x f x x x ,则 1f f [解析] 2;由已知得到 21)1()1()312()]1([ 2 ffff 10.(06 山东改编)设 ,2),1(log .2,2 )( 2 2 1 xx x xf x 则不等式 02)( xf 的解集为 [解析] ),5()2,1( ;当 2x 时,由 02)( xf 得 22 1 x ,得 21 x 当 2x 时,由 02)( xf 得 2)1(log 2 2 x ,得 5x 备选例题 1: (2005·江西)已知函数 bax xxf 2 )( (a,b 为常数)且方程 f(x)-x+12=0 有两个实根 为 x1=3, x2=4. (1)求函数 f(x)的解析式;(2)设 k>1,解关于 x的不等式; x kxkxf 2 )1()( [解析](1)将 0124,3 2 21 x bax xxx 分别代入方程 得 2 9 9 13 , ( ) ( 2). 16 2 28 4 a xa b f x x b x a b 解得 所以 (2)不等式即为 0 2 )1(, 2 )1( 2 22 x kxkx x kxk x x 可化为 即 .0))(1)(2( kxxx ①当 ).,2(),1(,21 kxk 解集为 ②当 );,2()2,1(0)1()2(,2 2 xxxk 解集为不等式为时 ③ ),()2,1(,2 kxk 解集为时当 . 备选例题 2:(06 重庆)已知定义域为 R 的函数 ( )f x 满足 2 2( ) ( ) .f f x x x f x x x (I)若 (2) 3f ,求 (1)f ;又若 (0)f a ,求 ( )f a ; (II)设有且仅有一个实数 0x ,使得 0 0( )f x x ,求函数 ( )f x 的解析表达式 2 2 2 2 2 ) ( ) 2) (2) 2 2 2 3 2 2, (1) 1 f(0)=a, f( 0 0) 0 0, ( ) x f x x x f f a a f a a 2 2 2 解:(I)因为对任意x R,有f(f(x)-x 所以f(f(2)-2 又由f(2)=3,得f(3-2 ) 即 若 则 即 2 2 0 0 0 2 0 2 0 0 0 0 0 2 0 0 0 0 0 0 2 2 0 (II) ( ( ) ) ( ) . ( ) , ( ) ( ) ( ) 0 ( ) 0 ( ) x R f f x x x f x x x x f x x x R f x x x x x x f x x x x f x x x x x x x f x x x f x x 因为对任意 ,有 又因为有且只有一个实数 ,使得 所以对任意 有 在上式中令 ,有 又因为 ,所以 ,故 =0或 =1 若 =0,则 ,即 2 0 2 2 0 2 0 ( ) 1, ( ) 1. ( ) 1 ( ) x x x x x x f x x x f x x x f x x x x R 但方程 有两个不相同实根,与题设条件矛盾。故 若 =1,则有 即 易验证该函数满足题设条件。 综上,所求函数为 ★抢分频道 基础巩固训练: 1.(09 年广州高三年级第一学期中段考)函数 xfy 的图象如图 2 所示.观察图象可知 函数 xfy 的定义域、值域分别是( ) A. 6,20,5 , 5,0 ;B. ,0,6,5 C. 6,20,5 , ,0 ;D. 5,2,,5 [解析] C;由图象可以看出,应选择 C 2.(09 年惠州第一次调研考)某工厂从 2000 年开始,近八年以来生产某种产品的情况是: 前四年年产量的增长速度越来越慢,后四年年产量的增长速度保持不变,则该厂这种产品的 产量 y与时间 t的函数图像可能是( ) [解析] B;前四年年产量的增长速度越来越慢,知图象的斜率随 x 的变大而变小,后四年年产量的 O-5 2 6 2 5 x y 图 2 4 8 y o t 4 8 y o t 4 8 y o t 4 8 y o t C DA B 增长速度保持不变,知图象的斜率不变,∴选 B. 3.(2004·湖南改编)设函数 2 , 0,( ) 2, 0. x bx c xf x x 若 )0()3( ff , 2)1( f ,则关于 x的 方程 xxf )( 的解的个数为 [解析] 3;由 )0()3( ff , 2)1( f 可得 0,3 cb ,从而方程 xxf )( 等价于 2)( 0 xfx x 或 xxx x 3 0 2 ,解 xxx x 3 0 2 得到 0x 或 2x ,从而得方程 xxf )( 的解 的个数为 3 4.(05 江苏)已知 ba, 为常数,若 34)( 2 xxxf , 2410)( 2 xxbaxf ,则 ba 5 = [解析] 2;因为 34)( 2 xxxf ,所以 )34()42(3)(4)()( 2222 bbxaabxabaxbaxbaxf 又 2410)( 2 xxbaxf ,所以, 2434 1042 1 2 2 bb aab a 解得 3 1 b a 或 7 1 b a ,所以 25 ba 5.对 ,、 Rba 记 bab baa baxm , , ,a ,函数 )(cos,sina)( Rxxxxmxf 的最小值是( ) A. 1 ;B. 2 2 ;C. 2 2 ;D.1 [解析] C;作出 xxf sin)( 和 xxg cos)( 的图象即可得到函数 )(cos,sina)( Rxxxxmxf 的最小值是 2 2 6.(中山市 09 届高三统测)已知函数 )( )( )( 2 1 xf xf xf ]1, 2 1[ ) 2 1,0[ x x 其中 1) 2 1(2)( 2 1 xxf , 22)(2 xxf 。作出函数 )(xf 的图象; [解析] 函数 )(xf 图象如下: 说明:图象过 2 1,0 、 1, 2 1 、 0,1 点;在区间 2 1,0 上的图象为上凸的曲线段;在区间 1, 2 1 上的图象为直线段 综合提高训练: 7.(09 年惠州第二次调研考)如图,动点 P在正方体 1 1 1 1ABCD ABC D 的对角线 1BD 上.过点 P 作垂直于平面 1 1BB D D的直线,与正方体表面相交于M N, .设 BP x ,MN y ,则函数 ( )y f x 的图象大致是( ) [解析] B;过点 P 作垂直于平面 1 1BB D D的直线,当点 P 运动时,线与正方体表面相交于M N, 两 点形成的轨迹为平行四边形,可以看出 x与 y 的变化趋势是先递增 再递减,并 且在 x的中点值时 y 取最大 8.(06 重庆)如图所示,单位圆中 BA 的长为 x, ( )f x 表示弧 BA 与弦 AB 所 围成的弓形面积的 2 倍,则函数 ( )y f x 的图像是( ) [解析] D; 如 图 所 示,单位 圆中 AB 的 长 为 x , ( )f x 表示弧 AB与弦 AB 所围成的弓形面积的 2 倍,当AB的长小于半圆时,函数 ( )y f x 的值增加的越来越 快,当AB的长大于半圆时,函数 ( )y f x 的值增加的越来越慢,所以函数 ( )y f x 的图像是 D. 9.(06 福建)已知 ( )f x 是二次函数,不等式 ( ) 0f x 的解集是 (0,5),且 ( )f x 在区间 1,4 上的 最大值是 12。 (I)求 ( )f x 的解析式; (II)是否存在实数 ,m 使得方程 37( ) 0f x x 在区间 ( , 1)m m 内有且只有两个不等的实数 根?若存在,求出m的取值范围;若不存在,说明理由。 [解析](I) ( )f x 是二次函数,且 ( ) 0f x 的解集是 (0,5), A B CD M NP A1 B1 C1 D1 y x A. O y x B. O y x C. O y x D. O 可设 ( ) ( 5)( 0).f x ax x a ( )f x 在区间 1,4 上的最大值是 ( 1) 6 .f a ,由已知,得6 12,a 2 2, ( ) 2 ( 5) 2 10 ( ). a f x x x x x x R (II)方程 37( ) 0f x x 等价于方程 3 22 10 37 0.x x 设 3 2( ) 2 10 37,h x x x 则 2'( ) 6 20 2 (3 10).h x x x x x 当 10(0, ) 3 x 时, '( ) 0, ( )h x h x 是减函数; 当 10( , ) 3 x 时, '( ) 0, ( )h x h x 是增函数。 10 1(3) 1 0, ( ) 0, (4) 5 0, 3 27 h h h 方程 ( ) 0h x 在区间 10 10(3, ), ( , 4) 3 3 内分别有惟一实数根,而在区间 (0,3), (4, ) 内没有实数 根, 所以存在惟一的自然数 3,m 使得方程 37( ) 0f x x 在区间 ( , 1)m m 内有且只有两个不同的实 数根。 第 4 讲 函数的单调性与最值 ★知识梳理 函数的单调性定义: 设函数 )(xfy 的定义域为 A,区间 AI 如果对于区间 I 内的任意两个值 1x , 2x ,当 21 xx 时,都有 )()( 21 xfxf ,那么就说 )(xfy 在区间 I 上是单调增函数, I 称为 )(xfy 的单调增区间 如果对于区间 I 内的任意两个值 1x , 2x ,当 21 xx 时,都有 )()( 21 xfxf ,那么就说 )(xfy 在区间 I 上是单调减函数, I 称为 )(xfy 的单调减区间 如果用导数的语言来,那就是: 设函数 )(xfy ,如果在某区间 I 上 0)( xf ,那么 )(xf 为区间 I 上的增函数; 如果在某区间 I 上 0)( xf ,那么 )(xf 为区间 I 上的减函数; 1.函数的最大(小)值 设函数 )(xfy 的定义域为 A 如果存在定值 Ax 0 ,使得对于任意 Ax ,有 )()( 0xfxf 恒成立,那么称 )( 0xf 为 )(xfy 的最大值; 如果存在定值 Ax 0 ,使得对于任意 Ax ,有 )()( 0xfxf 恒成立,那么称 )( 0xf 为 )(xfy 的最小值。 ★重、难点突破 重点:掌握求函数的单调性与最值的方法 难点:函数单调性的理解,尤其用导数来研究函数的单调性与最值 重难点:1.对函数单调性的理解 (1) 函数的单调性只能在函数的定义域内来讨论,所以求函数的单调区间,必须 先求函数的定义域; (2)函数单调性定义中的 1x , 2x 有三个特征:一是任意性;二是大小,即 )( 2121 xxxx ;三是同属于一个单调区间,三者缺一不可; (3)若用导数工具研究函数的单调性,则在某区间 I 上 0)( xf ( 0)( xf )仅是 )(xf 为区间 I 上的增函数(减函数)的充分不必要条件。 (4)关于函数的单调性的证明,如果用定义证明 )(xfy 在某区间 I 上的单 调性,那么就要用严格的四个步骤,即①取值;②作差;③判号;④下结论。但是要注意,不能用 区间 I 上的两个特殊值来代替。而要证明 )(xfy 在某区间 I 上不是单调递增的,只要举出反例就 可以了,即只要找到区间 I 上两个特殊的 1x , 2x ,若 21 xx ,有 )()( 21 xfxf 即可。如果用导 数证明 )(xfy 在某区间 I 上递增或递减,那么就证明在某区间 I 上 0)( xf 或 0)( xf 。 (5)函数的单调性是对某个区间而言的,所以受到区间的限制,如函数 x y 1 分别在 )0,( 和 ),0( 内都是单调递减的,但是不能说它在整个定义域即 ),0()0,( 内是单调递减的,只能 说函数 x y 1 的单调递减区间为 )0,( 和 ),0( (6)一些单调性的判断规则:①若 )(xf 与 )(xg 在定义域内都是增函数(减函数),那么 )()( xgxf 在其公共定义域内是增函数(减函数)。②复合函数的单调性规则是“异减同增” 2.函数的最值的求法 (1)若函数是二次函数或可化为二次函数型的函数,常用配方法。 (2)利用函数的单调性求最值:先判断函数在给定区间上的单调性,然后利用函数的单调性求最 值。 (3)基本不等式法:当函数是分式形式且分子分母不同次时常用此法(但有注意等号是否取得)。 (4)导数法:当函数比较复杂时,一般采用此法 (5)数形结合法:画出函数图象,找出坐标的范围或分析条件的几何意义,在图上找其变化范围。 ★热点考点题型探析 考点 1 函数的单调性 题型 1:讨论函数的单调性 [例 1] (2008 广东)设 Rk ,函数 1,1 ,1, 1 1 )( xx x xxf RxkxxfxF ,)()( . 试讨论函数 )(xF 的单调性. [解题思路]分段函数要分段处理,由于每一段都是基本初等函数的复合函数,所以应该用导数来研 究。 [解析]: 因为 1,1 ,1, 1 1 )( xx x xxf ,所以 Rx kxx kx xkxxfxF , 1 1 1 )()( . (1)当 x<1 时,1-x>0, )1(, )1( 1)( 2 xk x xF ①当 0k 时, 0)( xF 在 )1,( 上恒成立,故 F(x)在区间 )1,( 上单调递增; ②当 0k 时,令 )1(,0 )1( 1)( 2 xk x xF ,解得 k kx 1 , 且当 k kx 1 时, 0)( xF ;当 11 x k k 时, 0)( xF 故 F(x)在区间 )1,( k k 上单调递减,在区间 )1,1( k k 上单调递增; (2)当 x>1 时, x-1>0, )1(, 12 1)( xk x xF ①当 0k 时, 0)( xF 在 ),1( 上恒成立,故 F(x)在区间 ),1( 上单调递减; ②当 0k 时,令 )1(,0 12 1)( xk x xF ,解得 24 11 k x , 且当 24 111 k x 时, 0)( xF ;当 24 11 k x 时, 0)( xF 故 F(x)在区间 ) 4 11,1( 2k 上单调递减,在区间 ), 4 11( 2 k 上单调递增; 综上得,①当 k=0 时,F(x)在区间 )1,( 上单调递增,F(x)在区间 ),1( 上单调递减; ②当 k<0 时,F(x)在区间 )1,( 上单调递增,在区间 ) 4 11,1( 2k 上单调递减,在区间 ), 4 11( 2 k 上单调递增;③当 0k 时,F(x)在区间 )1,( k k 上单调递减,在区间 )1,1( k k 上单调递增,在区间 ),1( 上单调递减. 【名师指引】求函数的单调区间或研究函数的单调性是高考的一个热点,分段落函数用注意分段处 理. 题型 2:研究抽象函数的单调性 [例 2] 定义在 R 上的函数 )(xfy , 0)0( f ,当 x>0 时, 1)( xf ,且对任意的 a、b∈R, 有 f(a+b)=f(a)·f(b). (1)求证:f(0)=1; (2)求证:对任意的 x∈R,恒有 f(x)>0; (3)求证:f(x)是 R 上的增函数; (4)若 f(x)·f(2x-x2)>1,求 x的取值范围. [解题思路]抽象函数问题要充分利用“恒成立”进行“赋值”,从关键等式和不等式的特点入手。 [解析](1)证明:令 a=b=0,则 f(0)=f 2(0). 又 f(0)≠0,∴f(0)=1. (2)证明:当 x<0 时,-x>0, ∴f(0)=f(x)·f(-x)=1. ∴f(-x)= )( 1 xf >0.又 x≥0 时 f(x)≥1>0, ∴x∈R 时,恒有 f(x)>0. (3)证明:设 x1<x2,则 x2-x1>0. ∴f(x2)=f(x2-x1+x1)=f(x2-x1)·f(x1). ∵x2-x1>0,∴f(x2-x1)>1. 又 f(x1)>0,∴f(x2-x1)·f(x1)>f(x1). ∴f(x2)>f(x1).∴f(x)是 R 上的增函数. (4)解:由 f(x)·f(2x-x2)>1,f(0)=1 得 f(3x-x2)>f(0).又 f(x)是 R 上的增函 数, ∴3x-x2>0.∴0<x<3. 【名师指引】解本题的关键是灵活应用题目条件,尤其是(3)中“f(x2)=f[(x2-x1)+x1]”是证 明单调性的关键,这里体现了向条件化归的策略. [新题导练] 1.(珠海北大希望之星实验学校 09 届高三)函数 2 2log 4f x x x 的单调递减区间是( ) A. (0, 4) ; B. (0, 2) ; C. (2, 4) ; D. (2, ) [解析] C;由 04 2 xx 得 40 x ,又由 4)2(4 22 xxxu 知函数u在 )4,2( 上是减 函数,根据复合函数的单调性知函数 2 2log 4f x x x 的单调递减区间是 )4,2( 2.(东皖高级中学 09 届高三月考)函数 2 1 2 log ( 5 6)y x x 的单调增区间为( ) A. 5 2 , ;B. (3 ), ;C. 5 2 , ;D. ( 2), [解析] D;由 0652 xx 得 2x 或 3x ,又函数 4 1) 2 5(65 22 xxxu 在 ( 2), 上是减函数, uy 2 1log 在 ),0( 上是减函数,所以函数 2 1 2 log ( 5 6)y x x 的单调增区间为 ( 2), 3. (2008 全国Ⅰ卷)已知函数 3 2( ) 1f x x ax x ,aR . (Ⅰ)讨论函数 ( )f x 的单调区间; (Ⅱ)设函数 ( )f x 在区间 2 1 3 3 , 内是减函数,求 a的取值范围. [解析] (1) 3 2( ) 1f x x ax x ;(2) 7 4 a≥ (1) 3 2( ) 1f x x ax x 求导: 2( ) 3 2 1f x x ax 当 2 3a ≤ 时, 0≤ , ( ) 0f x ≥ , ( )f x 在R 上递增 当 2 3a , ( ) 0f x 求得两根为 2 3 3 a ax 即 ( )f x 在 2 3 3 a a , 递增, 2 23 3 3 3 a a a a , 递减, 2 3 3 a a , 递增 (2) 2 2 3 2 3 3 3 1 3 3 a a a a ≤ ≥ ,且 2 3a 解得: 7 4 a≥ 考点 2 函数的值域(最值)的求法 题型 1:求分式函数的最值 [例 3] (2000 年上海)已知函数 x axxxf 2)( 2 ).,1[, x 当 2 1 a 时,求函数 )(xf 的最小值; [解题思路]当 2 1 a 时, 2 2 1)( x xxf ,这是典型的“对钩函数”,欲求其最小值,可以考虑 均值不等式或导数; [解析]当 2 1 a 时, 22 11)(',2 2 1)( x xf x xxf 1x , 0)( xf 。 )(xf 在区间 ),1[ 上为增函数。 )(xf 在区间 ),1[ 上的最小值为 2 7)1( f 。 【名师指引】对于函数 ,2 2 1)( x xxf 若 0x ,则优先考虑用均值不等式求最小值,但要注意 等号是否成立,否则会得到 222 2 122) 2 1()( x x x xxf 而认为其最小值为 22 ,但实际上,要取得等号,必须使得 x x 2 1 ,这时 ), 2 1[ x 所以,用均值不等式来求最值时,必须注意:一正、二定、三相等,缺一不可。其次,不等式恒成 立问题常转化为求函数的最值。本题考查求函数的最小值的三种通法:利用均值不等式,利用函数 单调性,二次函数的配方法,考查不等式恒成立问题以及转化化归思想; 题型 2:利用函数的最值求参数的取值范围 [例 4] (2000 年上海)已知函数 x axxxf 2)( 2 ).,1[, x 若对任意 [1, ), ( ) 0x f x 恒成立,试求实数 a的取值范围。 [解题思路] 欲求参数 a的取值范围,应从 [1, ), ( ) 0x f x 恒成立的具体情况开始。 [解析] 02)( 2 x axxxf 在区间 ),1[ 上恒成立; 022 axx 在区间 ),1[ 上恒成立; axx 22 在区间 ),1[ 上恒成立; 函数 xxy 22 在区间 ),1[ 上的最小值为 3, 3 a 即 3a 【名师指引】这里利用了分离参数的方法,将问题转化为求函数的最值。 题型 3:求三次多项式函数的最值 [例 5](09 年高州中学)已知 a为实数,函数 ))(1()( 2 axxxf ,若 0)1(' f ,求函数 )(xfy 在 3[ ,1] 2 上的最大值和最小值。 [解题思路]求三次多项式函数在闭区间上的最值,应该用导数作为工具来研究其单调性。 [解析]∵ 123)(,)(0)1( 223 axxxfaxaxxxff ,由, , ,2,0123 aa ……………………3 分 143)( 2 xxxf ……………………4 分 )1)( 3 1(3)( xxxf由 得: 当 3 110)( xxxf 或时, ……………………5 分 当 3 110)( xxf 时, ……………………6 分 因此, )(xf 在区间 ]1, 3 1[]1, 2 3[ 和 内单调递减,而在 ] 3 1,1[ 内单调递减, 且 27 50) 3 1()(,2)1()( fxffxf 极小值极大值 又 8 13) 2 3( f 8 13 27 50,6)1( 且f , 8 13) 2 3(,6)1(]1, 2 3[)( ffxf 最小值上的最大值在 ,………………10 分 【名师指引】用导数来研究其单调性和最值是高考考查的重点和热点,同时也是难点,要求考生熟 练掌握用导数来研究其单调性和最值的方法和步骤。 [新题导练] 4.(09 年广东南海)若函数 2 13 ln( ) 1 xy x x 2 1, 2 1x 的最大值与最小值分别为 M,m,则 M+m = [解析] 6;由 )]1ln()1[ln() 1 1ln()( 22 xxx x xxxf 知 )(xf 在 ] 2 1,0[ 上是增函数 又因为函数 ) 1 1ln()( 2 x xxxf 是奇函数,所以函数 2 13 ln( ) 1 xy x x 2 1, 2 1x 是增函数,故 M+m= 6)] 2 11 2 11 ln() 2 1(3[)] 2 11 2 11 ln() 2 1(3[ 22 5.(高州中学 09 届模拟)已知函数 )0(4)( 2 x x axxxf 。 (Ⅰ)若 )(xf 为奇函数,求 a的值; (Ⅱ)若 )(xf 在 ),3[ 上恒大于 0,求 a的取值范围。 [解析](Ⅰ) 0a ;(Ⅱ) a的取值范围为 3 13 a (Ⅰ) )(xf 的定义域关于原点对称 若 )(xf 为奇函数,则 )(4)()()( 2 xf x xaxxf ∴ 0a (Ⅱ) 2 41)( x xf ∴在 ),3[ 上 0)( xf ∴ )(xf 在 ),3[ 上单调递增 ∴ )(xf 在 ),3[ 上恒大于 0 只要 )3(f 大于 0 即可, ∴ 3 130133 aa 若 )(xf 在 ),3[ 上恒大于 0, a的取值范围为 3 13 a 备选例题:(06 年重庆)已知定义域为 R的函数 1 2( ) 2 x x bf x a 是奇函数。 (Ⅰ)求 ,a b的值; (Ⅱ)若对任意的 t R ,不等式 2 2( 2 ) (2 ) 0f t t f t k 恒成立,求 k的取值范围; [解析](Ⅰ)因为 ( )f x 是奇函数,所以 0)0( f ,即 1 1 1 20 1 ( ) 2 2 x x b b f x a a 又由 )1()1(, ff 知 111 2 2 2. 4 1 a a a (Ⅱ)[解法一]由(Ⅰ)知 1 1 2 1 1( ) 2 2 2 2 1 x x xf x ,易知 ( )f x 在 ( , ) 上 为减函数。又因 ( )f x 是奇函数,从而不等式: 2 2( 2 ) (2 ) 0f t t f t k 等价于 2 2 2( 2 ) (2 ) ( 2 )f t t f t k f k t ,因 ( )f x 为减函数,由上式推得: 2 22 2t t k t .即对一切 t R 有: 23 2 0t t k , 从而判别式 14 12 0 . 3 k k [解法二]由(Ⅰ)知 1 1 2( ) 2 2 x xf x .又由题设条件得: 2 2 2 2 2 2 2 1 2 1 1 2 1 2 0 2 2 2 2 t t t k t t t k , 即 2 2 2 22 1 2 2 1 2(2 2)(1 2 ) (2 2)(1 2 ) 0t k t t t t t k , 整理得 23 22 1,t t k 因底数2>1,故: 23 2 0t t k 上式对一切 t R 均成立,从而判别式 14 12 0 . 3 k k ★抢分频道 基础巩固训练: 1.(华师附中 09 高三数学训练题)若函数 baxxxf ||)( 2 在区间 ]0,( 上为减函数,则 实数 a的取值范围是( ) A. 0a ;B. 1a ;C. 0a ;D. 1a [ 解析 ] C ;因 为 )( )( ||)( 2 2 2 axbaxx axbaxx baxxxf ,由 其图象 知,若 函数 baxxxf ||)( 2 在区间 ]0,( 上为减函数,则应有 0a 2.(普宁市城东中学 09)若函数 3 2)( k x kxxh 在 ),1( 上是增函数,则实数 k的取值范围是 ( ) A.[ 2 , ) ;B.[2 , ) ; C. ( , 2] ;D. ( , 2] [解析] A;若函数 3 2)( k x kxxh 在 ),1( 上是增函数,则 02)( 2 x kxh 对于 ),1( x 恒成立,即 22xk 对于 ),1( x 恒成立,而函数 )),1[(2 2 xxu 的最大值为 2 ,实数 k 的取值范围是 [ 2 , ) 3.(09 汕头金中)下列四个函数中,在区间 ) 4 1,0( 上为减函数的是( ) A. x xy 2 1 ;B. xy ) 2 1( ;C. xxy 2log ;D. 3 1 xy [解析] C;显然 xy ) 2 1( 在 ) 4 1,0( 上是增函数, 3 1 xy 在 ) 4 1,0( 上也是增函数 而对 x xy 2 1 求导得 )2ln1() 2 1(2ln) 2 1() 2 1( xxy xxx ,对于 ) 4 1,0(x , 0y ,所以 x xy 2 1 在区间 ) 4 1,0( 上为增函数,从而应选择 C 4.(09 潮州金山中学)已知函数 12)( 2 xxxf ,若存在实数 t,当 mx ,1 时, xtxf )( 恒成立,则实数m的最大值是( ) A.1;B.2;C.3;D.4 [解析] D;依题意,应将函数 )(xf 向右平行移动得到 )( txf 的图象,为了使得在 m,1 上, )( txf 的图象都在直线 xy 的下方,并且让m取得最大,则应取 2t ,这时m取得最大值 4 5.(06 北京改编)已知 (3 1) 4 , 1 ( ) log , 1a a x a x f x x x 是 ( , ) 上的减函数,那么 a的取值范 围是 [解析] ) 3 1, 7 1[ ;要 xy alog 在 )1[ , 上是减函数,则 10 a ,要 axa 4)13( 在 )1,( 上 为减函数,则需 013 a 并且 041)13( aa ,所以 3 1 7 1 a 6.(2008 浙江理)已知 t 为常数,函数 txxy 22 在区间[0,3]上的最大值为 2, 则 t [解析]1;显然函数 txxy 22 的最大值只能在 1x 或 3x 时取到, 若在 1x 时取到,则 221 t ,得 1t 或 3t 1t , 3x 时, 2y ; 3t , 3x 时, 6y (舍去); 若在 3x 时取到,则 269 t ,得 1t 或 5t 1t , 1x 时, 2y ; 5t , 1x 时, 6y (舍去) 所以 1t 综合提高训练: 7.(06 陕西改编)已知函数 2( ) 2 4(0 3),f x ax ax a 若 01, 2121 axxxx 则 )(1 xf 与 )(2 xf 的大小关系为 [解析] 1 2( ) ( )f x f x ;函数 2( ) 2 4(0 3),f x ax ax a 的图象开口向上,对称轴为 1x , 因 30 a ,故 )1,2()1(21 axx ,从而 ) 2 1,1( 2 21 xx ,又 21 xx ,所以 2x 的对应点到对称轴的距离大于 1x 的对应点到对称轴的距离,故 1 2( ) ( )f x f x 8.已知函数 ) 2 1( 12 23)( x x xxf ,求 ) 2010 2009() 2010 2() 2010 1( fff 的值 [解析] 2 6027 ;为 3 1)1(2 2)1(3 12 23)1()( x x x xxfxf , 令 ) 2010 2009() 2010 2() 2010 1( fffS ,则 ) 2010 1() 2010 2008() 2010 2009( fffS , 从而 32009 )] 2010 1() 2010 2009([)] 2010 2008() 2010 2([)] 2010 2009() 2010 1([2 ffffffS 所以 2 6027) 2010 2009() 2010 2() 2010 1( fffS 9.(09 年汕头金中)对于函数 Mxfxxxf )(,2)( 2 在使 成立的所有常数 M 中,我 们把 M 的最大值-1 叫做 的下确界xxxf 2)( 2 , 且则对于 Rba, ,0, 不全为ba 2 22 )( ba ba 的下确界为( ) A. 2 1 ;B.2;C. 4 1 ;D.4 [解析] A;因为 2 1 )()(2)( 2222 22 22 22 2 22 baba ba abba ba ba ba , 故 2 22 )( ba ba 的下确界为 2 1 10.(08 年湖南)设 ][x 表示不超过 x的最大整数(如 2]2[ , 1] 4 5[ ),对于给定的 nN*,定义 ( 1) ( 1) , ( 1) ( 1) x n n n n x C x x x x x 1, , 求当 x 3 ,3 2 时,函数 xC8 的值域 [解析] ]28, 3 28(] 3 16,4( ;当 )2, 2 3[x 时, 1][ x , x C x 8 8 ,因为函数 x u 8 在 )2, 2 3[ 上是减 函数,得 3 1684 x ;当 )3,2[x 时, 2][ x , )1( 56 8 xx C x ,因为 6)1(2 xx ,由单调性 得 28 )1( 56 3 28 xx ,故当 x 3 ,3 2 时,函数 xC8 的值域是 ]28, 3 28(] 3 16,4( 第 5 讲 函数的奇偶性和周期性 ★知识梳理 1.函数的奇偶性的定义: ①对于函数 )(xf 的定义域内任意一个 x,都有 )()( xfxf 〔或 0)()( xfxf 〕,则称 )(xf 为奇函数. 奇函数的图象关于原点对称。 ②对于函数 )(xf 的定义域内任意一个 x,都有 )()( xfxf 〔或 0)()( xfxf 〕,则称 )(xf 为偶函数. 偶函数的图象关于 y 轴对称。 ③通常采用图像或定义判断函数的奇偶性. 具有奇偶性的函数,其定义域原点关于对称(也就是说, 函数为奇函数或偶函数的必要条件是其定义域关于原点对称) 3.函数的周期性命定义: 对于函数 )(xf ,如果存在一个非零常数T ,使得定义域内的每一个 x值,都满足 )()( xfTxf ,那么函数 )(xf 就叫做周期函数,非零常数T 叫做这个函数的周期。 ★重、难点突破 重点:函数的奇偶性和周期性,函数的奇偶性、单调性、周期性的综合应用 难点:函数的奇偶性的判断 函数的奇偶性与单调性、函数的奇偶性与周期性的综合应用 重难点:1.函数的奇偶性的判断:可以利用奇偶函数的定义判断或者利用定义的等价形式 )0)((1 )( )(0)()()()( xf xf xfxfxfxfxf ,也可以利用函数图象的对称性 去判断函数的奇偶性.注意①若 0)( xf ,则 )(xf 既是奇函数又是偶函数,若 )0()( mmxf ,则 )(xf 是偶函数;②若 )(xf 是奇函数且在 0x 处有定义,则 0)0( f ③若在函数 )(xf 的定义域 内有 )()( mfmf ,则可以断定 )(xf 不是偶函数,同样,若在函数 )(xf 的定义域内有 )()( mfmf ,则可以断定 )(xf 不是奇函数。 2.奇偶函数图象的对称性 (1) 若 )( xafy 是偶函数,则 )()2()()( xfxafxafxaf )(xf 的图象 关于直线 ax 对称; (2) 若 )( xbfy 是偶函数,则 )()2()()( xfxbfxbfxbf )(xf 的图象关于点 )0,(b 中心对称; 3.函数的周期性 周期性不仅仅是三角函数的专利,抽象函数的周期性是高考热点,主要难点是 抽象函数周期的发现,主要有几种情况: (1)函数值之和等于零型,即函数 )(0)()( baxbfxaf 对于定义域中任意 x满足 )(0)()( baxbfxaf ,则有 )()]22([ xfabxf ,故函数 )(xf 的周期是 )(2 abT (2)函数图象有 ax , )( babx 两条对称轴型 函数图象有 ax , )( babx 两条对称轴,即 )()( xafxaf , )()( xbfxbf ,从而得 )()]22([ xfabxf , 故函数 )(xf 的周期是 )(2 abT (3) 两个函数值之积等于 1 ,即函数值互为倒数或负倒数型 若 )(1)()( babxfaxf ,则得 )]22()2[()2( abaxfaxf ,所以函数 )(xf 的 周期是 abT 22 ;同理若 )(1)()( babxfaxf ,则 )(xf 的周期是 )(2 abT (4) 分式递推型,即函数 )(xf 满足 )( )(1 )(1)( ba bxf bxfaxf 由 )( )(1 )(1)( ba bxf bxfaxf 得 )2( 1)2( bxf axf ,进而得 1)2()2( bxfaxf ,由前面的结论得 )(xf 的周期是 )(4 abT ★热点考点题型探析 考点 1 判断函数的奇偶性及其应用 题型 1:判断有解析式的函数的奇偶性 [例 1] 判断下列函数的奇偶性: (1)f(x)=|x+1|-|x-1|;(2)f(x)=(x-1)· x x 1 1 ; (3) 2|2| 1)( 2 x xxf ;(4) ).0()1( ),0()1( )( xxx xxx xf [思路点拨]判断函数的奇偶性应依照定义解决,但都要先考查函数的定义域。 [解析] (1)函数的定义域 x∈(-∞,+∞),对称于原点. ∵f(-x)=|-x+1|-|-x-1|=|x-1|-|x+1|=-(|x+1|-|x-1|)=-f(x), ∴f(x)=|x+1|-|x-1|是奇函数. (2)先确定函数的定义域.由 x x 1 1 ≥0,得-1≤x<1,其定义域不对称于原点,所以 f(x)既不是 奇函数也不是偶函数. (3)去掉绝对值符号,根据定义判断. 由 ,02|2| ,01 2 x x 得 .40 ,11 xx x 且 故 f(x)的定义域为[-1,0)∪(0,1],关于原点对称,且有 x+2>0. 从而有 f(x)= 22 1 2 x x = x x 21 ,∴f(-x)= x x 2)(1 =- x x 21 =-f(x) 故 f(x)为奇函数. (4)∵函数 f(x)的定义域是(-∞,0)∪(0,+∞),并且当 x>0 时,-x<0, ∴f(-x)=(-x)[1-(-x)]=-x(1+x)=-f(x)(x>0). 当 x<0 时,-x>0,∴f(-x)=-x(1-x)=-f(x)(x<0). 故函数 f(x)为奇函数. 【名师指引】○1 函数的奇偶性是函数的一个整体性质, 定义域具有对称性 ( 即若奇函数或偶函数的 定义域为 D, 则 Dx 时 Dx ) 是一个函数为奇函数或偶函数的必要条件 ○2 分段函数的奇偶性一般要分段证明.③判断函数的奇偶性应先求定义域再化简函数解析式. 题型 2:证明抽象函数的奇偶性 [例 2] (09 年山东梁山)定义在区间 )1,1( 上的函数 f (x)满足:对任意的 )1,1(, yx , 都有 ) 1 ()()( xy yxfyfxf . 求证 f (x)为奇函数; [思路点拨]欲证明 )(xf 为奇函数,就要证明 )()( xfxf ,但这是抽象函数,应设法充 分利用条件“对任意的 )1,1(, yx ,都有 ) 1 ()()( xy yxfyfxf ”中的 yx, 进行合理 “赋值” [解析]令 x = y = 0,则 f (0) + f (0) = )0() 01 00( ff ∴ f (0) = 0 令 x∈(-1, 1) ∴-x∈(-1, 1) ∴ f (x) + f (-x) = f ( 21 x xx ) = f (0) = 0 ∴ f (-x) =-f (x) ∴ f (x) 在(-1,1)上为奇函数 【名师指引】对于抽象函数的奇偶性问题,解决的关键是巧妙进行“赋值”,而抽象函数的不等式 问题,要灵活利用已知条件,尤其是 f (x1) -f (x2) = f (x1) + f (-x2) [新题导练] 1.(09 广东电白一中)设函数 axxxf 12 为奇函数,则 a ___________。 [解析]0;由函数 axxxf 12 为奇函数得到 00 f ,即 00102 a 所以 0a 2.(高州中学 09 届训练题)已知函数 babxaxxf 3)( 2 是定义域为 ]2,1[ aa 的偶函数, 则 ba 的值是( ) A.0;B. 3 1 ;C.1;D. 1 [解析 ]B;由函数 babxaxxf 3)( 2 是定义域为 ]2,1[ aa 的偶函数得 0b ,并且 aa 21 ,即 3 1 a ,所以 ba 的值是 0 3.定义两种运算: 22 baba , 2)( baba ,则 2)2( 2)( x xxf 是______________函数,(填奇、偶、非奇非偶,既奇又偶四个中的一个) [解析]奇;依 22 baba 和 2)( baba 得 22 4 2)2( 4 2)2( 2)( 2 2 2 x x x x x xxf ,其定义域为 ]2,0()0,2[ ,所以 x x x xxf 22 4 2)2( 4)( ,可见, )(xf 是奇函数 4.已知函数 cbx axxf 1)( 2 (a、b、c∈Z)是奇函数,又 2)1( f , 3)2( f ,求 a、b、c的值. [解析] 011 cba ,, ;由 f(-x)=-f(x),得-bx+c=-(bx+c). ∴c=0,由 f(1)=2,得 a+1=2b,由 f(2)<3,得 1 14 a a <3, 解得-1<a<2.又 a∈Z,∴a=0 或 a=1.若 a=0,则 b= 2 1 ,与 b∈Z 矛盾.∴a=1,b=1,c=0. 考点 2 函数奇偶性、单调性的综合应用 [ 例 3] ( 普 宁 市 城 东 中 学 09 ) 已 知 奇 函 数 )(xf 是 定 义 在 )2,2( 上 的 减 函 数 , 若 0)12()1( mfmf ,求实数m的取值范围。 [思路点拨]欲求m的取值范围,就要建立关于m的不等式,可见,只有从 0)12()1( mfmf 出发,所以应该利用 )(xf 的奇偶性和单调性将外衣“ f ”脱去。 [解析] )(xf 是定义在 )2,2( 上奇函数 对任意 x )2,2( 有 f x f x 由条件 0)12()1( mfmf 得 ( 1) (2 1)f m f m = (1 2 )f m )(xf 是定义在 )2,2( 上减函数 2 1 2 1 2m m ,解得 1 2 2 3 m 实数m的取值范围是 1 2 2 3 m 【名师指引】利用函数的奇偶性可以求对称区间上的函数的表达式 [例 4]设函数 f(x)是定义在 R 上的偶函数,并在区间(-∞,0)内单调递增,f(2a2+a+1)查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档