【2020年高考数学预测题、估测题】天津市试卷(文史类)5【附详细答案和解析_可编辑】
【2020年高考数学预测题、估测题】天津市试卷(文史类)5【附详细答案和解析 可编辑】
真水无香陈 tougao33
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 5 分 ,共计50分 , )
1. 已知:P={x|2x≥1},Q={x|log2 x≥1},则P∩∁RQ=( )
A.[2,+∞) B.[0,2) C.[0,2] D.[0,+∞)
2. 若x,y满足约束条件x+y-1≥0,x-y+1≥0,3x-y-3≤0,则目标函数z=x-3y的最小值为( )
A.-2 B.1 C.-7 D.-3
3. 有下面四个命题,其中正确命题的序号是( )
①“直线a、b不相交”是“直线a、b为异面直线”的充分而不必要条件;
②“直线 l⊥ 平面α内所有直线”的充要条件是“ l⊥ 平面α”;
③“直线 a// 直线b”的充要条件是“a平行于b所在的平面”;
④“直线 a// 平面α”的必要而不充分条件是“直线a平行于α内的一条直线."
A.①③ B.②③ C.②④ D.③④
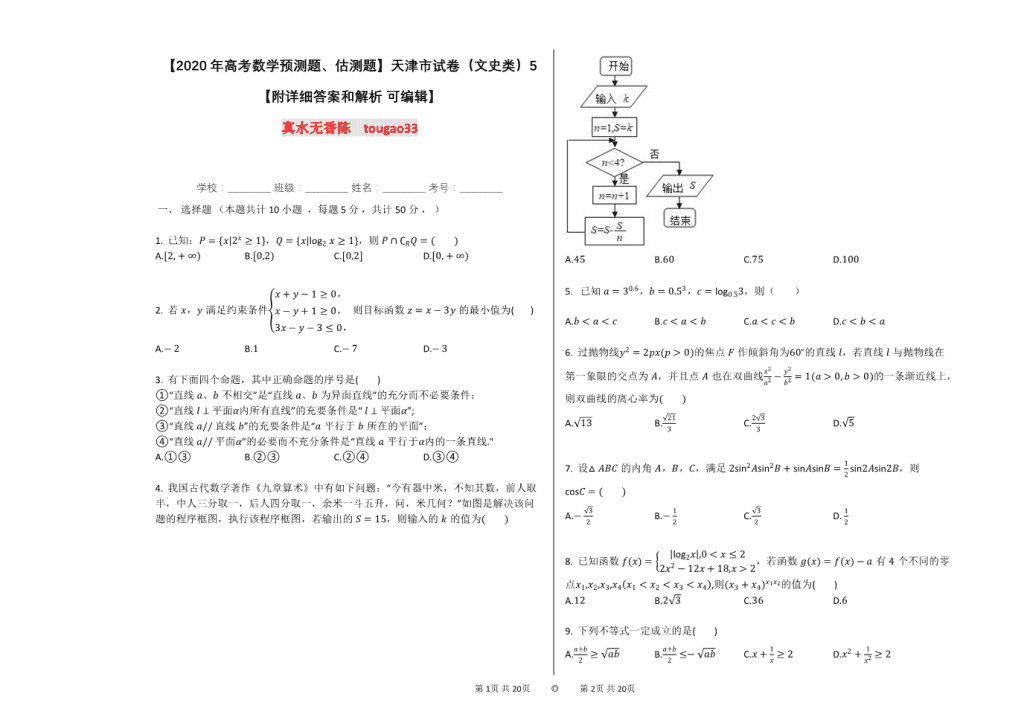
4. 我国古代数学著作《九章算术》中有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升,问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=15,则输入的k的值为( )
A.45 B.60 C.75 D.100
5. 已知a=30.6,b=0.53,c=log0.53,则( )
A.b
0)的焦点F作倾斜角为60∘的直线l,若直线l与抛物线在第一象限的交点为A,并且点A也在双曲线x2a2-y2b2=1(a>0, b>0)的一条渐近线上,则双曲线的离心率为( )
A.13 B.213 C.233 D.5
7. 设△ABC的内角A,B,C,满足2sin2Asin2B+sinAsinB=12sin2Asin2B,则cosC=( )
A.-32 B.-12 C.32 D. 12
8. 已知函数f(x)=log2x,02,若函数g(x)=f(x)-a有4个不同的零点x1,x2,x3,x4x10.当m=3时解此不等式________;
13. 函数f(x)=xcosx+sinθ在(0, 0)处的切线方程为________.
14. 一个正三棱柱的侧面展开图是一个边长为6cm的正方形,则它的体积为________.
三、 解答题 (本题共计 6 小题 ,每题 12 分 ,共计72分 , )
15.
某节目邀请全国各年龄段、各个领域的诗词爱好者共同参与诗词知识比拼,“百人团”由一百多位来自全国各地的选手组成,其人数按照年龄分组统计如表:
年龄/岁
[7,20)
[20,40)
[40,80]
频数
18
54
36
(1)用分层抽样的方法从“百人团”中抽取人参加挑战,求从这三个不同年龄组中分别抽取的挑战者人数;
(2)从(1)中抽取的6人中任选2人参加一对一的对抗比赛,求这2人来自同一年龄组的概率.
16. 在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB=35.
(1)求b和sinA的值;
(2)求sin(2A+π4)的值.
17. 如图,四边形ADEF为正方形,四边形ABCD为梯形,且AF⊥面ABCD,AD⊥CD,AB // CD,AB=AD=2,CD=4,M为CE的中点.
(1)求证:BM // 平面ADEF;
(2)求证:BC⊥平面BDE,并求直线CE与平面BDE所成角的正弦值.
18. 已知在等比数列{an}中,a2=2,a4a5=128,数列{bn}满足b1=1,b2=2,且{bn+12an}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
19. 如图,已知抛物线x2=y,点A(-12, 14),B(32, 94),抛物线上的点P(x, y)(-120 时,求证:函数 Fx 有两个不同的零点 x1,x2x1<x2,且 x2-x12或x<-1}
【解答】
解:当m=3时,
不等式x2-x-2>0,
解得:{x|x>2或x<-1}.
故答案为:{x|x>2或x<-1}.
13.【答案】
x-y=0
【解答】
由f(x)=xcosx+sinθ,得f'(x)=cosx-xsinx,
∴ f'(0)=(1)
又f(0)=sinθ=0,
∴ 函数f(x)=xcosx+sinθ在(0, 0)处的切线方程为y-0=1×(x-0),
即x-y=(0)
故答案为:x-y=(0)
14.【答案】
63cm3
【解答】
解:将一个边长为6cm的正方形卷成一个底面为正三角形的三棱柱,
底面边长为2cm,底面面积为:32×2=3cm2,
所以此三棱柱的体积为3×6=63cm3.
故答案为:63cm3.
三、 解答题 (本题共计 6 小题 ,每题 12 分 ,共计72分 )
15.【答案】
解:(1)因为样本容量与总体个数比是6108=118,所以从[7,20)年龄组抽取的挑战者人数为118×18=1,从[20,40)年龄组抽取的挑战者人数为118×54=3,从[40,80]年龄组抽取的挑战者人数为118×36=2.因此在[7,20),[20,40),[40,80]这三个不同年龄组中抽取的挑战者人数分别为1,3,2.
(2)记从[7,20)年龄组中抽取的1人为a,从[20,40)年龄组中抽取的3人分别为b,c,d,从[40,80]年龄组中抽取的2人分别为e,f.从这6人中任取2人构成的所有基本事件有(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),
(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15个.因为每人被抽到的机会均等,因此这些基本事件的出现是等可能的,记事件A为“2人来自同一年龄组”,包含(b,c),(b,d),(c,d),(e,f),共4个基本事件,则P(A)=415,故这2人来自同一年龄组的概率为415.
【解答】
解:(1)因为样本容量与总体个数比是6108=118,所以从[7,20)年龄组抽取的挑战者人数为118×18=1,从[20,40)年龄组抽取的挑战者人数为118×54=3,从[40,80]年龄组抽取的挑战者人数为118×36=2.因此在[7,20),[20,40),[40,80]这三个不同年龄组中抽取的挑战者人数分别为1,3,2.
(2)记从[7,20)年龄组中抽取的1人为a,从[20,40)年龄组中抽取的3人分别为b,c,d,从[40,80]年龄组中抽取的2人分别为e,f.从这6人中任取2人构成的所有基本事件有(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),
(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15个.因为每人被抽到的机会均等,因此这些基本事件的出现是等可能的,记事件A为“2人来自同一年龄组”,包含(b,c),(b,d),(c,d),(e,f),共4个基本事件,则P(A)=415,故这2人来自同一年龄组的概率为415.
16.【答案】
解:(1)在△ABC中,因为a>b,
故由sinB=35,可得cosB=45.
由已知及余弦定理,
得b2=a2+c2-2accosB=13.
所以b=13.
由正弦定理asinA=bsinB
第17页 共20页 ◎ 第18页 共20页
,
得sinA=asinBb=31313.
(2)由(1)及ab,
故由sinB=35,可得cosB=45.
由已知及余弦定理,
得b2=a2+c2-2accosB=13.
所以b=13.
由正弦定理asinA=bsinB,
得sinA=asinBb=31313.
(2)由(1)及a0,当120,当120时,fxmax=f1a=ln1a-1+a ,
令其为 ga,则 g'a=a-1a.
所以g(a)在(0, 1)上单调递减,在(1, +∞)上单调递增,
又因为 g1=0 ,
所以 a=1.
(2)∵ F(x)=m(x-1)lnx-lnx+x-3e,
F'(x)=m(lnx+1+-1x)-1x+1,
∴ F″(x)=mx+m+1x2>0,
∴ F'(x)单调递增,
又∵ F'(1)=0,
∴ F(x)在(0, 1)上单调递减,在(1, +∞)上单调递增,
又∵ F(1)<0,
∴ 存在x1∈(0, 1),x2∈(1, +∞),
又∵ F(1e)=m(1-1e)+1-2e>0,
F(e)=m(e-1)+e2-e-3e>0,
∴ x1>1e
第17页 共20页 ◎ 第18页 共20页
,x20时,fxmax=f1a=ln1a-1+a ,
令其为 ga,则 g'a=a-1a.
所以g(a)在(0, 1)上单调递减,在(1, +∞)上单调递增,
又因为 g1=0 ,
所以 a=1.
(2)∵ F(x)=m(x-1)lnx-lnx+x-3e,
F'(x)=m(lnx+1+-1x)-1x+1,
∴ F″(x)=mx+m+1x2>0,
∴ F'(x)单调递增,
又∵ F'(1)=0,
∴ F(x)在(0, 1)上单调递减,在(1, +∞)上单调递增,
又∵ F(1)<0,
∴ 存在x1∈(0, 1),x2∈(1, +∞),
又∵ F(1e)=m(1-1e)+1-2e>0,
F(e)=m(e-1)+e2-e-3e>0,
∴ x1>1e,x2
查看更多