- 2021-04-23 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2009年中考咸宁数学试题
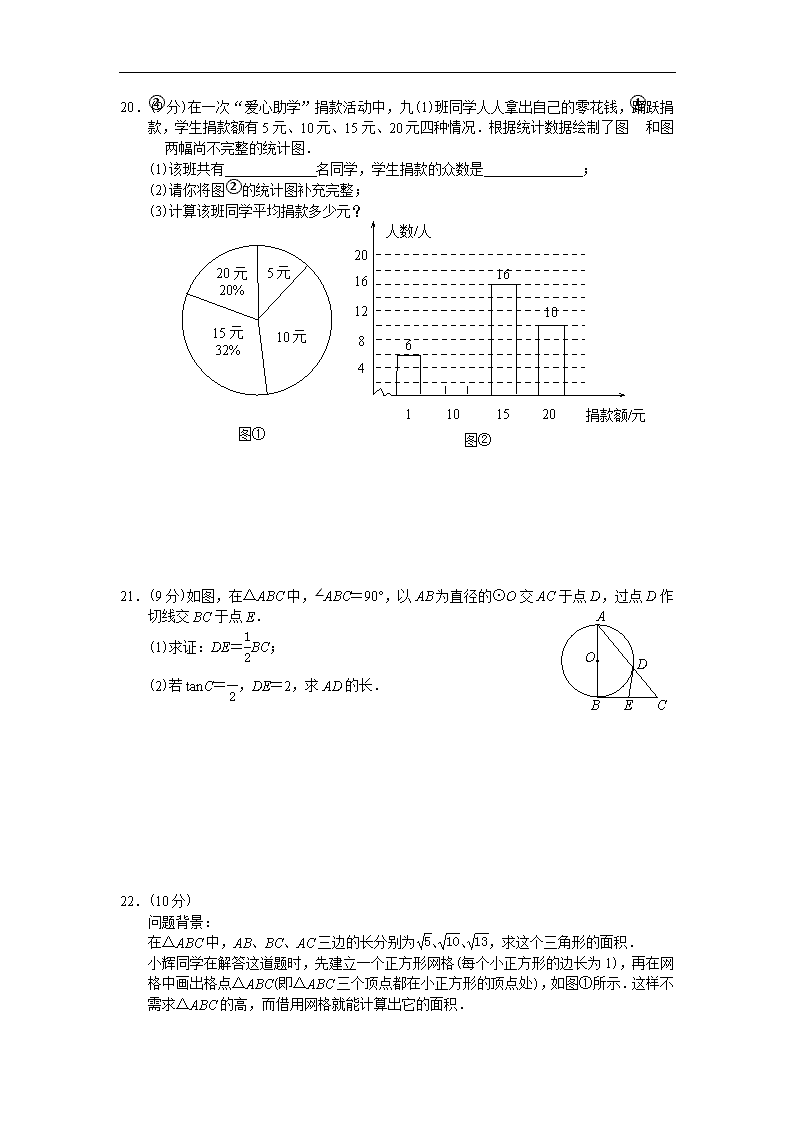
2009年中考咸宁数学试题 一、精心选一选(本大题共8小题,每小题3分,满分24分) 1.-4的绝对值是( ) A.-4 B.- C.4 D. 2.5月18日某地的最低气温是11℃,最高气温是27℃.下面用数轴表示这一天气温变化范围正确的是( ) 3.下列运算正确的是( ) A.x2+x3=x5 B.(x2)3=x6 C.(x-2)2=x2-4 D.x·x-1=0 4.温家宝总理在2009年政府工作报告中提出,今后三年内各级政府拟投入医疗卫生领域的资金将达到8500亿元人民币.用科学记数表表示“8500亿”为( ) A.85×1010 B.8.5×1010 C.8.5×1011 D.0.85×1012 5.方程3x(x+1)=3x+3的解为( ) A.x=1 B.x=-1 C.x1=0,x2=-1 D.x1=1,x2=-1 6.下列说法正确的是( ) A.某一种彩票中奖概率是,那么买1000张这种彩票就一定能中奖 B.打开电视机看CCTV—5频道,正在播放NBA篮球比赛是必然发生的事件 A O M N y x C.调查某池塘中现有鱼的数量,宜采用抽样调查 D.极差不能反映数据的波动情况 7.如图,在平面直角坐标系中,⊙A与y轴相切于原点O, 平行于x轴的直线交⊙A于M、N两点,若点M的坐标 是(-4,-2),则点N的坐标为( ) A.(-1,-2) B.(1,-2) C.(-1.5,-2) D.(1.5,-2) 8.如图,桌面上的模型由20个棱长为a的小正方体组成,现将该模型 露在外面的部分涂上涂料,则涂上涂料部分的总面积为( ) A.20a2 B.30a2 C.40a2 D.50a2 二、细心填一填(本大题共8小题,每小题3分,满分24分) 9.函数y=中,自变量x的取值范围是 . 10.分式方程=的解是 . 11.同时两枚硬币,掷两枚硬币全部正面朝上的概率为 . 12.已知A、B是抛物线y=x2-4x+3上位置不同的两点,且关于抛物线的对称轴对称,则点A、B的坐标可能是_____________(写出一对即可). 13.为了庆祝祖国六十华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB、AC夹角为120º,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为____________cm2(取3). 14.如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,……第2009次输出的结果为___________. 输入x x x+3 输出 x为偶数 x为奇数 A B C D E 15.反比例函数y1=与一次函数y2=-x+b的图象交于点A(2,3)和点B(m,2).由图象可知,对于同一个x,若y1>y2,则x的取值范围是 . 16.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论: A D F C B O E ①∠BOC=90º+∠A; ②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切; ③设OD=m,AE+AF=n,则S△AEF=mn; ④EF不能成为△ABC的中位线. 其中正确的结论是_____________. 三、专心解一解(本大题共8小题,满分72分) 17.(6分)先将代数式÷化简,再从-3<x<3的范围内选取一个合适的整数x代入求值. 18.(8分)某企业开发的一种罐装饮料,有大、小件两种包装,3大件4小件共装120缺罐,2大件3小件共装84罐.每大件与每小件各装多少罐? 19.(8分)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1. (1)证明:△A1AD1≌△CC1B; C B A D A1 C1 D1 (2)若∠ACB=30°,试问当点C1在线段AC上的什么位置时,四边形ABC1D1是菱形,并请说明理由. 20.(9分)在一次“爱心助学”捐款活动中,九(1)班同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图. (1)该班共有_____________名同学,学生捐款的众数是______________; (2)请你将图②的统计图补充完整; 图① 20元 20% 15元 32% 10元 5元 1 10 15 20 4 8 12 16 20 人数/人 捐款额/元 图② 6 16 10 (3)计算该班同学平均捐款多少元? A O B C E D 21.(9分)如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D作切线交BC于点E. (1)求证:DE=BC; (2)若tanC=,DE=2,求AD的长. 22.(10分) 问题背景: 在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积. 小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积. (1)请你将△ABC的面积直接填写在横线上.__________________ 思维拓展: (2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为a、2a、a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积. 探索创新: 图① 图② A C B (3)若△ABC三边的长分别为、、2(m>0,n>0,且m≠n),试运用构图法求出这三角形的面积. 23.(10分)某车站客流量大,旅客往往需长时间排队等候购票.经调查统计发现,每天开始售票时,约有300名旅客排队等候购票,同时有新的旅客不断进入售票厅排队等候购票,新增购票人数y(人)与售票时间x(分)的函数关系如图①所示;每个售票窗口票数y(人)与售票时间x(分)的函数关系如图②所示.某天售票厅排队等候购票的人数y(人)与售票时间x(分)的函数关系如图③所示,已知售票的前a分钟开放了两个售票窗口. (1)求a的值; (2)求售票到第60分钟时,售票厅排队等候购票的旅客人数; 1 4 3 1 240 300 78 a x/分 y/人 O O O 图① 图② 图③ x/分 y/人 x/分 y/人 (3)该车站在学习实践科学发展观的活动中,本着“以人为本,方便旅客”的宗旨,决定增设售票窗口.若要在开始售票后半小时内让所有排队购票的旅客都能购到票,以便后来到站的旅客能随到随购,请你帮助计算,至少需同时开放几个售票窗口? 24.(10分)如图,在平面直角坐标系中,O为坐标原点,边长为5的等边△OAB的OA边在x轴的正半轴上.点C、D同时从点O出发,点C以1个单位长/秒的速度向点A运动,点D以2个单位长/秒的速度沿折线OBA运动.设运动时间为t秒,0<t<5. (1)当0<t<时,证明:CD⊥OA; (2)若△OCD的面积为S,求S与t的函数关系式; (3)以点C为中心,将CD所在的直线顺时针旋转60°交AB于点E,若以点O、C、E、D为顶点的四边形是梯形,求点E的坐标. A A O O B B C D x x y y 备用图查看更多