北京市各区中考数学一模试题分类汇编新定义无答案新

北京市各区中考数学一模试题分类汇编新定义无答案新

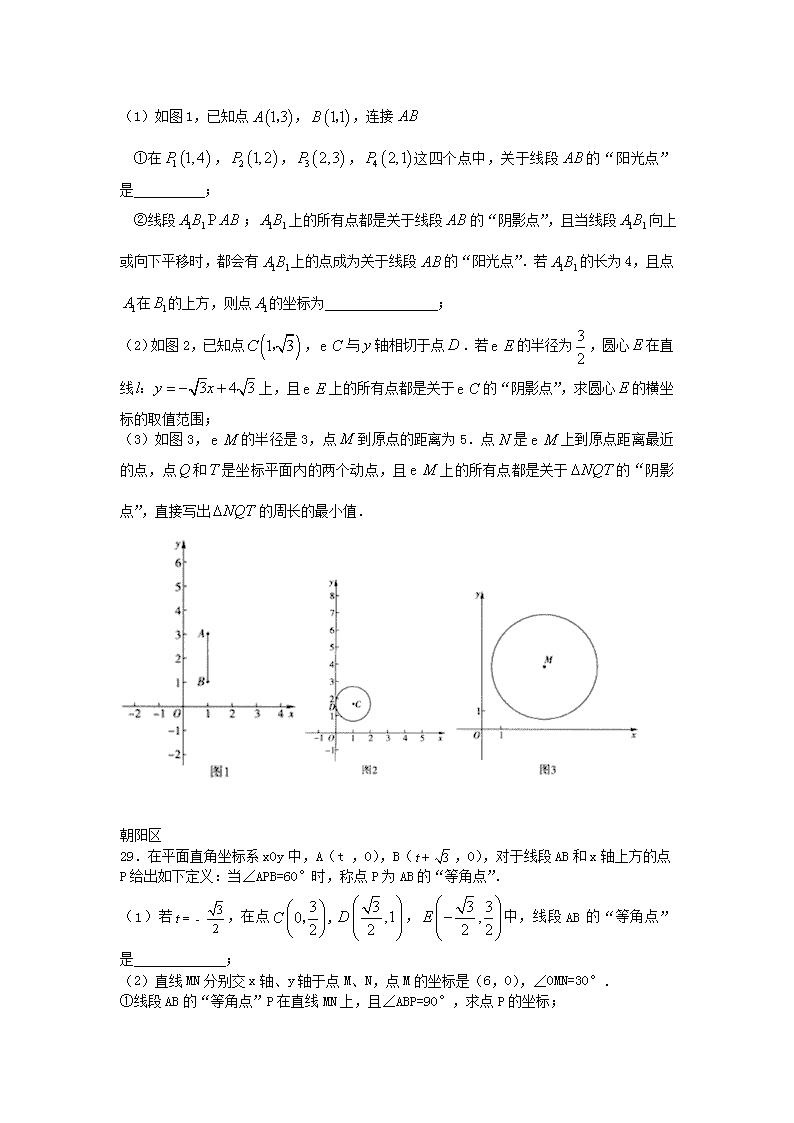
新定义 东城区 ‎29. 对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：若存在过点P的直线l交⊙C于异于点P的A，B两点，在P，A，B三点中，位于中间的点恰为以另外两点为端点的线段的中点时，则称点P为⊙C 的相邻点，直线l为⊙C关于点P的相邻线.‎ ‎（1）当⊙O的半径为1时，‎ ‎①分别判断在点D（，），E（0，-），F（4，0）中，是⊙O的相邻点有__________；‎ ‎②请从中的答案中，任选一个相邻点，在图1中做出⊙O关于它的一条相邻线，‎ 并说明你的作图过程.‎ ‎ ③点P在直线上，若点P为⊙O的相邻点，求点P横坐标的取值范围；‎ ‎（2）⊙C的圆心在x轴上，半径为1，直线与x轴，y轴分别交于点M，N，若线段MN上存在⊙C的相邻点P，直接写出圆心C的横坐标的取值范围．‎ ‎ ‎ 图1 备用图1‎ 备用图2‎ 西城区 ‎29．在平面直角坐标系中，对于点和图形,如果线段与图形无公共点，则称点为关于图形的“阳光点”；如果线段与图形有公共点，则称点为关于图形的“阴影点”．‎ ‎（1）如图1，已知点，，连接 ‎ ①在，，，这四个点中，关于线段的“阳光点”是 ；‎ ‎ ②线段；上的所有点都是关于线段的“阴影点”，且当线段向上或向下平移时，都会有上的点成为关于线段的“阳光点”．若的长为4，且点在的上方，则点的坐标为 ；‎ ‎（2）如图2，已知点，与轴相切于点．若的半径为，圆心在直线上，且上的所有点都是关于的“阴影点”，求圆心的横坐标的取值范围；‎ ‎（3）如图3，的半径是3，点到原点的距离为5．点是上到原点距离最近的点，点和是坐标平面内的两个动点，且上的所有点都是关于的“阴影点”，直接写出的周长的最小值．‎ 朝阳区 ‎29．在平面直角坐标系xOy中，A（t ，0），B（，0），对于线段AB和x轴上方的点P给出如下定义：当∠APB=60°时，称点P为AB的“等角点”．‎ ‎（1）若，在点,，中，线段AB的“等角点”是 ；‎ ‎（2）直线MN分别交x轴、y轴于点M、N，点M的坐标是（6，0），∠OMN=30°．‎ ‎①线段AB的“等角点”P在直线MN上，且∠ABP=90°，求点P的坐标；‎ ‎②在①的条件下，过点B作BQ⊥PA，交MN于点Q，求∠AQB的度数；‎ ‎③若线段AB的所有“等角点”都在△MON内部，则t的取值范围是 ．‎ 海淀区 ‎29．在平面直角坐标系中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的限距点的定义如下：若为直线PC与⊙C的一个交点，满足，则称 为点P关于⊙C的限距点，右图为点P及其关于⊙C的限距点的示意图． ‎ ‎（1） 当⊙O的半径为1时． ‎ ‎① 分别判断点M ，N ，T 关于⊙O的限距点是否存在？若存在，求其坐标； ‎ ‎②点D的坐标为（2,0），DE，DF分别切⊙O于点E，点F，点P在△DEF的边上.若点P关于⊙O的限距点存在，求点的横坐标的取值范围； ‎ ‎（2） 保持（1）中D，E，F三点不变，点P在△DEF的边上沿E→F→D→E的方向运动，⊙C的圆心C的坐标为（1,0），半径为r.请从下面两个问题中任选一个作答.‎ 温馨提示：答对问题1得2分，答对问题2得1分，两题均答不重复计分.‎ 问题1‎ 问题2‎ 若点P关于⊙C的限距点存在，且随点P的运动所形成的路径长为，则r的最小值为__________．‎ 若点P关于⊙C的限距点不存在，则r的取值范围为________.‎ 丰台区 ‎29. 如图，点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时，有-1 ≤ y1 - y2 ≤ 1成立，则称这两个函数在a ≤ x ≤ b上是“相邻函数”，否则称它们在a ≤ x ≤ b上是“非相邻函数”. 例如，点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点，当-3 ≤ x ≤ -1时，y1 - y2 = (3x + 1) - (2x - 1) = x + 2，通过构造函数y = x + 2并研究它在-3 ≤ x ≤ -1上的性质，得到该函数值的范围是-1 ≤ y ≤ 1，所以-1 ≤ y1 - y2 ≤ 1成立，因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.‎ ‎（1）判断函数y = 3x + 2与y = 2x + 1在－2 ≤ x≤ 0上是否为“相邻函数”，并说明理由；‎ ‎（2）若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”，求a的取值范围；‎ ‎（3）若函数y =与y =－2x + 4在1 ≤ x ≤ 2上是“相邻函数”，直接写出a的最大值与最小值.‎ 石景山区 ‎29．在平面直角坐标系中，图形在坐标轴上的投影长度定义如下：设点，是图形上的任意两点．若的最大值为，则图形在轴上的投影长度；若的最大值为，则图形在轴上的投影长度．如右图，图形在轴上的投影长度；在轴上的投影长度．‎ ‎（1）已知点，．如图1所示，若图形为△，则 ， ．‎ ‎（2）已知点，点在直线上，若图形为△．当时，求点的坐标．‎ ‎（3）若图形为函数的图象，其中．当该图形 满足时，请直接写出的取值范围．‎ 图1‎ 顺义区 ‎29．在平面直角坐标系xOy中，点P（a，b）的“变换点”Q的坐标定义如下；当，Q点坐标为（b，-a）；当a＜b时，Q点的坐标为（a，-b)．‎ ‎（1）求（-2，3），（6，-1）的变换点坐标；‎ ‎（2）已知直线l与x轴交于点A（4，0），与y轴交于点B（0，2）．若直线l上所有点的变换点组成一个新的图形，记作图形W．请画出图形W，并简要说明画图的思路；‎ ‎（3）若抛物线与图形W有三个交点，请直接写出c的取值范围．‎ 通州区 ‎29. 对于⊙P及一个矩形给出如下定义：如果⊙P上存在到此矩形四个顶点距离都相等的点，那么称⊙P是该矩形的“等距圆”．如图，在平面直角坐标系xOy中，矩形ABCD的顶点A的坐标为（，），顶点C、D在x轴上，且OC=OD.‎ ‎（1）当⊙P的半径为4时，‎ ‎①在P1（，），P2（，），P3（，）中可以成为矩形ABCD的“等距圆”的圆心的是_________________________；‎ ‎②如果点P在直线上，且⊙P是矩形ABCD的“等距圆”，求点P的坐标；‎ ‎（2）已知点P在轴上，且⊙P是矩形ABCD的“等距圆”，如果⊙P与直线AD没有公共点，直接写出点P的纵坐标m的取值范围.‎ 怀柔区 ‎29．给出如下规定：两个图形G1和G2，点P为G1上任一点，点Q为G2上任一点，如果线段PQ的长度存在最小值时，就称该最小值为两个图形G1和G2之间的“近距离”；如果线段PQ的长度存在最大值时，就称该最大值为两个图形G1和G2之间的“远距离” ．‎ 请你在学习，理解上述定义的基础上，解决下面问题：‎ 在平面直角坐标系xOy中，点A（-4， 3），B（-4，-3），C（4，-3），D（4， 3）．‎ ‎(1)请在平面直角坐标系中画出四边形ABCD，直接写出线段AB和线段CD的“近距离”和“远距离”．‎ ‎(2)设直线（b>0）与x轴，y轴分别交于点E，F，若线段EF与四边形ABCD的“近距离”是1，求它们的“远距离” ；‎ ‎(3)在平面直角坐标系xOy中，有一个矩形GHMN，若此矩形至少有一个顶点在以O为圆心，2为半径的圆上，其余各点可能在圆上或圆内.将四边形ABCD绕着点O旋转一周，在旋转的过程中，它与矩形GHMN的“远距离”的最大值是 ；“近距离”的最小值是 ．‎ 平谷区 ‎29．对于两个已知图形G1，G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G1，G2的“密距”，用字母d表示；当线段PQ的长度最大时，我们称这个最大的长度为图形G1，G2的“疏距”，用字母f表示．例如，当，时，点O与线段MN的“密距”为，点O与线段MN的“疏距”为．‎ ‎（1）已知，在平面直角坐标系xOy中，，，，，‎ ‎①点O与线段AB的“密距”为，“疏距”为；‎ ‎②线段AB与△COD的“密距”为，“疏距”为；‎ ‎（2）直线与x轴，y轴分别交于点E，F，以为圆心，1为半径作圆，当⊙C与线段EF的“密距”00）的图象上，且点D的坐标为（1，1），设点O，D，E的最佳外延正方形的边长为，请直接写出的取值范围. ‎ 门头沟区 ‎29．如图1，P为∠MON平分线OC上一点，以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点，如果∠APB在绕点P旋转时始终满足OA·OB=OP2，我们就把∠APB叫做∠MON的关联角．‎ 图1 图2 图3‎ ‎（1）如图2，P为∠MON平分线OC上一点，过P作PB⊥ON于B，AP⊥OC于P，那么∠APB ∠MON的关联角（填“是”或“不是”）．‎ ‎（2）① 如图3，如果∠MON=60°，OP=2，∠APB是∠MON的关联角，连接AB，求△AOB的面积和∠APB的度数；‎ ‎② 如果∠MON=α°（0°＜α°＜90°），OP=m，∠APB是∠MON的关联角，直接用含有α和m的代数式表示△AOB的面积．‎ ‎（3）如图4，点C是函数（x＞0）图象上一个动点，过点C的直线CD分别交x轴和y轴于A，B两点，且满足BC=2CA，直接写出∠AOB的关联角∠APB的顶点P的坐标．‎ ‎ ‎ 图4‎