- 2021-04-20 发布 |
- 37.5 KB |
- 9页


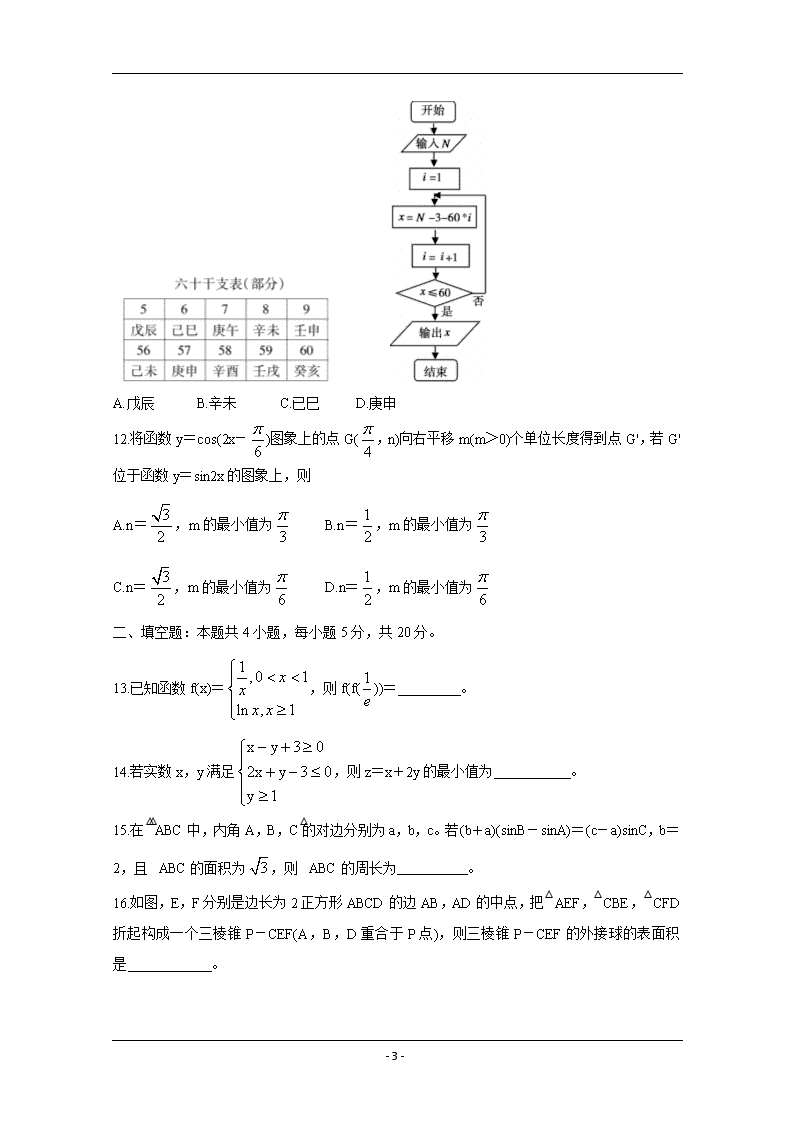
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
安徽省蚌埠市2021届高三上学期第一次质量监测(一模)试题 数学(文) Word版含答案
www.ks5u.com 蚌埠市2021届高三年级第一次教学质量监测 数学(文史类) 本试卷满分150分,考试时间120分钟 注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再涂选其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。 一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1.设集合U={0,1,2,3,4},A={0,1,2,3},B={1,2,4},则A∩(B)= A.{0} B.{0,3} C.{3} D.{1,3} 2.已知复数z=1-i,则|z2-1|= A. B.5 C. D.7 3.已知双曲线C:的离心率为2,则双曲线C的渐近线方程是 A.y=±x B.y=±x C.y=±x D.y=±2x 4.向量a为单位向量,向量a,b夹角为60°,a·b=1,则|b|= A. B.2 C. D. 5.函数f(x)=的图象大致为 6.已知θ∈(0,π),sin2θ=1-cos2θ,则tanθ= - 9 - A.-1 B.- C.1 D. 7.设0<b<a<1,则下列不等式中成立的是 A.ab<b2<1 B. C.1<2b<2a D.a2<ab<1 8.如图,网格纸上小正方形的边长为1,某多面体的三视图由图中粗线和虚线画出,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为 A.9+2 B.12 C.9+2 D.13 9.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人。第一组工人用第一种生产方式,第二组工人用第二种生产方式。根据工人完成生产任务的某项数据绘制了如下茎叶图: 根据茎叶图,得出第二种生产方式的效率更高。则茎叶图中的数据可能表示 A.单位时间生产的产品个数(单位:个) B.生产出的产品尺寸误差(单位:毫米) C.所获得的工资(单位:元) D.完成工作所用的工作时间(单位:分钟) 10.已知抛物线C:y2=4x的焦点为F,准线与x轴交于点E,过点E作圆(x-1)2+y2=1的切线,切点分别为A,B。则|AB|= A. B. C.2 D.3 11.干支是天干(甲、乙、…、癸)和地支(子、丑、…、亥)的合称,“干支纪年法”是我国传统的纪年法。如图是查找公历某年所对应干支的程序框图。例如公元2041年,即输入N=2041,执行该程序框图,运行相应的程序,输出x=58,从干支表中查出对应的干支为辛酉。我国古代杰出数学家秦九韶出生于公元1208年,则该年所对应的干支为 - 9 - A.戊辰 B.辛未 C.已巳 D.庚申 12.将函数y=cos(2x-)图象上的点G(,n)向右平移m(m>0)个单位长度得到点G',若G'位于函数y=sin2x的图象上,则 A.n=,m的最小值为 B.n=,m的最小值为 C.n=,m的最小值为 D.n=,m的最小值为 二、填空题:本题共4小题,每小题5分,共20分。 13.已知函数f(x)=,则f(f())= 。 14.若实数x,y满足,则z=x+2y的最小值为 。 15.在△ABC中,内角A,B,C的对边分别为a,b,c。若(b+a)(sinB-sinA)=(c-a)sinC,b=2,且△ABC的面积为,则△ABC的周长为 。 16.如图,E,F分别是边长为2正方形ABCD的边AB,AD的中点,把△AEF,△CBE,△CFD折起构成一个三棱锥P-CEF(A,B,D重合于P点),则三棱锥P-CEF的外接球的表面积是 。 - 9 - 三、解答题:共70分。解答应写出文字说明,证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答。 (一)必考题:共60分。 17.(12分) 已知等差数列{an}的首项a1=1,数列{}的前N项和为Sn,且S1+2,S2+2,S3+2成等比数列。 (1)求通项公式an; (2)求数列{}的前2n项和T2n。 18.(12分) 中国网络教育快速发展以来,中学生的学习方式发生了巨大转变。近年来,网络在线学习已成为重要的学习方式之一。为了解某学校上个月K,L两种网络学习方式的使用情况,从全校学生中随机抽取了100人进行调查,发现K,L两种学习方式都不使用的有15人,仅使用K和仅使用L的学生的学习时间分布情况如下: (1)求这100人中两种学习方式都使用的人数;若从这100人中随机抽取20人,求抽到仅使用一种学习方式的人数; (2)用这100人使用K,L两种学习方式的频率来代替概率,从全校学生中随机抽取1人,估计该学生上个月仅使用K,L两种学习方式中的一种,且使用时间不超过20小时的概率。 19.(12分) 如图,在棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠ABC=60°,AD=2,AB=AA1=4,F是AD的中点,且C1在底面上的投影E恰为CD的中点。 - 9 - (1)求证:AD⊥平面C1EF; (2)求四面体A1D1CE的体积。 20.(12分) 已知椭圆C:,F1,F2分别为椭圆的左、右焦点,过F2且与x轴不重合的直线l交C于P,Q两点,△PQF1的周长为8,△PF1F2面积的最大值为2。 (1)求C的方程; (2)点A(2,0),记直线PA,QA的斜率分别为k1,k2,求证:k1+k2=0。 21.(12分) 已知函数f(x)=x·(ax-tanx),x∈(),f(x)在x=处的切线斜率为-1。 (1)求a的值; (2)求函数f(x)的单调区间。 (二)选考题(共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号) 22.[选修4-4坐标系与参数方程](10分) 在极坐标系中,已知A(ρ1,)在直线l:ρ·sinθ=2上,点B(ρ2,)在圆C:ρ=4cosθ上(其中ρ≥0,θ∈[0,2π))。 (1)求|AB|; (2)求出直线l与圆C的公共点的极坐标。 23.[选修4-5不等式选讲](10分) 已知函数f(x)=|x-a2|+|x-a+1|。 (1)当a=1时,求不等式f(x)≥3的解集; (2)若f(x)≥3,求实数a的取值范围。 - 9 - - 9 - - 9 - - 9 - - 9 -查看更多