高考必做的百例导数压轴题(共100页)
◇导数专题
目 录
一、导数单调性、极值、最值的直接应用 (1)
二、交点与根的分布 (23)
三、不等式证明 (31)
(一)作差证明不等式
(二)变形构造函数证明不等式
(三)替换构造不等式证明不等式
四、不等式恒成立求字母范围 (51)
(一)恒成立之最值的直接应用
(二)恒成立之分离常数
(三)恒成立之讨论字母范围
五、函数与导数性质的综合运用 (70)
六、导数应用题 (84)
七、导数结合三角函数 (85)
书中常用结论
⑴,变形即为,其几何意义为上的的点与原点连线斜率小于1.
⑵
⑶
⑷.
一、导数单调性、极值、最值的直接应用
1. (切线)设函数.
(1)当时,求函数在区间上的最小值;
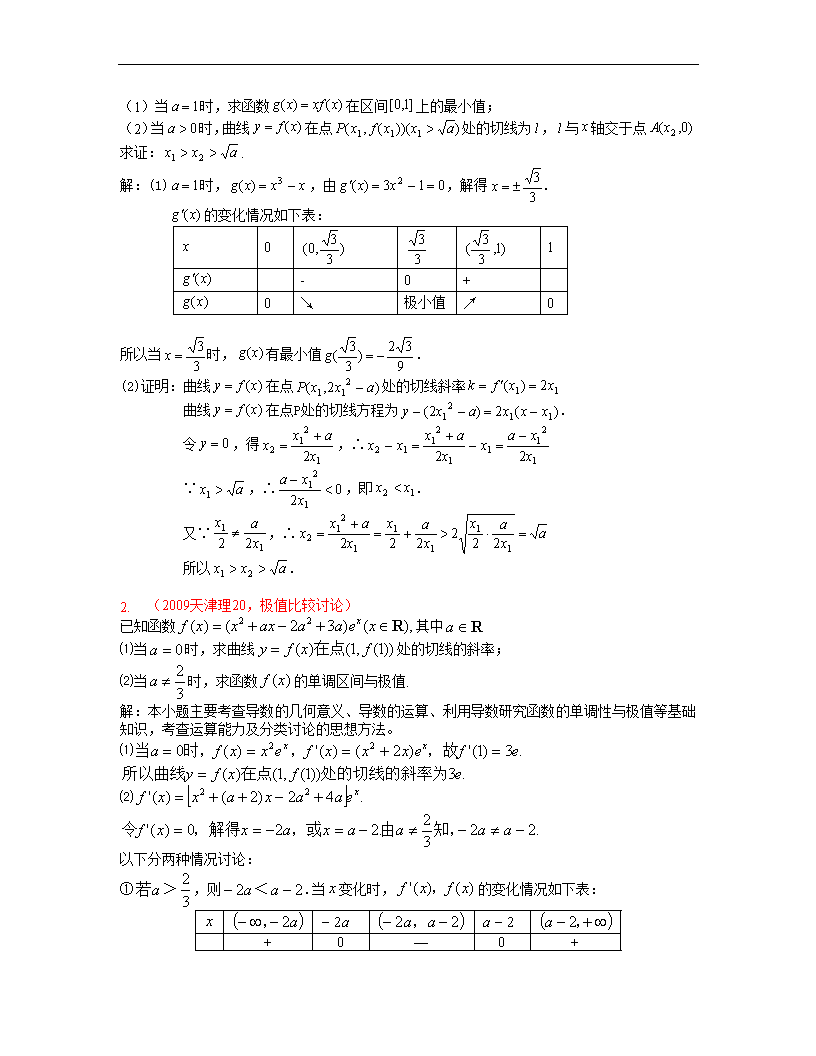
(2)当时,曲线在点处的切线为,与轴交于点求证:.
解:(1)时,,由,解得.
的变化情况如下表:
0
1
-
0
+
0
↘
极小值
↗
0
所以当时,有最小值.
(2)证明:曲线在点处的切线斜率
曲线在点P处的切线方程为.
令,得,∴
∵,∴,即.
又∵,∴
所以.
2. (2009天津理20,极值比较讨论)
已知函数其中
⑴当时,求曲线处的切线的斜率;w.w.w.k.s.5.u.c.o.m
⑵当时,求函数的单调区间与极值.
解:本小题主要考查导数的几何意义、导数的运算、利用导数研究函数的单调性与极值等基础知识,考查运算能力及分类讨论的思想方法。
⑴
⑵ w.w.w.k.s.5.u.c.o.m
以下分两种情况讨论:
①>,则<.当变化时,的变化情况如下表:
+
0
—
0
+
↗
极大值
↘
极小值
↗
w.w.w.k.s.5.u.c.o.m
②<,则>,当变化时,的变化情况如下表:
+
0
—
0
+
↗
极大值
↘
极小值
↗
w.w.w.k.s.5.u.c.o.m
1. 已知函数
⑴设两曲线有公共点,且在公共点处的切线相同,若,试建立 关于的函数关系式,并求的最大值;
⑵若在(0,4)上为单调函数,求的取值范围。
1. (最值,按区间端点讨论)
已知函数f(x)=lnx-.
(1)当a>0时,判断f(x)在定义域上的单调性;
(2)若f(x)在[1,e]上的最小值为,求a的值.
解:(1)由题得f(x)的定义域为(0,+∞),且 f ′(x)=+=.
∵a>0,∴f ′(x)>0,故f(x)在(0,+∞)上是单调递增函数.
(2)由(1)可知:f ′(x)=,
①若a≥-1,则x+a≥0,即f ′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,
∴f(x)min=f(1)=-a=,∴a=- (舍去).
②若a≤-e,则x+a≤0,即f ′(x)≤0在[1,e]上恒成立,此时f(x)在[1,e]上为减函数,
∴f(x)min=f(e)=1-=,∴a=-(舍去).
③若-e
0,∴f(x)在(-a,e)上为增函数,
∴f(x)min=f(-a)=ln(-a)+1=⇒a=-.
综上可知:a=-.
2. (最值直接应用)已知函数,其中.
(Ⅰ)若是的极值点,求的值;
(Ⅱ)求的单调区间;
(Ⅲ)若在上的最大值是,求的取值范围.
解:(Ⅰ).
依题意,令,解得 . 经检验,时,符合题意.
(Ⅱ)解:① 当时,.
故的单调增区间是;单调减区间是.
② 当时,令,得,或.
当时,与的情况如下:
↘
↗
↘
所以,的单调增区间是;单调减区间是和.
当时,的单调减区间是.
当时,,与的情况如下:
↘
↗
↘
所以,的单调增区间是;单调减区间是和.
③ 当时,的单调增区间是;单调减区间是.
综上,当时,的增区间是,减区间是;
当时,的增区间是,减区间是和;
当时,的减区间是;
当时,的增区间是;减区间是和.
(Ⅲ)由(Ⅱ)知 时,在上单调递增,由,知不合题意.
当时,在的最大值是,
由,知不合题意.
当时,在单调递减,
可得在上的最大值是,符合题意.
所以,在上的最大值是时,的取值范围是.
1. (2010北京理数18)
已知函数=ln(1+)-+(≥0).
(Ⅰ)当=2时,求曲线=在点(1,(1))处的切线方程;
(Ⅱ)求的单调区间.
解:(I)当时,,
由于,,
所以曲线在点处的切线方程为
即
(II),.
当时,.
所以,在区间上,;在区间上,.
故得单调递增区间是,单调递减区间是.
当时,由,得,
所以,在区间和上,;在区间上,
故得单调递增区间是和,单调递减区间是.
当时, 故得单调递增区间是.
当时,,得,.
所以没在区间和上,;在区间上,
故得单调递增区间是和,单调递减区间是
1. (2010山东文21,单调性)
已知函数
⑴当时,求曲线在点处的切线方程;
⑵当时,讨论的单调性.
解:⑴
⑵因为 ,
所以 ,,
令
1. (是一道设计巧妙的好题,同时用到e底指、对数,需要构造函数,证存在且唯一时结合零点存在性定理不好想,⑴⑵联系紧密)
已知函数
⑴若函数φ (x) = f (x)-,求函数φ (x)的单调区间;
⑵设直线l为函数f (x)的图象上一点A(x0,f (x0))处的切线,证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
解:(Ⅰ) ,.
∵且,∴∴函数的单调递增区间为.
(Ⅱ)∵ ,∴,
∴ 切线的方程为, 即, ①
设直线与曲线相切于点,
∵,∴,∴,∴.
∴直线也为, 即, ②
由①②得 ,∴.
下证:在区间(1,+)上存在且唯一.
由(Ⅰ)可知,在区间上递增.
又,,
结合零点存在性定理,说明方程必在区间上有唯一的根,这个根就是所求的唯一,故结论成立.
1. (最值应用,转换变量)
设函数.
(1)讨论函数在定义域内的单调性;
(2)当时,任意,恒成立,求实数的取值范围.
解:⑴.
当时,,增区间为,减区间为,.
当时,,减区间为.
当时,,增区间为,减区间为,.
⑵由⑴知,当时,在上单调递减,
∴,≤,
即≤.
∵恒成立,
∴>,即,
又,∴.
∵,∴,∴≤.
2. (最值应用)
已知二次函数对都满足且,设函数(,).
(Ⅰ)求的表达式;
(Ⅱ)若,使成立,求实数的取值范围;
(Ⅲ)设,,求证:对于,恒有.
解:(Ⅰ)设,于是
所以
又,则.所以. …………3分
(Ⅱ)
当m>0时,由对数函数性质,f(x)的值域为R;…………4分
当m=0时,对,恒成立; …………5分
当m<0时,由,列表:
x
-
0
+
减
极小
增
所以若,恒成立,则实数m的取值范围是.
故使成立,实数m的取值范围.…………9分
(Ⅲ)因为对,所以在内单调递减.
于是
记,则
所以函数在是单调增函数,
所以,故命题成立. …………12分
1. 设是函数的一个极值点.
(1)求与的关系式(用表示),并求的单调区间;
(2)设,若存在,使得 成立,求的取值范围.
解:(1)∵
∴ 由题意得:,即,
∴且
令得,
∵是函数的一个极值点
∴,即
故与的关系式为.
当时,,由得单增区间为:;
由得单减区间为:和;
当时,,由得单增区间为:;
由得单减区间为:和;
(2)由(1)知:当时,,在上单调递增,在上单调递减,,
∴在上的值域为.
易知在上是增函数,
∴在上的值域为.
由于,
又∵要存在,使得成立,
∴必须且只须解得:.
所以,的取值范围为.
1. .
(1)若,求函数的极值;
(2)若是函数的一个极值点,试求出关于的关系式(用表示),并确定的单调区间;
(3)在(2)的条件下,设,函数.若存在使得
成立,求的取值范围.
解:(1)∵
当时,,则.
令得,∵,∴,解得
∵当时,,
当时,当时
∴当时,函数有极大值,,
当时,函数有极小值,.
(2)由(1)知
∵是函数的一个极值点 ∴
即,解得
则=
令,得或
∵是极值点,∴,即 .
当即时,由得或
由得
当即时,由得或
由得.
综上可知:
当时,单调递增区间为和,递减区间为
当时,单调递增区间为和,递减区间为。
(3)由2)知:当a>0时,在区间(0,1)上的单调递减,
在区间(1,4)上单调递增,
∴函数在区间上的最小值为
又∵,,
∴函数在区间[0,4]上的值域是,即]
又在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是.
∵-==,
∴存在使得成立只须
-<1..
1. (2010山东,两边分求,最小值与最大值)
已知函数.
⑴当时,讨论的单调性;
⑵设当时,若对任意,存在,使,求实数取值范围.
解:本题将导数、二次函数、不等式知识有机的结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力.
(1)直接利用函数与导数的关系讨论函数的单调性;(2)利用导数求出的最小值、利用二次函数知识或分离常数法求出在闭区间[1,2]上的最大值,然后解不等式求参数.
⑴,
令
①当时,,当,函数单调递减;当,函数单调递增.
②当时,由,即,解得.
当时,恒成立,此时,函数单调递减;
当时,,时,函数单调递减;
时,,函数单调递增;
时,,函数单调递减.
当时,当,函数单调递减;
当,函数单调递增.
综上所述:当时,函数在单调递减,单调递增;
当时,恒成立,此时,函数在单调递减;
当时,函数在递减,递增,递减.
⑵当时,在(0,1)上是减函数,在(1,2)上是增函数,所以对任意,
有,
又已知存在,使,所以,,(※)
又
当时,与(※)矛盾;
当时,也与(※)矛盾;
当时,.
综上,实数的取值范围是.
1. 设函数.
(Ⅰ)当时,过原点的直线与函数的图象相切于点P,求点P的坐标;
(Ⅱ)当时,求函数的单调区间;
(Ⅲ)当时,设函数,若对于],[0,1]
使≥成立,求实数b的取值范围.(是自然对数的底,)
解:函数的定义域为,
(Ⅰ)设点,当时,,则,,∴
解得,故点P 的坐标为
(Ⅱ)
∵ ∴
∴当,或时,当时,
故当时,函数的单调递增区间为;
单调递减区间为,
(Ⅲ)当时,由(Ⅱ)可知函数在上是减函数,在上为增函数,在上为减函数,且,
∵,又,∴,
∴,故函数在上的最小值为
若对于,使 ≥成立在上的最小值不大于
在上的最小值(*)
又,
①当时,在上为增函数,与(*)矛盾
②当时,,
由及得,
③当时,在上为减函数,
,此时 综上,的取值范围是
1. (2010山东,两边分求,最小值与最大值)
已知函数.
⑴求在上的最小值;
⑵若存在(是常数,=2.71828)使不等式成立,求实数的取值范围;
⑶证明对一切都有成立.
解:⑴,
⑵由题意知
,
而,故
(Ⅲ) 等价证明
由⑴知
.
1. (最值应用)
设函数,且,其中是自然对数的底数.
⑴求与的关系;
⑵若在其定义域内为单调函数,求的取值范围;
⑶设,若在上至少存在一点,使得>成立,求实数的取值范围.
解:(1)由题意得
而,所以、的关系为.
(2)由(1)知,
.令,
要使在其定义域内单调,只需恒成立.
①当时,,因为>,所以<0,<0,
∴在内是单调递减函数,即适合题意;
②当>0时,,∴,
只需,即,
∴在内为单调递增函数,故适合题意.
③当<0时,,其图像为开口向下的抛物线,对称轴为,只要,即时,在恒成立,故<0适合题意.
综上所述,的取值范围为.
(3)∵在上是减函数,
∴时,;时,,即,
①当时,由(2)知在上递减<2,不合题意;
②当0<<1时,由,
又由(2)知当时,在上是增函数,
∴<,不合题意;
③当时,由(2)知在上是增函数,<2,又在上是减函数,故只需>,,而,, 即 >2,解得> ,
综上,的取值范围是.
1. (2011湖南文,第2问难,单调性与极值,好题)
设函数
⑴讨论函数的单调性;
⑵若有两个极值点,记过点的直线斜率为,问:是否存在,使得?若存在,求出的值;若不存在,请说明理由.
解:⑴的定义域为
令
①当故上单调递增.
②当的两根都小于0,在上,,故上单调递增.
③当的两根为,
当时, ;当时,;当时,,故分别在上单调递增,在上单调递减.
⑵由⑴知,若有两个极值点,则只能是情况③,故.
因为,
所以
又由⑴知,,于是
若存在,使得则.即.
亦即
再由⑴知,函数在上单调递增,而,所以这与式矛盾.故不存在,使得
1. (构造函数,好,较难)
已知函数.
⑴求函数的单调增区间;
⑵记函数的图象为曲线,设点是曲线上两个不同点,如果曲线上存在点,使得:①;②曲线在点处的切线平行于直线,则称函数存在“中值相依切线”.试问:函数是否存在中值相依切线,请说明理由.
解:(Ⅰ)函数的定义域是.
由已知得,.
ⅰ 当时, 令,解得;函数在上单调递增
ⅱ 当时,
①当时,即时, 令,解得或;
函数在和上单调递增
②当时,即时, 显然,函数在上单调递增;
③当时,即时, 令,解得或
函数在和上单调递增.
综上所述:
⑴当时,函数在上单调递增
⑵当时,函数在和上单调递增
⑶当时,函数在上单调递增;
⑷当时,函数在和上单调递增.
(Ⅱ)假设函数存在“中值相依切线”.
设,是曲线上的不同两点,且,
则,.
.
曲线在点处的切线斜率,
依题意得:.
化简可得 , 即=.
设 (),上式化为:,
,令,.
因为,显然,所以在上递增,显然有恒成立.
所以在内不存在,使得成立.
综上所述,假设不成立.所以,函数不存在“中值相依切线”
1. (2011天津理19,综合应用)
已知,函数,.(的图象连续)
⑴求的单调区间;
⑵若存在属于区间的,且,使,证明:.
解:⑴,.令,则.
当变化时,,的变化情况如下表:
单调递增
极大值
单调递减
所以的单调增区间是,单调减区间是.
⑵由及的单调性知.从而在区间上的最小值为.
又由,,则.
所以即
所以.
1. (恒成立,直接利用最值)
已知函数,
⑴若是函数的一个极值点,求;
⑵讨论函数的单调区间;
⑶若对于任意的,不等式在上恒成立,求的取值范围.
解:⑴,
因为是函数的一个极值点,所以,得.
又,所以.
⑵因为的定义域是,
.
①当时,列表
+
-
+
增
减
增
在,是增函数;在是减函数.
②当时,,在是增函数.
③当时,列表
+
-
+
增
减
增
在,是增函数;在是减函数.
⑶
1. (最值与图象特征应用)
设,函数为自然对数的底数).
⑴判断的单调性;
⑵若上恒成立,求a的取值范围.
解:⑴∵
令
①当在R上为减函数.
②当
在R上为减函数.
③当时,由得
由得
上为增函数;
上为减函数.
⑵由⑴知
①当上为减函数.
②当
在[1,2]上不恒成立,∴a的取值范围是
2. (单调性)
已知=ln(x+2)-x2+bx+c
⑴若函数在点(1,y)处的切线与直线3x+7y+2=0垂直,且f(-1)=0,求函数在区间[0,3]上的最小值;
⑵若在区间[0,m]上单调,求b的取值范围.
解:⑴,依题意令= ,=0,解得b=4,c=5.
x
0
(0,)
(,3)
3
y′
+
0
-
y
ln2+5
极大
8+ln5
因为8+ln5>5+ln2 ∴x=0时在[0,3]上最小值=5+ln2.
⑵若在区间[0,m]上单调,有两种可能
①令≥0得b≥2x-,在[0,m]上恒成立
而y=2x-在[0,m]上单调递增,最大值为2m-,∴b≥2m-.
②令≤0 得b≤2x-,
而 y=2x-在[0,m]单增,最小为y=-,∴b≤-.
故b≥2m-或b≤-时在[0,m]上单调.
1. (单调性,用到二阶导数的技巧)
已知函数
⑴若,求的极大值;
⑵若在定义域内单调递减,求满足此条件的实数k的取值范围.
解:⑴定义域为
令 由
由
即上单调递增,在上单调递减
时,F(x)取得极大值
⑵的定义域为(0,+∞),
由G (x)在定义域内单调递减知:在(0,+∞)内恒成立
令,则 由
∵当时为增函数
当时,为减函数
∴当x = e时,H(x)取最大值
故只需恒成立,
又当时,只有一点x = e使得不影响其单调性
二、交点与根的分布
1. (2008四川22,交点个数与根的分布)
已知是函数的一个极值点.
⑴求;
⑵求函数的单调区间;
⑶若直线与函数的图像有个交点,求的取值范围.
解:⑴,
是函数的一个极值点.
,
⑵由⑴,
令,得,,和随的变化情况如下:
1
3
0
0
增
极大值
减
极小值
增
的增区间是,;减区间是(1,3).
⑶由②知,在上单调递增,在上单调递增,在上单调递减.
∴,.
又时,;时,;
可据此画出函数的草图(图略),由图可知,
当直线与函数的图像有3个交点时,的取值范围为.
2. 已知函数在上是减函数,在上是增函数,函数在
上有三个零点.
(1)求的值;
(2)若1是其中一个零点,求的取值范围;
(3)若,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
⑶=2x+lnx,设过点(2,5)与曲线g (x)的切线的切点坐标为
∴,即
∴,令h(x)=,∴==0,∴
∴h(x)在(0,2)上单调递减,在(2,)上单调递增
又,h(2)=ln2-1<0,
∴h(x)与x轴有两个交点,∴过点(2,5)可作2条曲线y=g(x)的切线.
1. (交点个数与根的分布)
已知函数
⑴求在区间上的最大值
⑵是否存在实数使得的图像与
的图像有且只有三个不同的交点?若存在,求出的取值范围;若不存在,说明理由。
解:⑴
当即时,在上单调递增,
当即时,
当时,在上单调递减,
综上
⑵函数的图像与的图像有且只有三个不同的交点,即函数
的图像与轴的正半轴有且只有三个不同的交点。
当时,是增函数;
当时,是减函数;
当时,是增函数;
当或时,
当充分接近0时,当充分大时,
要使的图像与轴正半轴有三个不同的交点,必须且只须
即
∴存在实数,使得函数与的图像有且只有三个不同的交点,的取值范围为
1. (交点个数与根的分布)
已知函数
⑴求f(x)在[0,1]上的极值;
⑵若对任意成立,求实数a的取值范围;
⑶若关于x的方程在[0,1]上恰有两个不同的实根,求实数b的取值范围.
解:⑴,
令(舍去)
单调递增;当递减.
上的极大值.
⑵由得
设,,
依题意知上恒成立,
,
,
上单增,要使不等式①成立,
当且仅当
⑶由
令,
当上递增;
上递减,
而,
恰有两个不同实根等价于
1. (2009宁夏,利用根的分布)
已知函数
⑴如,求的单调区间;
⑵若在单调增加,在单调减少,证明:<6. w.w.w.k.s.5.u.c.o.m
解:⑴时,,故w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
当当
从而单调减少.
⑵
由条件得
从而
因为
所以
将右边展开,与左边比较系数得,故
又由此可得于是 w.w
2. (2009天津文,利用根的分布讨论)
设函数,其中
⑴当时,求曲线在点处的切线的斜率
⑵求函数的单调区间与极值
⑶已知函数有三个互不相同的零点,且,若对任意的恒成立,求的取值范围.
解:⑴当
所以曲线在点处的切线斜率为1.
⑵,令,得到
因为,
当x变化时,的变化情况如下表:
+
0
-
0
+
↓
极小值
↑
极大值
↓
在和内减函数,在内增函数。
函数在处取得极大值,且=
函数在处取得极小值,且=
⑶由题设
所以方程=0由两个相异的实根,故,且,解得
因为(难点)
若,而,不合题意;
若则对任意的有
则,又,所以函数在的最小值为0,于是对任意的,恒成立的充要条件是,解得,综上,m的取值范围是
1. (2007全国II理22,转换变量后为根的分布)
已知函数.
(1)求曲线在点处的切线方程;
(2)设,如果过点可作曲线的三条切线,证明:.
解:(1).在点处的切线方程为,
即.
(2)如果有一条切线过点,则存在,使.
若过点可作曲线的三条切线,
则方程 有三个相异的实数根.
记 ,则.
当变化时,变化情况如下表:
0
0
0
极大值
极小值
如果过可作曲线三条切线,
即有三个相异的实数根,则即 .
1. 已知函数在点处的切线方程为.
⑴求函数的解析式;
⑵若对于区间上任意两个自变量的值都有,求实数的最小值;
⑶若过点可作曲线的三条切线,求实数的取值范围.
解:⑴.…………………………………………………………2分
根据题意,得即解得……………………3分
所以.………………………………………………………………4分
⑵令,即.得.
1
2
+
+
增
极大值
减
极小值
增
2
因为,,
所以当时,,.………………………………6分
则对于区间上任意两个自变量的值,都有
,所以.
所以的最小值为4.……………………………………………………………………8分
⑶因为点不在曲线上,所以可设切点为.
则.
因为,所以切线的斜率为.………………………………9分
则=,………………………………………………………………11分
即.
因为过点可作曲线的三条切线,
所以方程有三个不同的实数解.
所以函数有三个不同的零点.
则.令,则或.
0
2
+
+
增
极大值
减
极小值
增
则 ,即,解得.
1. (2011省模,利用⑴的结论,转化成根的分布分题)
已知,函数(其中)
(I)求函数在区间上的最小值;
(II)是否存在实数,使曲线在点处的切线与y轴垂直?若存在,求出的值;若不存在,请说明理由。
1. 已知函数,函数是区间[-1,1]上的减函数.
(I)求的最大值;
(II)若上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程的根的个数.
解:(I),上单调递减,
在[-1,1]上恒成立,,故的最大值为
(II)由题意
(其中),恒成立,令,
则,恒成立,
(Ⅲ)由
令
当[来源上为增函数;
当时,为减函数;
当[来源:学*科*网]
而方程无解;
当时,方程有一个根;
当时,方程有两个根.
三、不等式证明
作差证明不等式
2. (2010湖南,最值、作差构造函数)
已知函数.
(1)求函数的单调递减区间;
(2)若,求证:≤≤x.
解:(1)函数f (x)的定义域为(-1,+∞),,
由 得:,∴x>0,∴f (x)的单调递减区间为(0,+∞).
(2)证明:由(1)得x∈(-1,0)时,,
当x∈(0,+∞)时,,且
∴x>-1时,f (x)≤f (0),∴≤0,≤x
令,则,
∴-1<x<0时,,x>0时,,且
∴x>-1时,g (x)≥g (0),即≥0
∴≥,∴x>-1时,≤≤x.
1. (2007湖北20,转换变量,作差构造函数,较容易)
已知定义在正实数集上的函数,,其中.设两曲线,有公共点,且在该点处的切线相同.
⑴用表示,并求的最大值;
⑵求证:当时,.
解:⑴设与在公共点处的切线相同.
,,由题意,.
即由得:,或(舍去).
即有.
令,则.于是
当,即时,;
当,即时,.
故在为增函数,在为减函数,
于是在的最大值为.
⑵设,
则.
故在为减函数,在为增函数,
于是函数在上的最小值是.
故当时,有,即当时,.
1. (2009全国II理21,字母替换,构造函数)
设函数有两个极值点,且
⑴求的取值范围,并讨论的单调性;
⑵证明:.
解: ⑴
令,其对称轴为。
由题意知是方程的两个均大于的不相等的实根,
其充要条件为,得
当时,在内为增函数;
当时,在内为减函数;
当时,在内为增函数;
⑵由⑴知,
由得,
设,
则
当时,在单调递增;
当时,,在单调递减。
所以,
故.
变形构造函数证明不等式
1. (变形构造新函数,一次)
已知函数.
⑴试讨论在定义域内的单调性;
⑵当<-1时,证明:,.求实数的取值范围.
解:⑴函数的定义域为,.
当时,增区间为,减区间为;
当≤≤0时,增区间为;
当时,增区间为,减区间为.
⑵当>0时,在区间(0,1)上单调递增,
不妨设,则,
∴等价于,即.
构造,则>0.
∴在上是增函数,当时,,
即,即.
又当>0时,在区间(0,1)上单调递增,
∴.
∴,即.
2. (2011辽宁理21,变形构造函数,二次)
已知函数.
⑴讨论函数的单调性;
⑵设,如果对任意,≥,求的取值范围.
解:⑴的定义域为(0,+∞). .
当时,>0,故在(0,+∞)单调增加;
当时,<0,故在(0,+∞)单调减少;
当-1<<0时,令=0,解得.
则当时,>0;时,<0.
故在单调增加,在单调减少.
⑵不妨假设,而<-1,由⑴知在(0,+∞)单调减少,从而
,
等价于,…… ①
令,则
①等价于在(0,+∞)单调减少,即.
从而,设并设,
∴,∴≤
故a的取值范围为(-∞,-2].
1. (2010辽宁文21,构造变形,二次)
已知函数.
⑴讨论函数的单调性; K^S*5U.C#
⑵设,证明:对任意,.
解:⑴ f(x)的定义域为(0,+),.
当a≥0时,>0,故f(x)在(0,+)单调增加;
当a≤-1时,<0, 故f(x)在(0,+)单调减少;
当-1<a<0时,令=0,解得x=.当x∈(0, )时, >0;
x∈(,+)时,<0,
故f(x)在(0, )单调增加,在(,+)单调减少.
⑵不妨假设x1≥x2.由于a≤-2,故f(x)在(0,+)单调减少.
所以等价于≥4x1-4x2,
即f(x2)+ 4x2≥f(x1)+ 4x1.
令g(x)=f(x)+4x,则+4=.
设,≤-1,对称轴为,
结合图象知≤≤0,
于是≤=≤0.
从而g(x)在(0,+)单调减少,故g(x1) ≤g(x2),
即 f(x1)+ 4x1≤f(x2)+ 4x2,故对任意x1,x2∈(0,+) ,
1. (辽宁,变形构造,二次)
已知函数f(x)=x2-ax+(a-1),.
(1)讨论函数的单调性;w.w.w.k.s.5.u.c.o.m
(2)证明:若,则对任意x,x,xx,有.
解:(1)的定义域为.
①若即,则,故在单调增加。
②若,而,故,则当时,;
当及时,
故在单调减少,在单调增加。
③若,即,同理在单调减少,在单调增加.
⑵考虑函数
则(另一种处理)
由于10,上存在极值,求实数a的取值范围;
(Ⅱ)如果当时,不等式恒成立,求实数k的取值范围;
解:(Ⅰ)因为, x >0,则,
当时,;当时,.
所以在(0,1)上单调递增;在上单调递减,
所以函数在处取得极大值.
因为函数在区间(其中)上存在极值,
所以 解得.
(Ⅱ)不等式即为 记
所以
令,则,
, 在上单调递增,
,从而,
故在上也单调递增, 所以,所以 .
1. (2010湖南,分离常数,构造函数)
已知函数 对任意的恒有.
⑴证明:当
⑵若对满足题设条件的任意b、c,不等式恒成立,求M的最小值。
1. (第3问不常见,有特点,由特殊到一般,先猜后证)已知函数
(Ⅰ)求函数f (x)的定义域
(Ⅱ)确定函数f (x)在定义域上的单调性,并证明你的结论.
(Ⅲ)若x>0时恒成立,求正整数k的最大值.
解:(1)定义域
(2)单调递减。
当,令,
故在(-1,0)上是减函数,即,
故此时
在(-1,0)和(0,+)上都是减函数
(3)当x>0时,恒成立,令
又k为正整数,∴k的最大值不大于3
下面证明当k=3时,恒成立
当x>0时 恒成立
令,则
,,当
∴当取得最小值
当x>0时, 恒成立,因此正整数k的最大值为3
2. (恒成立,分离常数,涉及整数、较难的处理)
已知函数
(Ⅰ)试判断函数上单调性并证明你的结论;
(Ⅱ)若恒成立,求整数k的最大值;(较难的处理)
(Ⅲ)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n-3.
解:(I)
上递减.
(II)
则上单调递增,
又
存在唯一实根a,且满足
当
∴
故正整数k的最大值是3 .
(Ⅲ)由(Ⅱ)知
∴
令,则
∴ln(1+1×2)+ln(1+2×3)+…+ln[1+n(n+1)]
∴(1+1×2)(1+2×3)…[1+n(n+1)]>e2n-3
1. (分离常数,双参,较难)已知函数,.
(1)若函数依次在处取到极值.
①求的取值范围;②若,求的值.
(2)若存在实数,使对任意的,不等式 恒成立.求正整数的最大值.
解:(1)①
②
.
(2)不等式 ,即,即.
转化为存在实数,使对任意,不等式恒成立,即不等式在上恒成立。
即不等式在上恒成立。
设,则。
设,则,因为,有。
故在区间上是减函数。
又
故存在,使得。
当时,有,当时,有。
从而在区间上递增,在区间上递减。
又
所以当时,恒有;当时,恒有;
故使命题成立的正整数的最大值为5.
1. (2008湖南理22,分离常数,复合的超范围)
已知函数
⑴求函数的单调区间;
⑵若不等式对任意的都成立(其中e是自然对数的底数),求a的最大值.(分离常数)
解: ⑴函数的定义域是,
设则
令则
当时, 在(-1,0)上为增函数,
当x>0时,在上为减函数.
所以h(x)在x=0处取得极大值,而h(0)=0,所以,
函数g(x)在上为减函数.
于是当时,当x>0时,
所以,当时,在(-1,0)上为增函数.
当x>0时,在上为减函数.
故函数的单调递增区间为(-1,0),单调递减区间为.
⑵不等式等价于不等式
由知,>0,∴上式变形得
设,则则
由⑴结论知,(≤)即
所以于是G(x)在上为减函数.
故函数在上的最小值为
所以a的最大值为
1. (变形,分离常数)
已知函数(a为实常数).
(1)若,求证:函数在(1,+∞)上是增函数;
(2)求函数在[1,e]上的最小值及相应的值;
(3)若存在,使得成立,求实数a的取值范围.
解:⑴当时,,当,,
故函数在上是增函数.
⑵,当,.
若,在上非负(仅当,x=1时,),故函数在上是增函数,此时.
若,当时,;当时,,此时
是减函数;当时,,此时是增函数.
故.
若,在上非正(仅当,x=e时,),故函数 在
上是减函数,此时.
⑶不等式,可化为.
∵, ∴且等号不能同时取,所以,即,
因而()
令(),又,
当时,,,
从而(仅当x=1时取等号),所以在上为增函数,
故的最小值为,所以a的取值范围是.
1. (分离常数,转换变量,有技巧)
设函数.
⑴若函数在处与直线相切:
①求实数的值;②求函数在上的最大值;
⑵当时,若不等式≥对所有的都成立,求实数的取值范围.
解:(1)①。
∵函数在处与直线相切解得 .
②
当时,令得;令,得,上单调递增,在[1,e]上单调递减,.
(2)当b=0时,若不等式对所有的都成立,则对所有的都成立,
即对所有的都成立,
令为一次函数, .
上单调递增,,
对所有的都成立.
..
(注:也可令所有的都成立,分类讨论得对所有的都成立,,请根据过程酌情给分)
恒成立之讨论字母范围
1. (2007全国I,利用均值,不常见)
设函数.
⑴证明:的导数;
⑵若对所有都有,求的取值范围.
解:⑴的导数.由于,故.
(当且仅当时,等号成立).
⑵令,则,
①若,当时,,
故在上为增函数,
所以,时,,即.
②若,方程的正根为,
此时,若,则,故在该区间为减函数.
所以,时,,即,与题设相矛盾.
综上,满足条件的的取值范围是.
2. 设函数f(x)=ex+sinx,g(x)=ax,F(x)=f(x)-g(x).
(Ⅰ)若x=0是F(x)的极值点,求a的值;
(Ⅱ)当 a=1时,设P(x1,f(x1)), Q(x2, g(x 2))(x1>0,x2>0), 且PQ//x轴,求P、Q两点间的最短距离;
(Ⅲ):若x≥0时,函数y=F(x)的图象恒在y=F(-x)的图象上方,求实数a的取值范围.
解:(Ⅰ)F(x)= ex+sinx-ax,.
因为x=0是F(x)的极值点,所以.
又当a=2时,若x<0, ;若 x>0, .
∴x=0是F(x)的极小值点, ∴a=2符合题意.
(Ⅱ) ∵a=1, 且PQ//x轴,由f(x1)=g(x2)得:,所以.
令当x>0时恒成立.
∴x∈[0,+∞时,h(x)的最小值为h(0)=1.∴|PQ|min=1.
(Ⅲ)令
则.
因为当x≥0时恒成立,
所以函数S(x)在上单调递增,
∴S(x)≥S(0)=0当x∈[0,+∞时恒成立;
因此函数在上单调递增, 当x∈[0,+∞时恒成立.
当a≤2时,,在[0,+∞单调递增,即.
故a≤2时F(x)≥F(-x)恒成立.
1. (用到二阶导数,二次)
设函数.
⑴若,求的最小值;
⑵若当时,求实数的取值范围.
解:(1)时,,.
当时,;当时,.
所以在上单调减小,在上单调增加
故的最小值为
(2),
当时,,所以在上递增,
而,所以,所以在上递增,
而,于是当时, .
当时,由得
当时,,所以在上递减,
而,于是当时,,所以在上递减,
而,所以当时,.
综上得的取值范围为.
2. (第3问设计很好,2问是单独的,可以拿掉)已知函数,斜率为的直线与相切于点.
(Ⅰ)求的单调区间;
(Ⅱ)当实数时,讨论的极值点。
(Ⅲ)证明:.
解:(Ⅰ)由题意知:
………………………………2分
解得:; 解得:
所以在上单调递增,在上单调递减………………4分
(Ⅱ)=
得:.
若即,
+
-
+
极大值
极小值
此时的极小值点为,极大值点………………………………7分
若即,,则, 在上单调递增,无极值点.
若即,,
+
-
+
极大值
极小值
此时的极大值点为,极小值点.
综上述:
当时,的极小值点为,极大值点;
当时,无极值点;
当时,的极大值点为,极小值点.
1. (2011全国I文21,恒成立,一次,提出一部分再处理的技巧)
设函数.
⑴若a =,求的单调区间;
⑵若当≥0时≥0,求a的取值范围.
解:⑴时,,.
当时;当时,;
当时,.
故在,单调增加,在(-1,0)单调减少.
⑵.令,则.
①若,则当时,,为减函数,而,
从而当x≥0时≥0,即≥0,符合题意.
②若,则当时,,为减函数,而,
从而当时<0,即<0,不合题意.
综合得的取值范围为
2. (2011全国新理21,恒成立,反比例,提出公因式再处理的技巧,本题的创新之处是将一般的过定点(0,0)变为过定点(1,0),如果第2问范围变为则更间单)
已知函数在点处的切线方程为.
⑴求、的值;
⑵如果当,且时,,求的取值范围。
解:⑴,
依意意且,即,,解得,.
⑵由⑴知,所以.
设,则.
(注意h(x)恒过点(1,0),由上面求导的表达式发现讨论点0和1)
① 当,由,(变形难想,法二)
当时,.而,故
当时,,可得;
当x(1,+)时,<0,可得>0,
从而当x>0,且x1时,-(+)>0,即>+.
法二:的分子≤<0,∴.
②当0< k <1,由于当x(1,)时,(k-1)(x2 +1)+2x>0,故>0,而
=0,故当x(1,)时,>0,可得<0,不合题意.
③当k≥1,此时>0,则x(1,+)时,递增,,∴<0,不合题意.
综上,k的取值范围为(-,0]
1. (恒成立,讨论,较容易,但说明原理)已知函数.
(1)求函数的单调区间和极值;
(2)若对上恒成立,求实数的取值范围.
解:(1).
当时,,在上增,无极值;当时,,
在上减,在上增,∴有极小值,无极大值.
(2)
当时,在上恒成立,则是单调递增的,
则只需恒成立,所以.
当时,在上减,在上单调递增,所以当时,
这与恒成立矛盾,故不成立.
综上:.
1. (2010新课程理21,恒成立,讨论,二次,用到结论)
设函数.
⑴若,求的单调区间;
⑵若当时,求的取值范围.
解:命题意图:本题主要考查利用导数研究函数性质、不等式恒成立问题以及参数取值范围问题,考查分类讨论、转化与划归解题思想及其相应的运算能力.
⑴时,,.
当时,;当时,.故在单调减少,在单调增加.
⑵①当≤时,,
由⑴结论知≥,则,
故,从而当,即时,,
而,于是当时,,符合题意.
②时,由可得.(太难想,法二)
,
故当时,,而,于是当时,.
综合得的取值范围为.
法二:设,则,
令,得.
当,,在此区间上是增函数,∴≤,
∴在此区间上递增,∴≤,不合题意.
2. (恒成立,2010全国卷2理数,利用⑴结论,较难的变形讨论)
设函数.
⑴证明:当时,;
⑵设当时,,求a的取值范围.
解:本题主要考查导数的应用和利用导数证明不等式,考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
【点评】导数常作为高考的压轴题,对考生的能力要求非常高,它不仅要求考生牢固掌握基础知识、基本技能,还要求考生具有较强的分析能力和计算能力.估计以后对导数的考查力度不会减弱。作为压轴题,主要是涉及利用导数求最值解决恒成立问题,利用导数证明不等式等,常伴随对参数的讨论,这也是难点之所在.
1. 已知函数,且函数是上的增函数。
(1)求的取值范围;
(2)若对任意的,都有(e是自然对数的底),求满足条件的最大整数的值。
解析:(1)设,所以,得到.所以的取值范围为………2分
(2)令,因为是上的增函数,且,所以是上的增函数。…………………………4分
由条件得到(两边取自然对数),猜测最大整数,现在证明对任意恒成立。…………6分
等价于,………………8分
设,
当时,,当时,,
所以对任意的都有,即对任意恒成立,
所以整数的最大值为2.……………………………………………………14分
1. (2008山东卷21)
已知函数其中n∈N*,a为常数.
⑴当n=2时,求函数f(x)的极值;
⑵当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
解:⑴由已知得函数f(x)的定义域为{x|x>1},
当n=2时, 所以
①当a>0时,由f(x)=0得>1,<1,
此时=.
当x∈(1,x1)时,<0,f(x)单调递减;
当x∈(x1+∞)时,>0, f(x)单调递增.
②当a≤0时,<0恒成立,所以f(x)无极值.
综上所述,n=2时,
当a>0时,f(x)在处取得极小值,极小值为
当a≤0时,f(x)无极值.
⑵证法一:因为a=1,所以
①当n为偶数时,令
则)=1+>0(x≥2).
所以当x∈[2,+∞]时,g(x)单调递增,
又g(2)=0,因此≥g(2)=0恒成立,
所以f(x)≤x-1成立.
②当n为奇数时,要证≤x-1,由于<0,所以只需证ln(x-1) ≤x-1,
令h(x)=x-1-ln(x-1),则=1-≥0(x≥2),
所以,当x∈[2,+∞]时,单调递增,又h(2)=1>0,
所以当x≥2时,恒有h(x)>0,即ln(x-1)<x-1命题成立.
综上所述,结论成立.
证法二:当a=1时,
当x≤2,时,对任意的正整数n,恒有≤1,
故只需证明1+ln(x-1) ≤x-1.
令
则
当x≥2时,≥0,故h(x)在上单调递增,
因此,当x≥2时,h(x)≥h(2)=0,即1+ln(x-1) ≤x-1成立.
故当x≥2时,有≤x-1.
即f(x)≤x-1.
五、函数与导数性质的综合运用
1. (综合运用)
已知函数
⑴求函数的单调区间和极值;
⑵已知函数的图象与函数的图象关于直线对称,证明当时,
⑶如果,且,证明
解:本小题主要考查导数的应用,利用导数研究函数的单调性与极值等基础知识,考查运算能力及用函数思想分析解决问题的能力.
⑴,令=0,得.
当变化时,,的变化情况如下表
()
1
()
+
0
-
极大值
∴在()内是增函数,在()内是减函数;极大值.
⑵证明:由题意可知g(x)=f(2-x),∴g(x)=(2-x).
令F(x)=f(x)-g(x)=,则
当时,2x-2>0,从而
,从而在[1,+∞)是增函数。
又F(1)=F(x)>F(1)=0,即f(x)>g(x).
⑶证明:①若
②若
∴根据①②得
由⑵可知,>,则=,所以>,
从而>.因为,所以,
又由⑴可知函数在区间(-∞,1)内是增函数,所以>,即>2.
1. (2010天津理数21,综合运用)
已知函数
⑴求函数的单调区间和极值;
⑵已知函数对任意满足,证明:当时,
⑶如果,且,证明:
解:⑴∵=,∴=. (2分)
令=0,解得.
2
+
0
-
↗
极大值
↘
∴在内是增函数,在内是减函数. (3分)
∴当时,取得极大值=. (4分)
⑵证明:
,则
=. (6分)
当时,<0,>3,从而<0,
∴>0,在是增函数. (7分)
(8分)
⑶证明:∵在内是增函数,在内是减函数.
∴当,且,、不可能在同一单调区间内.
不妨设,由⑵可知,
又,∴.
∵,∴.
∵,且在区间内为增函数,
∴,即 (12分)
1. 已知函数
(1) 求函数的单调区间和极值;
(2) 若函数对任意满足,求证:当,
(3) 若,且,求证:
解:⑴∵=,∴=. (2分)
令=0,解得.
2
+
0
-
↗
极大值
↘
∴在内是增函数,在内是减函数. (3分)
∴当时,取得极大值=. (4分)
⑵证明:,,
∴=. (6分)
当时,<0,>4,从而<0,
∴>0,在是增函数.
(8分)
⑶证明:∵在内是增函数,在内是减函数.
∴当,且,、不可能在同一单调区间内.
不妨设,由⑵可知,
又,∴.
∵,∴.
∵,且在区间内为增函数,
∴,即
1. 已知函数,
(Ⅰ)若,求的单调区间;
(Ⅱ)对于任意的,比较与的大小,并说明理由.
解:(Ⅰ),,-----1分
①当时,在上恒成立,的递增区间为;------2分
②当时,的递增区间为;--------------3分
③当时,的递增区间为,递减区间为;--------4分
(Ⅱ)令,
,
令,在上恒成立,
当时,成立,在上恒成立,
在上单调递增,当时,恒成立,
当时,恒成立,
对于任意的时,,
又,,
,即.
2. (2011辽宁理21,利用2的对称)
已知函数.
⑴讨论的单调性;
⑵设,证明:当时,;(作差)
⑶若函数的图像与x轴交于A、B两点,线段AB中点的横坐标为,证明:.
解:⑴
①若单调增加.
②若
且当
所以单调增加,在单调减少.
⑵设函数则
当.
故当,
⑶由⑴可得,当的图像与x轴至多有一个交点,
故,从而的最大值为
不妨设
由⑵得
从而
由⑴知,
1. (恒成立,思路不常见)
已知函数,其中为实数.
(1)当时,求曲线在点处的切线方程;
(2)是否存在实数,使得对任意,恒成立?若不存在,请说明理由,若存在,求出的值并加以证明.
解:⑴时,,,
,又,所以切线方程为.
⑵①当时,,则
令,,
再令,
当时,∴在上递减,
∴当时,,
∴,所以在上递增,,所以
②时,,则
由①知当时,在上递增
当时,,
所以在上递增,∴,∴;
由①②得.
1. 已知函数,在区间上有最大值4,最小值1,设.
(Ⅰ)求的值;
(Ⅱ)不等式在上恒成立,求实数的范围;
(Ⅲ)方程有三个不同的实数解,求实数的范围.
解:(Ⅰ)(1)
当时,上为增函数
故
当上为减函数
故
即. .
(Ⅱ)方程化为
,令,
∵ ∴ 记∴ ∴
(Ⅲ)方程化为
,
令, 则方程化为 ()
∵方程有三个不同的实数解,
∴由的图像知,
有两个根、,
且 或 ,
记
则 或 ∴
1. 已知函数, 设
(1)是否存在唯一实数,使得,若存在,求正整数m的值;若不存在,说明理由。
(2)当时,恒成立,求正整数n的最大值。
解:(1)由得
则因此在内单调递增。……………4分
因为,,
即存在唯一的根,于是 ……………6分
(2)由得,且恒成立,由第(1)题知存在唯一的实数,使得,且当时,,;当时,,因此当时,取得最小值 ……………9分
由,得 即 于是
又由,得,从而,故正整数n的最大值为3。………12分
2. (第3问难想)已知函数,其中e是自然数的底数,。
(1) 当时,解不等式;
(1) 若在[-1,1]上是单调增函数,求的取值范围;
(2) 当时,求整数k的所有值,使方程在[k,k+1]上有解。
⑴因为,所以不等式即为,
又因为,所以不等式可化为,
所以不等式的解集为.………………………………………4分
⑵,
①当时,,在上恒成立,当且仅当时
取等号,故符合要求;………………………………………………………6分
②当时,令,因为,
所以有两个不相等的实数根,,不妨设,
因此有极大值又有极小值.
若,因为,所以在内有极值点,
故在上不单调.………………………………………………………8分
若,可知,
因为的图象开口向下,要使在上单调,因为,
必须满足即所以.
综上可知,的取值范围是.………………………………………10分
⑶当时, 方程即为,由于,所以不是方程的解,
所以原方程等价于,令,
因为对于恒成立,
所以在和内是单调增函数,……………………………13分
又,,,,
所以方程有且只有两个实数根,且分别在区间和上,
所以整数的所有值为.………………………………………………………16分
1. (2011高考,单调性应用,第2问难)
已知a、b是实数,函数 和是的导函数,若在区间I上恒成立,则称和在区间I上单调性一致.
(1)设,若函数和在区间上单调性一致,求实数b的取值范围;
(2)设且,若函数和在以a,b为端点的开区间上单调性一致,求|a-b|的最大值.
解:
⑴因为函数和在区间上单调性一致,
所以,
即
即实数b的取值范围是
⑵由
若,则由,,和在区间上不是单调性一致,所以.
;又.
所以要使,只有
,
取,当时,
因此
当时,因为,函数和在区间(b,a)上单调性一致,所以,
即,
设,考虑点(b,a)的可行域,函数的斜率为1的切线的切点设为
则;
当时,因为,函数和在区间(a, b)上单调性一致,所以,
即,
当时,因为,函数和在区间(a, b)上单调性一致,所以,
即而x=0时,不符合题意,
当时,由题意:
,
综上可知,。
1. (2010湖南文数,另类区间)
已知函数其中a<0,且a≠-1.
(Ⅰ)讨论函数的单调性;
(Ⅱ)设函数(e是自然数的底数)。是否存在a,使在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
79. (2008辽宁理22,第2问无从下手,思路太难想)
设函数.
⑴求的单调区间和极值;
⑵是否存在实数,使得关于的不等式的解集为?若存在,求的取值范围;若不存在,试说明理由.
说明:本小题主要考查函数的导数,单调性,极值,不等式等基础知识,考查综合利用数学知识分析问题、解决问题的能力.满分14分.
解:⑴.
故当时,,时,.
所以在单调递增,在单调递减.
由此知在的极大值为,没有极小值.
⑵①当时,由于,
故关于的不等式的解集为.
②当时,由知,其中为正整数,且有.
又时,.且.
取整数满足,,且,
则,
即当时,关于的不等式的解集不是.
综合①②知,存在,使得关于的不等式的解集为,且的取值范围为.
80. (第二问较难)
设函数,,是的一个极大值点.
⑴若,求的取值范围;
⑵当是给定的实常数,设是的3个极值点,问是否存在实数,可找到,使得的某种排列(其中=)依次成等差数列?若存在,求所有的及相应的;若不存在,说明理由.
解:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识.
(Ⅰ)时,,
,
令,,
设是的两个根,
(1)当或时,则不是极值点,不合题意;
(2)当且时,由于是的极大值点,故
,即,
(Ⅱ)解:,
令,
,
于是,假设是的两个实根,且
由(Ⅰ)可知,必有,且是的三个极值点,
则,
假设存在及满足题意,
(1)当等差时,即时,
则或,
于是,即
此时
或
(2)当时,则或
①若,则,
于是,
即
两边平方得,
于是,此时,
此时=
②若,则,
于是,
即两边平方得,
于是,此时
此时
综上所述,存在b满足题意,
当b=-a-3时,,
时,,
时,.
81. 已知函数,,记
(Ⅰ)求的单调区间;
(Ⅱ)当时,若,比较:与的大小;
(Ⅲ)若的极值为,问是否存在实数,使方程有四个不同实数根?若存在,求出实数的取值范围;若不存在,请说明理由。
解:(Ⅰ)的定义域为(0,+∞), 又
, 当时,>0恒成立
∴在(0,+∞)上单调递增; 令得
当时,若, ∴在(0,)上单调递减;
若,,∴在(,+∞)上单调递增
故时,增区间为;
时,增区间为,减区间为(0,)。 ……4分
(Ⅱ)令,
则,所以在[1,+∞)
上单调递增,∴,∴.
(Ⅲ)由(Ⅰ)知仅当时,在=处取得极值
由可得=2,方程为
,令,得...
由方程有四个不同的根,得方程有两个不同的正根,
令,当直线与曲线相切时,,得切点坐标(3,) ∴切线方程为,其在y轴上截距为;当直线在轴上截距时,和在y轴右侧有两个不同交点,所以k的取值范围为(,0).
(注:也可用导数求解)
六、导数应用题
82. 某工厂生产某种儿童玩具,每件玩具的成本为30元,并且每件玩具的加工费为t元(其中t为常数,且2≤t≤5),设该工厂每件玩具的出厂价为x元(35≤x≤41),根据市场调查,日销售量与ex(e为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
(1)求该工厂的日利润y(元)与每件玩具的出厂价x元的函数关系式;
(2)当每件玩具的日售价为多少元时,该工厂的利润y最大,并求y的最大值.
解:(1)设日销售量为,则=10,∴k=10 e40.则日销售量为,
∴日利润y=(x-30-t)·.∴y=,其中35≤x≤41.
(2)y′=,令y′=0得x=31+t.
①当2≤t≤4时,33≤31+t≤35.∴当35≤x≤41时,y′≤0.
∴当x=35时,y取最大值,最大值为10(5-t)e5.
②当4
查看更多