- 2021-04-20 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014年版高考数学理18解三角形应用举例二轮考点专练
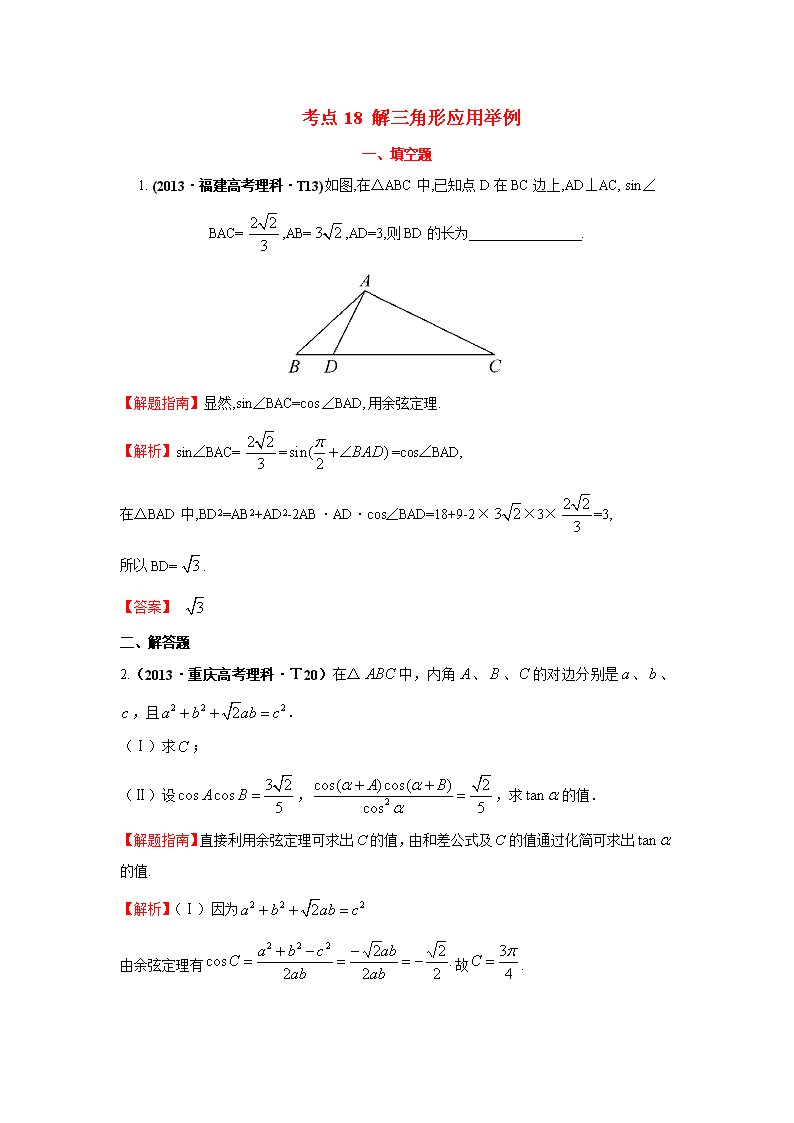
考点18 解三角形应用举例 一、填空题 1. (2013·福建高考理科·T13)如图,在△ABC中,已知点D在BC边上,AD⊥AC, sin∠BAC=,AB=,AD=3,则BD的长为 . 【解题指南】显然,sin∠BAC=cos∠BAD,用余弦定理. 【解析】sin∠BAC===cos∠BAD, 在△BAD中,BD2=AB2+AD2-2AB·AD·cos∠BAD=18+9-2××3×=3, 所以BD=. 【答案】 二、解答题 2.(2013·重庆高考理科·T20)在△中,内角、、的对边分别是、、,且. (Ⅰ)求; (Ⅱ)设,,求的值. 【解题指南】直接利用余弦定理可求出的值,由和差公式及的值通过化简可求出的值. 【解析】(Ⅰ)因为 由余弦定理有故. (Ⅱ)由题意得 因此 ① 因为,所以 因为即 解得 由①得, 解得或. 3. (2013·重庆高考文科·T18)在△ABC中,内角A,B,C的对边分别是a,b,c,且a2=b2+c2+ab. (Ⅰ)求; (Ⅱ)设a=,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值. 【解题指南】直接利用余弦定理可求出的值,再利用正弦定理求解S+3cosBcosC的最大值,并指出此时的值. 【解析】(Ⅰ)由余弦定理得 又因为,所以 (Ⅱ)由(Ⅰ)得又有正弦定理及得 因此, 所以,当,即时, 取最大值 4. (2013·山东高考理科·T17)设△ABC的内角A,B,C所对的边分别为a,b,c,且a+c=6,b=2,cosB=. (1)求a,c的值; (2)求sin(A-B)的值. 【解题指南】(1)先由余弦定理可得到ac的关系式,再和已知a+c=6联立方程,可得a,c的值;(2)由知,需先求出sinA,sinB,cosA,cosB的值,可先利用同角三角函数基本关系式求出sinB,然后由正弦定理求出sinA,进而求得cosA,从而本题得解. 【解析】(1)由与余弦定理得,得 又a+c=6,b=2,cosB=,所以ac=9,解得a=3,c=3. (2)在△ABC中,, 由正弦定理得. 因为a=c,所以A为锐角. 所以. 因此. 5.(2013·福建高考文科·T21)如图,在等腰直角中,, ,点在线段上. (I)若,求的长; (II)若点在线段上,且,问:当取何值时,的面积最小?并求出面积的最小值. 【解题指南】由等腰知,此时,可解;第(II)问,按“求什么设什么”列式求解,将面积表达式写出,利用三角函数计算公式求解。 【解析】(Ⅰ)在中,,,, 由余弦定理得,,得,解得或. (Ⅱ)设,, 在中,由正弦定理,得, 所以, 同理 故 因为,,所以当时,的最大值为,此时的面积取到最小值.即时,的面积的最小值为. 6.(2013·江苏高考数学科·T18)如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量, ,. (1)求索道AB的长. (2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短? (3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内? 【解题指南】(1)利用正弦定理确定出AB的长.(2)先设再建立时间t与甲、乙间距离d的函数关系式,利用关系式求最值.(3)利用条件“使两位游客在C处互相等待的时间不超过3分钟” 建立不等式求解. 【解析】(1)在△ABC中,因为cosA=,cosC=,所以sinA=,sinC=. 从而sinB=sin[π-(A+C)] =sin(A+C)=sinAcosC+cosAsinC =, 由正弦定理=,得 AB=×sinC= =1040(m). 所以索道AB的长为1040m. (2)假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130tm,所以由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×=200(37t2-70t+50), 因0≤t≤,即0≤t≤8, 故当t= (min)时,甲、乙两游客距离最短. (3)由正弦定理=,得BC=×sinA==500(m). 乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710m才能到达C. 设乙步行的速度为vm/min,由题意得-3≤ ≤3,解得 所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在[,] (单位:m/min)范围内.查看更多