高考全品原创模拟卷数学文科
2017年高考全品原创模拟卷(一)
数学(文科)
时间:120分钟 满分:150
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={-1,0,1,2,3},B={x|x2(2-x)>0},则A∩(∁RB)=( )
A.{-1,1} B.{2,3} C.{0,3} D.{0,2,3}
2.设z=a+(a+1)i(a∈R),i为虚数单位,若z(2-i)为实数,则a=( )
A.-2 B.-1 C.0 D.1
3.若函数f(x)=(2a+1)x-在(3,+∞)上是增函数,则实数a的取值范围是 ( )
A. B.
C.∪ D.∪
4.在区间[-4,4]上任取实数a,则关于x的方程x++1=a有实数解的概率为( )
A. B. C. D.
5.已知α=60°,若点P(a,b)(a>0,b>0)是α终边上一点,则双曲线-=1的离心率为( )
A.2 B. C. D.
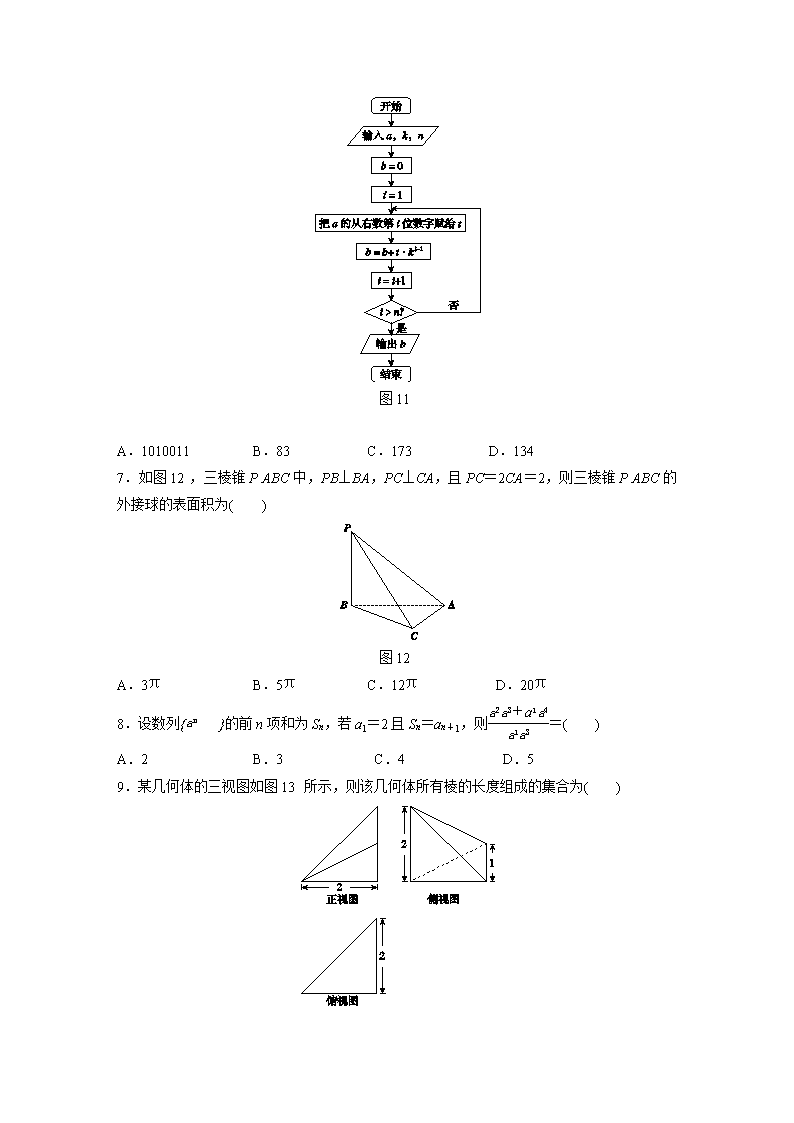
6.执行如图11所示的程序框图,若输入的k,a,n分别为8,123,3,则输出的b=( )
图11
A.1010011 B.83 C.173 D.134
7.如图12,三棱锥PABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥PABC的外接球的表面积为( )
图12
A.3π B.5π C.12π D.20π
8.设数列的前n项和为Sn,若a1=2且Sn=an+1,则=( )
A.2 B.3 C.4 D.5
9.某几何体的三视图如图13所示,则该几何体所有棱的长度组成的集合为( )
图13
A. B.
C. D.
10.直线x-y-2=0与抛物线y2=4x及圆E:x2+y2-4x-2=0从上到下的交点依次为点A,B,C,D,则+的值为( )
A.4-2 B.2 C.3 D.4-6
11.设不等式组表示的平面区域为D,已知点A(-2,0),B(x,y),O为坐标原点,且点B∈D,记,的夹角为θ,则2(1+cos 2θ)的取值范围是( )
A. B. C. D.
12.已知函数f(x)=x3-2kx2-x+1有两个不同的极值点x1,x2(x1<1
b>0)的左、右焦点分别为F1,F2,设点A(a,b),且==2.
(1)求椭圆C的方程.
(2)已知四边形MNPQ的四个顶点均在曲线C上,且MQ∥NP,MQ⊥x轴,若直线MN和直线QP交于点S(4,0).判断四边形MNPQ两条对角线的交点是否为定点?若是,求出定点坐标;若不是,请说明理由.
21.(本小题满分12分)已知函数f(x)=2xex.
(1)过点(-4,0)作曲线y=f(x)的切线l,求切线l的方程;
(2)若实数a满足(a-1)(ea-1)>0,求证:对任意x∈(0,+∞),a[f(x)-a(e2x-1)]<0恒成立.
请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.
22.(本小题满分10分)选修44:坐标系与参数方程
以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ2(1+3sin2θ)=4.
(1)求曲线C的参数方程;
(2)若曲线C与x轴的正半轴及y轴的正半轴分别交于点A,B,在曲线C上任取一点P,且点P在第一象限,求四边形OAPB面积的最大值.
23.(本小题满分10分)选修45:不等式选讲
已知函数f(x)=|x|-|x-2|.
(1)若方程f(x)=a有无数个实数解,求实数a的取值集合M;
(2)若正数a,b满足a2+b2∈M,求证:a+b≥2ab.
2017年高考全品原创模拟卷(二)
数学(文科)
时间:120分钟 满分:150
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={x|x2+2x-3≤0},集合B={x|y=log2(3-x)},则B∩(∁RA)=( )
A.[-3,1] B.(-∞,-3)∪(1,3)
C.(-∞,-3) D.R
2.已知i是虚数单位,复数z(2-3i)的共轭复数为1+i,则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.《九章算术》中有这样一个问题:某粮仓内自左至右依次有一至十共十座粮囤,粮囤自左至右积黍依次增等担,前九囤共储黍二百七十担,第六囤、第八囤共储黍八十担,则第十囤储黍担数为( )
A.45 B.50 C.55 D.60
4.执行如图21所示的程序框图,则输出S的值为( )
图21
A.16 B.12 C.-4 D.-36
5.已知函数f(x)=若命题:∀x1,x2∈R且x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0为真命题,则实数a的取值范围为( )
A. B. C. D.
6.已知一个组合体的三视图如图22所示,则该组合体的表面积为( )
图22
A.4π+12π B.4π+8π C. D.8π
7.已知角α是第二象限角,sin α=,角β的顶点在坐标原点O,始边为x轴的非负半轴,终边过点P(12,-5),则sin(α+β)=( )
A.- B.- C. D.
8.某中学某位班主任为研究该班学生物理成绩与数学成绩的相关性,随机抽取该班6位同学高一上学期期中考试数学成绩和相应的物理成绩如下表:
数学成绩xi
90
100
115
125
130
142
物理成绩yi
60
65
69
78
85
由这些样本数据算得变量x与y满足线性回归方程=0.47x+17.01,但由于某种原因该表中某位同学的物理成绩被污损,根据回归方程和表中数据可得污损的物理成绩为a,数学成绩的中位数为b,若直线l1:cx+(71-a)y+4=0与直线l2:(b-119)x-cy+2=0平行,则实数c的值为( )
A.±2 B.±4.65 C.-2 D.0
9.已知实数x,y满足则z=的取值范围为( )
A. B. C. D.
10.已知抛物线E:y2=4x上一动点P在准线上的投影为Q,M是圆N:x2+y2+2x+4y+4=0上的动点,则|PQ|+|PM|的最小值为( )
A.2 B.2-1 C.3 D.2+1
11.已知F1,F2分别是双曲线E:-=1(a>0,b>0)的左、右焦点,双曲线E的虚轴长为12,P是双曲线E所在平面内一点,线段PF1的中点在双曲线右支上,F1关于F2对称的点为Q,若|PF1|-|PQ|=32,则该双曲线的离心率为( )
A. B. C. D.
12.已知函数f(x)=-ax+a-e恰有两个不同的零点,则实数a的取值范围为( )
A.(-∞,0) B.(1,e) C.(0,+∞) D.(-∞,+∞)
第Ⅱ卷(非选择题 共90分)
本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22题~第23题为选考题,考生根据要求作答.
二、填空题:本大题共4小题,每小题5分,共20分.
13.某大学某个专业在某省只录取一个学生,该省高考成绩相同的甲、乙、丙三位同学同时报考该大学的该专业,录取时随机录取,已知甲同学被录取的概率是乙同学被录取的概率的2倍,是丙同学被录取的概率的,则丙同学没被该校该专业录取的概率为________.
14.已知a,b是非零向量,a在b方向上的投影为-2,|a|=2,a⊥(a+2b),则|2a-b|=________.
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,若=,ab=4,则△ABC的面积为________.
16.已知定义域为R的函数f(x)满足对任意x∈R都有f(x)-f(-x)=0,当x≥0时,f(x)=log2(x+1),则不等式f(x+1)>2的解集为________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知数列{an}的前n项和为Sn,an=(Sn+1).
(1)求数列{an}的通项公式;
(2)已知bn=(3n-2)an,求数列{bn}的前n项和Tn的取值范围.
18.(本小题满分12分)4月7日是世界健康日,北京某运动器材与服饰销售公司为了制定其销售策略,在北京市随机抽取了40名市民对其每天的锻炼时间(锻炼时间均在140分钟以内)
进行调查,根据调查结果绘制的锻炼时间(单位:分钟)的频率分布直方图如图23所示.
图23
(1)根据频率分布直方图计算这40人每天的锻炼时间的中位数;
(2)从锻炼时间在[20,60)的人中选2人,求恰好1人锻炼时间在[20,40)的概率.
19.(本小题满分12分)已知四边形ABCD为等腰梯形,AB∥CD,∠ABC=60°,AD=CD=2,四边形ACMN是直角梯形,CM∥AN,AN⊥AC,平面ACMN⊥平面ABCD,CM=2AN=4,E是AN的中点.
(1)求证:BC⊥EM;
(2)求点M到平面BCE的距离.
图24
20.(本小题满分12分)已知A,B,F2分别是离心率为的椭圆E:+=1(a>b>0)的上顶点、右顶点、右焦点,·=-11.
(1)求椭圆E的方程;
(2)过F2作直线l与椭圆E交于点M,N,求|MN|的最小值,并求出取得最小值时直线l的方程.
21.(本小题满分12分)已知函数f(x)=ex-mx2+(m-e)x(m∈R).
(1)若函数f(x)的图像在点(0,f(0))处的切线与直线2x-y+2=0垂直,求实数m的值;
(2)若x≥1时,f′(x)≥0恒成立,求实数m的取值范围.
请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.
22.(本小题满分10分)选修44:坐标系与参数方程
在平面直角坐标系xOy和极坐标系中,极点与原点重合,极轴与x轴非负半轴重合,直线l的参数方程为(t为参数),曲线C的极坐标方程为ρ2-4ρcos θ-2ρsin θ+1=0.
(1)将直线l的参数方程化为普通方程,将曲线C的极坐标方程化为直角坐标方程;
(2)判断直线l与曲线C的位置关系,若直线l与曲线C相交,设交点为A,B,求|AB|.
23.(本小题满分10分)选修45:不等式选讲
已知函数f(x)=|2x-4|+x+3.
(1)求函数f(x)的最小值M;
(2)已知a,b∈R+,a+2b=M,求+的最小值.
2017年高考全品原创模拟卷(三)
数学(文科)
时间:120分钟 满分:150
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合M={-1,0,1},N=yy=1+2sin,x∈M,则集合M∩N子集的个数是( )
A.4 B.3 C.2 D.1
2.复数z=(i为虚数单位)的共轭复数的模是( )
A. B. C.2 D.5
3.下表提供了某厂节能降耗技术改造后在生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据:
x
3
4
5
6
y
2.5
t
4
4.5
根据上表提供的数据,求出y关于x的线性回归方程为=0.7x+0.35,那么表中t的值为( )
A.3 B.3.15 C.3.5 D.3.75
4.用若干个棱长为 1 的正方体拼成一个几何体,它的正视图,侧视图都是图31,则这个几何体体积的最小值是( )
A.5 B.7 C.9 D.11
图31
5.执行如图32所示的程序框图,则输出的S值为( )
图32
A.2+ B.2- C.3+ D.3-
6.将边长为6和8的长方形ABCD沿它的一条对角线AC折成二面角BACD,则经过四点A,B,C,D的球的内接正方体的全面积为( )
A.100 B.200 C.100π D.200π
7.设Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,设此等比数列的公比为q,则4q3=( )
A.-2 B.-1 C.1 D.2
图33
8.如图33,在△ABC中,CA=4,CB=6.若点G为△ABC的重心,则·的值为( )
A. B. C. D.
9.已知点P是抛物线y2= 2x上的动点,点P在y轴上的射影是M,点A的坐标是A,4,则| PA | + | PM |的最小值是( )
A. B.4 C. D.5
10.如果sin acos b=,则cos asin b的取值范围是( )
A. B. C. D.
11.不等式2ax2-x-2≤1在x∈[-1,1]上恒成立,则实数a的取值范围是( )
A. B.(-∞,1]
C. D.
12.过曲线y=(a>0)上任意一点处的切线与两坐标轴构成的三角形的面积是( )
A. 2a2 B.a2 C.2a D.a
第Ⅱ卷(非选择题 共90分)
本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22题~第23题为选考题,考生根据要求作答.
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知3t+t3=135,[x]表示不超过实数x的最大整数,则[t]=________.
14.设点P是圆x2+y2=4上的任一点,定点D的坐标为(8,0).当点P在圆上运动时,线段PD的中点M的轨迹方程是________.
15.设z=y-2x,其中实数x,y满足+≤1,则z的最大值是________.
16.若甲、乙、丙三人的考试成绩各不相同,且满足:
(1)如果乙的成绩不是最高,那么甲的成绩最低;
(2)如果丙的成绩不是最低,那么甲的成绩最高.
如此判断,三人中成绩最低的应该是________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)在△ABC中,内角C所对的边长为c,△ABC的面积为S,且tantan+=1.
(1)求△ABC的内角C的值;
(2)求证:c2≥4S.
18.(本小题满分12分)某房地产公司的新建小区有A,B两种户型住宅,其中A户型住宅的每套面积为100平方米,B户型住宅的每套面积为80平方米.该公司准备从两种户型中各拿出10套试销售,下表是这20套住宅每平方米的销售价格(单位:万元/平方米).
1
2
3
4
5
6
7
8
9
10
A户型
0.7
1.3
1.1
1.4
1.1
0.9
0.8
0.8
1.3
0.9
B户型
1.2
1.6
2.3
1.8
1.4
2.1
1.4
1.2
1.7
1.3
(1)根据上表数据,完成如图34所示的茎叶图,并分别求出A,B两类户型住宅每平方米销售价格的中位数.
(2)若该公司决定:通过抽签方式进行试销售,抽签活动按A,B户型分成两组,购房者从中任选一组参与抽签(只有一次机会),并根据抽签结果和自己的购买力决定是否购买(仅当抽签结果超过购买力时,放弃购买).
现某居民获得优先抽签权,且他的购买力最多为120万元,为了使其购房成功概率更大,请你向其推荐应当参加哪个户型的抽签活动,并为他估计此次购房的平均单价(单位:万元/平方米).
图34
19.(本小题满分12分)如图35,在三棱柱ABCA1B1C1中,AC=1,BC=2,AC⊥BC, CC1=1,∠ACC1=60°,D,E,F分别为棱AA1,A1B1,AC的中点.
(1)求证:EF∥平面BCC1B1;
(2)若异面直线AA1与EF所成的角为45°,求三棱锥C1DCB的体积.
图35
20.(本小题满分12分)已知F,0为抛物线y2=2px(p>0)的焦点,点N(x0,y0)(y0>0)为其上一点,点M与点N关于x轴对称,直线l与抛物线交于异于M,N的A,B两点,且|NF|=,kNA·kNB=-2(kNA,kNB分别为直线NA,NB的斜率).
(1)求抛物线方程和N点坐标.
(2)判断是否存在直线l使得△MAB的面积最小?若存在,求出直线l的方程和△MAB面积的最小值;若不存在,说明理由.
21.(本小题满分12分)已知f(x)=ax+ln x,g(x)=ex.
(1)当a≤0时,求f(x)的单调区间;
(2)若不等式g(x)<有解,求实数m的取值范围.
请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.
22.(本小题满分10分)选修44:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线l的极坐标方程为ρsin=,曲线C的参数方程是(α是参数).
(1)求直线l的直角坐标方程及曲线C的普通方程;
(2)求曲线C上的点到直线l的最小距离.
23.(本小题满分10分)选修45:不等式选讲
对于实数x∈,f=+.
(1)当不等式f(x)≥2t-1恒成立时,求t的最大值;
(2)在(1)的条件下,当t取最大值时求不等式|x+t|+|x-2|≥5的解集.