2012年湖南省高考数学试卷（理科）

2012年湖南省高考数学试卷（理科）

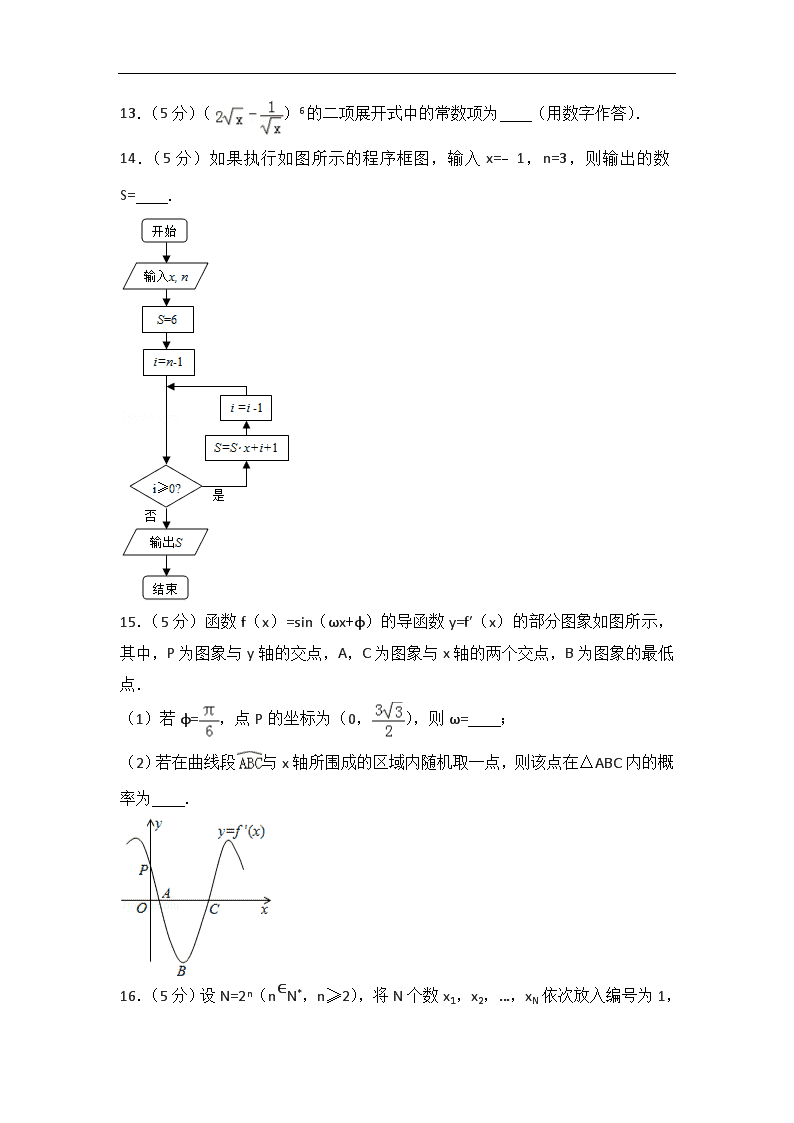
‎2012年湖南省高考数学试卷（理科）‎ ‎　‎ 一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）设集合M={﹣1，0，1}，N={x|x2≤x}，则M∩N=（　　）‎ A．{0} B．{0，1} C．{﹣1，1} D．{﹣1，0，1}‎ ‎2．（5分）命题“若α=，则tanα=1”的逆否命题是（　　）‎ A．若α≠，则tanα≠1 B．若α=，则tanα≠1‎ C．若tanα≠1，则α≠ D．若tanα≠1，则α=‎ ‎3．（5分）某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是（　　）‎ A． B． C． D．‎ ‎4．（5分）设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x﹣85.71，则下列结论中不正确的是（　　）‎ A．y与x具有正的线性相关关系 B．回归直线过样本点的中心（，）‎ C．若该大学某女生身高增加1cm，则其体重约增加0.85kg D．若该大学某女生身高为170cm，则可断定其体重必为58.79kg ‎5．（5分）已知双曲线C：的焦距为10，点P（2，1）在C的渐近线上，则C的方程为（　　）‎ A． B．‎ C． D．‎ ‎6．（5分）函数f（x）=sinx﹣cos（x+）的值域为（　　）‎ A．[﹣2，2] B．[﹣，] C．[﹣1，1] D．[﹣，]‎ ‎7．（5分）在△ABC中，AB=2，AC=3，•=1，则BC=（　　）‎ A． B． C．2 D．‎ ‎8．（5分）已知两条直线l1：y=m和l2：y=（m＞0），l1与函数y=|log2x|的图象从左至右相交于点A，B，l2与函数y=|log2x|的图象从左至右相交于点C，D．记线段AC和BD在X轴上的投影长度分别为a，b，当m变化时，的最小值为（　　）‎ A．16 B．8 C．8 D．4‎ ‎　‎ 二、填空题（共8小题，考生作答7小题，每小题0分，满分35分，9,10,11三题任选两题作答；12～16必做题）‎ ‎9．在直角坐标系xoy 中，已知曲线C1：（t为参数）与曲线C2：（θ为参数，a＞0 ）有一个公共点在X轴上，则a等于　　．‎ ‎10．（5分）不等式|2x+1|﹣2|x﹣1|＞0的解集为　　．‎ ‎11．（5分）如图，过点P的直线与圆⊙O相交于A，B两点．若PA=1，AB=2，PO=3，则圆O的半径等于　　．‎ ‎12．（5分）已知复数z=（3+i）2（i为虚数单位），则|z|=　　．‎ ‎13．（5分）（）6的二项展开式中的常数项为　　（用数字作答）．‎ ‎14．（5分）如果执行如图所示的程序框图，输入x=﹣1，n=3，则输出的数S=　　．‎ ‎15．（5分）函数f（x）=sin（ωx+φ）的导函数y=f′（x）的部分图象如图所示，其中，P为图象与y轴的交点，A，C为图象与x轴的两个交点，B为图象的最低点．‎ ‎（1）若φ=，点P的坐标为（0，），则ω=　　；‎ ‎（2）若在曲线段与x轴所围成的区域内随机取一点，则该点在△ABC内的概率为　　．‎ ‎16．（5分）设N=2n（n∈N*，n≥2），将N个数x1，x2，…，xN 依次放入编号为1，2，…，N的N个位置，得到排列P0=x1x2…xN．将该排列中分别位于奇数与偶数位置的数取出，并按原顺序依次放入对应的前和后个位置，得到排列P1=x1x3…xN﹣1x2x4…xN，将此操作称为C变换，将P1分成两段，每段个数，并对每段作C变换，得到P2，当2≤i≤n﹣2时，将Pi分成2i段，每段个数，并对每段作C变换，得到Pi+1，例如，当N=8时，P2=x1x5x3x7x2x6x4x8，此时x7位于P2中的第4个位置．‎ ‎（1）当N=16时，x7位于P2中的第　　个位置；‎ ‎（2）当N=2n（n≥8）时，x173位于P4中的第　　个位置．‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示．‎ 一次性购物量 ‎1至4件 ‎5 至8件 ‎9至12件 ‎13至16件 ‎17件及以上 顾客数（人）‎ x ‎30‎ ‎25‎ y ‎10‎ 结算时间（分钟/人）‎ ‎1‎ ‎1.5‎ ‎2‎ ‎2.5‎ ‎3‎ 已知这100位顾客中的一次购物量超过8件的顾客占55%．‎ ‎（Ⅰ）确定x，y的值，并求顾客一次购物的结算时间X的分布列与数学期望；‎ ‎（Ⅱ）若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2.5分钟的概率．（注：将频率视为概率）‎ ‎18．（12分）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是CD的中点．‎ ‎（Ⅰ）证明：CD⊥平面PAE；‎ ‎（Ⅱ）若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P﹣ABCD的体积．‎ ‎19．（12分）已知数列{an}的各项均为正数，记A（n）=a1+a2+…+an，B（n）=a2+a3+…+an+1，C（n）=a3+a4+…+an+2，n=1，2，…．‎ ‎（1）若a1=1，a2=5，且对任意n∈N*，三个数A（n），B（n），C（n）组成等差数列，求数列{an}的通项公式．‎ ‎（2）证明：数列{an}是公比为q的等比数列的充分必要条件是：对任意n∈N*，三个数A（n），B（n），C（n）组成公比为q的等比数列．‎ ‎20．（13分）某企业接到生产3000台某产品的A，B，C三种部件的订单，每台产品需要这三种部件的数量分别为2，2，1（单位：件）．已知每个工人每天可生产A部件6件，或B部件3件，或C部件2件．该企业计划安排200名工人分成三组分别生产这三种部件，生产B部件的人数与生产A部件的人数成正比，比例系数为K（K为正整数）．‎ ‎（1）设生产A部件的人数为x，分别写出完成A，B，C三种部件生产需要的时间；‎ ‎（2）假设这三种部件的生产同时开工，试确定正整数K的值，使完成订单任务的时间最短，并给出时间最短时具体的人数分组方案．‎ ‎21．（13分）在直角坐标系xoy中，曲线C1上的点均在C2：（x﹣5）2+y2=9外，且对C1上任意一点M，M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值．‎ ‎（Ⅰ）求曲线C1的方程 ‎（Ⅱ）设P（x0，y0）（y0≠±3）为圆C2外一点，过P作圆C2的两条切线，分别于曲线C1相交于点A，B和C，D．证明：当P在直线x=﹣4上运动时，四点A，B，C，D的纵坐标之积为定值．‎ ‎22．（13分）已知函数f（x）=eax﹣x，其中a≠0．‎ ‎（1）若对一切x∈R，f（x）≥1恒成立，求a的取值集合．‎ ‎（2）在函数f（x）的图象上取定两点A（x1，f（x1）），B（x2，f（x2）（x1＜x2），记直线AB的斜率为K，问：是否存在x0∈（x1，x2），使f′（x0）＞k成立？若存在，求x0的取值范围；若不存在，请说明理由．‎ ‎　‎ ‎2012年湖南省高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）（2012•湖南）设集合M={﹣1，0，1}，N={x|x2≤x}，则M∩N=（　　）‎ A．{0} B．{0，1} C．{﹣1，1} D．{﹣1，0，1}‎ ‎【分析】求出集合N，然后直接求解M∩N即可．‎ ‎【解答】解：因为N={x|x2≤x}={x|0≤x≤1}，M={﹣1，0，1}，‎ 所以M∩N={0，1}．‎ 故选B．‎ ‎　‎ ‎2．（5分）（2012•湖南）命题“若α=，则tanα=1”的逆否命题是（　　）‎ A．若α≠，则tanα≠1 B．若α=，则tanα≠1‎ C．若tanα≠1，则α≠ D．若tanα≠1，则α=‎ ‎【分析】原命题为：若a，则b．逆否命题为：若非b，则非a．‎ ‎【解答】解：命题：“若α=，则tanα=1”的逆否命题为：若tanα≠1，则α≠．‎ 故选C．‎ ‎　‎ ‎3．（5分）（2012•湖南）某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是（　　）‎ A． B． C． D．‎ ‎【分析】由图可知，此几何体为组合体，对照选项分别判断组合体的结构，能吻合的排除，不吻合的为正确选项 ‎【解答】解：依题意，此几何体为组合体，若上下两个几何体均为圆柱，则俯视图为A 若上边的几何体为正四棱柱，下边几何体为圆柱，则俯视图为B；‎ 若俯视图为C，则正视图中应有虚线，故该几何体的俯视图不可能是C 若上边的几何体为底面为等腰直角三角形的直三棱柱，下面的几何体为正四棱柱时，俯视图为D；‎ 故选C ‎　‎ ‎4．（5分）（2012•湖南）设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x﹣85.71，则下列结论中不正确的是（　　）‎ A．y与x具有正的线性相关关系 B．回归直线过样本点的中心（，）‎ C．若该大学某女生身高增加1cm，则其体重约增加0.85kg D．若该大学某女生身高为170cm，则可断定其体重必为58.79kg ‎【分析】根据回归方程为=0.85x﹣85.71，0.85＞0，可知A，B，C均正确，对于D回归方程只能进行预测，但不可断定．‎ ‎【解答】解：对于A，0.85＞0，所以y与x具有正的线性相关关系，故正确；‎ 对于B，回归直线过样本点的中心（，），故正确；‎ 对于C，∵回归方程为=0.85x﹣85.71，∴该大学某女生身高增加1cm，则其体重约增加0.85kg，故正确；‎ 对于D，x=170cm时，=0.85×‎ ‎170﹣85.71=58.79，但这是预测值，不可断定其体重为58.79kg，故不正确 故选D．‎ ‎　‎ ‎5．（5分）（2012•湖南）已知双曲线C：的焦距为10，点P（2，1）在C的渐近线上，则C的方程为（　　）‎ A． B．‎ C． D．‎ ‎【分析】利用双曲线C：的焦距为10，点P（2，1）在C的渐近线上，建立方程组，求出a，b的值，即可求得双曲线的方程．‎ ‎【解答】解：∵双曲线C：的焦距为10，点P（2，1）在C的渐近线上，‎ ‎∴a2+b2=25，=1，‎ ‎∴b=，a=2‎ ‎∴双曲线的方程为．‎ 故选：A．‎ ‎　‎ ‎6．（5分）（2012•湖南）函数f（x）=sinx﹣cos（x+）的值域为（　　）‎ A．[﹣2，2] B．[﹣，] C．[﹣1，1] D．[﹣，]‎ ‎【分析】通过两角和的余弦函数化简函数的表达式，利用两角差的正弦函数化为一个角的一个三角函数的形式，求出函数的值域．‎ ‎【解答】解：函数f（x）=sinx﹣cos（x+）=sinx﹣+‎ ‎=﹣+‎ ‎=sin（x﹣）∈．‎ 故选B．‎ ‎　‎ ‎7．（5分）（2012•湖南）在△ABC中，AB=2，AC=3，•=1，则BC=（　　）‎ A． B． C．2 D．‎ ‎【分析】设∠B=θ，由•=1，利用平面向量的数量积运算法则列出关系式，表示出cosθ，再利用余弦定理表示出cosθ，两者相等列出关于BC的方程，求出方程的解即可得到BC的长．‎ ‎【解答】解：根据题意画出相应的图形，如图所示：‎ ‎∵•=1，设∠B=θ，AB=2，‎ ‎∴2•BC•cos（π﹣θ）=1，即cosθ=﹣，‎ 又根据余弦定理得：cosθ==，‎ ‎∴﹣=，即BC2=3，‎ 则BC=．‎ 故选A ‎　‎ ‎8．（5分）（2012•湖南）已知两条直线l1：y=m和l2：y=（m＞0），l1与函数y=|log2x|的图象从左至右相交于点A，B，l2与函数y=|log2x|的图象从左至右相交于点C，D．记线段AC和BD在X轴上的投影长度分别为a，b，当m变化时，的最小值为（　　）‎ A．16 B．8 C．8 D．4‎ ‎【分析】设A，B，C，D各点的横坐标分别为xA，xB，xC，xD ‎，依题意可求得为xA，xB，xC，xD的值，a=|xA﹣xC|，b=|xB﹣xD|，利用基本不等式可求得当m变化时，的最小值．‎ ‎【解答】解：设A，B，C，D各点的横坐标分别为xA，xB，xC，xD，‎ 则﹣log2xA=m，log2xB=m；﹣log2xC=，log2xD=；‎ ‎∴xA=2﹣m，xB=2m，xC=，xD=．‎ ‎∴a=|xA﹣xC|，b=|xB﹣xD|，‎ ‎∴==||=2m•=．‎ 又m＞0，∴m+=（2m+1）+﹣≥2﹣=（当且仅当m=时取“=”）‎ ‎∴≥=8．‎ 故选B．‎ ‎　‎ 二、填空题（共8小题，考生作答7小题，每小题0分，满分35分，9,10,11三题任选两题作答；12～16必做题）‎ ‎9．（2012•湖南）在直角坐标系xoy 中，已知曲线C1：（t为参数）与曲线C2：（θ为参数，a＞0 ）有一个公共点在X轴上，则a等于　　．‎ ‎【分析】化参数方程为普通方程，利用两曲线有一个公共点在x轴上，可得方程，即可求得结论．‎ ‎【解答】解：曲线C1：（t为参数）化为普通方程：2x+y﹣3=0，令y=0，可得x=‎ 曲线C2：（θ为参数，a＞0 ）化为普通方程：‎ ‎∵两曲线有一个公共点在x轴上，‎ ‎∴‎ ‎∴a=‎ 故答案为：‎ ‎　‎ ‎10．（5分）（2012•湖南）不等式|2x+1|﹣2|x﹣1|＞0的解集为　{x|x＞}　．‎ ‎【分析】由不等式|2x+1|﹣2|x﹣1|＞0⇔不等式|2x+1|＞2|x﹣1|⇔（2x+1）2＞4（x﹣1）2即可求得答案．‎ ‎【解答】解：∵|2x+1|﹣2|x﹣1|＞0，‎ ‎∴|2x+1|＞2|x﹣1|≥0，‎ ‎∴（2x+1）2＞4（x﹣1）2，‎ ‎∴x＞．‎ ‎∴不等式|2x+1|﹣2|x﹣1|＞0的解集为{x|x＞}．‎ 故答案为：{x|x＞}．‎ ‎　‎ ‎11．（5分）（2012•湖南）如图，过点P的直线与圆⊙O相交于A，B两点．若PA=1，AB=2，PO=3，则圆O的半径等于　　．‎ ‎【分析】设出圆的半径，根据切割线定理推出PA•PB=PC•PD，代入求出半径即可．‎ ‎【解答】解：设圆的半径为r，且 PO与圆交于C，D两点 ‎∵PAB、PCD是圆O的割线，‎ ‎∴PA•PB=PC•PD，‎ ‎∵PA=1，PB=PA+AB=3；‎ PC=3﹣r，PD=3+r，‎ ‎∴1×3=（3﹣r）×（3+r），‎ r2=6‎ ‎∴r=，‎ 故答案为：．‎ ‎　‎ ‎12．（5分）（2012•湖南）已知复数z=（3+i）2（i为虚数单位），则|z|=　10　．‎ ‎【分析】利用复数的模的平方等于复数的模的乘积，直接计算即可．‎ ‎【解答】解：复数z=（3+i）2（i为虚数单位），则|z|=|3+i||3+i|==10．‎ 故答案为：10．‎ ‎　‎ ‎13．（5分）（2012•湖南）（）6的二项展开式中的常数项为　﹣160　（用数字作答）．‎ ‎【分析】根据题意，利用二项展开式的通项公式求出展开式的通项，令x的指数为0，求出r，将r的值代入通项求出展开式的常数项．‎ ‎【解答】解：（）6展开式的通项为Tr+1=C6r•（2）6﹣r•（﹣）r=（﹣1）r•C6r•26﹣r•x3﹣r，‎ 令3﹣r=0，可得r=3，‎ 其常数项为T4=（﹣1）r•C6r•26﹣r=﹣160；‎ 故答案为﹣160．‎ ‎　‎ ‎14．（5分）（2012•湖南）如果执行如图所示的程序框图，输入x=﹣1，n=3，则输出的数S=　﹣4　．‎ ‎【分析】列出循环过程中S与K的数值，不满足判断框的条件即可结束循环．‎ ‎【解答】解：判断前x=﹣1，n=3，i=2，第1次判断后循环，S=﹣6+2+1=﹣3，i=1，‎ 第2次判断后S=5，i=0，‎ 第3次判断后S=﹣4，i=﹣1，‎ 第4次判断后﹣1≥0，不满足判断框的条件，结束循环，输出结果：﹣4．‎ 故答案为：﹣4．‎ ‎　‎ ‎15．（5分）（2012•湖南）函数f（x）=sin（ωx+φ）的导函数y=f′（x）的部分图象如图所示，其中，P为图象与y轴的交点，A，C为图象与x轴的两个交点，B为图象的最低点．‎ ‎（1）若φ=，点P的坐标为（0，），则ω=　3　；‎ ‎（2）若在曲线段与x轴所围成的区域内随机取一点，则该点在△ABC内的概率为　　．‎ ‎【分析】（1）先利用导数的运算性质，求函数f（x）的导函数f′（x），再将φ=，f′（0）=代入导函数解析式，即可解得ω的值；‎ ‎（2）先利用定积分的几何意义，求曲线段与x轴所围成的区域面积，再求三角形ABC的面积，最后利用几何概型概率计算公式求面积之比即可得所求概率．‎ ‎【解答】解：（1）∵函数f（x）=sin （ωx+φ）的导函数y=f′（x）=ωcos（ωx+φ），其中φ=，过点P（0，），‎ ‎∴ωcos=‎ ‎∴ω=3．‎ 故答案为：3．‎ ‎（2）∵f′（x）=ωcos（ωx+φ），‎ ‎∴曲线段与x轴所围成的区域面积为[﹣f′（x）]dx=﹣f（x）‎ ‎=﹣sin﹣（﹣sin）=2，‎ 三角形ABC的面积为=，‎ ‎∴在曲线段与x轴所围成的区域内随机取一点，则该点在△ABC内的概率为P==．‎ 故答案为：．‎ ‎　‎ ‎16．（5分）（2012•湖南）设N=2n（n∈N*，n≥2），将N个数x1，x2，…，xN依次放入编号为1，2，…，N的N个位置，得到排列P0=x1x2…xN．将该排列中分别位于奇数与偶数位置的数取出，并按原顺序依次放入对应的前和后个位置，得到排列P1=x1x3…xN﹣1x2x4…xN，将此操作称为C变换，将P1分成两段，每段个数，并对每段作C变换，得到P2，当2≤i≤n﹣2时，将Pi分成2i段，每段个数，并对每段作C变换，得到Pi+1，例如，当N=8时，P2=x1x5x3x7x2x6x4x8，此时x7位于P2中的第4个位置．‎ ‎（1）当N=16时，x7位于P2中的第　6　个位置；‎ ‎（2）当N=2n（n≥8）时，x173位于P4中的第　3×2n﹣4+11　个位置．‎ ‎【分析】（1）由题意，可按照C变换的定义把N=16时P2列举出，从中查出x7的位置即可；‎ ‎（2）根据C变换的定义及归纳（1）中的规律可得出P4中所有的数字分为16段，每段的数字序号组成以16为公差的等差数列，且一到十六段的首项的序号分别为1，3，5，7，9，11，13，15，2，4，6，8，10，12，14，16，再173=16×10+13，即可确定出x173位于P4中的位置．‎ ‎【解答】解：（1）当N=16时，P0=x1x2…x16．由C变换的定义可得P1=x1x3…x15x2x4…x16，‎ 又将P1分成两段，每段个数，并对每段作C变换，得到P2，故P2=x1x5x9x13x3x7x11x15x2x6x10x14x4x8x12x16，由此知x7位于P2中的第6个位置；‎ ‎（2）考察C变换的定义及（1）计算可发现，第一次C变换后，所有的数分为两段，每段的序号组成公差为2的等差数列，且第一段序号以1为首项，第二段序号以2为首项；第二次C变换后，所有的数据分为四段，每段的数字序号组成以4公差的等差数列，且第一段的序号以1为首项，第二段序号以3为首项，第三段序号以2为首项，第四段序号以4为首项，依此类推可得出P4中所有的数字分为16段，每段的数字序号组成以16为公差的等差数列，且一到十六段的首项的序号分别为1，9，5，13，…，由于173=16×10+13，故x173位于以13为首项的那一段的第11个数，由于N=2n（n≥8）故每段的数字有2n﹣4个，以13为首项的是第四段，故x173位于第3×2n﹣4+11=3×2n﹣4+11个位置．‎ 故答案为3×2n﹣4+11‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）（2012•湖南）某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示．‎ 一次性购物量 ‎1至4件 ‎5 至8件 ‎9至12件 ‎13至16件 ‎17件及以上 顾客数（人）‎ x ‎30‎ ‎25‎ y ‎10‎ 结算时间（分钟/人）‎ ‎1‎ ‎1.5‎ ‎2‎ ‎2.5‎ ‎3‎ 已知这100位顾客中的一次购物量超过8件的顾客占55%．‎ ‎（Ⅰ）确定x，y的值，并求顾客一次购物的结算时间X的分布列与数学期望；‎ ‎（Ⅱ）若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2.5分钟的概率．（注：将频率视为概率）‎ ‎【分析】（Ⅰ）由已知得25+y+10=55，x+30=45，故可确定，y的值，将频率视为概率，故可求相应的概率，由此可得X的分布列与数学期望；‎ ‎（Ⅱ）记A：一位顾客一次购物的结算时间不超过2.5分钟，Xi ‎（i=1，2）为该顾客前面第i位顾客的结算时间，则P（A）=P（（X1=1且X2=1）+P（（X1=1且X2=1.5）+P（（X1=1.5且X2=1），由于各顾客的结算相互独立，且Xi（i=1，2）的分布列都与X的分布列相同，故可得结论．‎ ‎【解答】解：（Ⅰ）由已知得25+y+10=55，x+30=45，所以x=15，y=20；‎ 将频率视为概率可得P（X=1）==0.15；P（X=1.5）==0.3；P（X=2）==0.25；P（X=2.5）==0.2；P（X=3）==0.1‎ X的分布列 ‎ X ‎ 1‎ ‎ 1.5‎ ‎ 2‎ ‎ 2.5‎ ‎ 3‎ ‎ P ‎ 0.15‎ ‎ 0.3‎ ‎ 0.25‎ ‎ 0.2‎ ‎ 0.1‎ X的数学期望为E（X）=1×0.15+1.5×0.3+2×0.25+2.5×0.2+3×0.1=1.9‎ ‎（Ⅱ）记A：一位顾客一次购物的结算时间不超过2.5分钟，Xi（i=1，2）为该顾客前面第i位顾客的结算时间，则 P（A）=P（（X1=1且X2=1）+P（（X1=1且X2=1.5）+P（（X1=1.5且X2=1）‎ 由于各顾客的结算相互独立，且Xi（i=1，2）的分布列都与X的分布列相同，所以 P（A）=0.15×0.15+0.15×0.3+0.3×0.15=0.1125‎ 故该顾客结算前的等候时间不超过2.5分钟的概率为0.1125．‎ ‎　‎ ‎18．（12分）（2012•湖南）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是CD的中点．‎ ‎（Ⅰ）证明：CD⊥平面PAE；‎ ‎（Ⅱ）若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P﹣ABCD的体积．‎ ‎【分析】解法一：（Ⅰ）先根据条件得到CD⊥AE；再结合PA⊥平面ABCD即可得到结论的证明；‎ ‎（Ⅱ）先根据直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等得到PA=BF，进而得到四边形BCDG是平行四边形，在下底面内求出BF的长以及下底面的面积，最后代入体积计算公式即可．‎ 法二：（Ⅰ）先建立空间直角坐标系，求出各点的坐标，进而得到=0以及•=0．即可证明结论；‎ ‎（Ⅱ）先根据直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等得到PA的长，再求出下底面面积，最后代入体积计算公式即可．‎ ‎【解答】解法一：（Ⅰ）连接AC，由AB=4，BC=3，∠ABC=90°，得AC=5，‎ 又AD=5，E是CD得中点，‎ 所以CD⊥AE，‎ PA⊥平面ABCD，CD⊂平面ABCD．‎ 所以PA⊥CD，‎ 而PA，AE是平面PAE内的两条相交直线，‎ 所以CD⊥平面PAE．‎ ‎（Ⅱ）过点B作BG∥CD，分别与AE，AD相交于点F，G，连接PF，‎ 由CD⊥平面PAE知，BG⊥平面PAE，于是∠BPF为直线PB与平面PAE所成的角，且BG⊥AE．‎ 由PA⊥平面ABCD知，∠PBA即为直线PB与平面ABCD所成的角．‎ 由题意∠PBA=∠BPF，因为sin∠PBA=，sin∠BPF=，所以PA=BF．‎ 由∠DAB=∠ABC=90°知，AD∥BC，又BG∥CD．‎ 所以四边形BCDG是平行四边形，‎ 故GD=BC=3，于是AG=2．‎ 在RT△BAG中，AB=4，AG=2，BG⊥AF，‎ 所以BG==2，BF===．‎ 于是PA=BF=．‎ 又梯形ABCD的面积为S=×（5+3）×4=16．‎ 所以四棱锥P﹣ABCD的体积为V=×S×PA=×16×=．‎ 解法二：以A为坐标原点，AB，AD，AP所在直线分别为X轴，Y轴，Z轴建立空间直角坐标系，‎ 设PA=h，则A（0，0，0），B（4，0，0），C（4，3，0），D（0，5，0），E（2，4，0），P（0，0，h）．‎ ‎（Ⅰ）=（﹣4，2，0），=（2，4，0），=（0，0，h）．‎ 因为=﹣8+8+0=0，•=0．‎ 所以CD⊥AE，CD⊥AP，而AP，AE是平面PAE内的两条相交直线，‎ 所以CD⊥平面PAE．‎ ‎（Ⅱ）由题设和第一问知，，分别是平面PAE，平面ABCD的法向量，‎ 而PB与平面PAE所成的角和PB与平面ABCD所成的角相等，‎ 所以：|cos＜，＞|=|cos＜，＞|，即||=||．‎ 由第一问知=（﹣4，2，0），=（（0，0，﹣h），又=（4，0，﹣h）．‎ 故||=||．‎ 解得h=．‎ 又梯形ABCD的面积为S=×（5+3）×4=16．‎ 所以四棱锥P﹣ABCD的体积为V=×S×PA=×16×=．‎ ‎　‎ ‎19．（12分）（2012•湖南）已知数列{an}的各项均为正数，记A（n）=a1+a2+…+an，B（n）=a2+a3+…+an+1，C（n）=a3+a4+…+an+2，n=1，2，…．‎ ‎（1）若a1=1，a2=5，且对任意n∈N*，三个数A（n），B（n），C（n）组成等差数列，求数列{an}的通项公式．‎ ‎（2）证明：数列{an}是公比为q的等比数列的充分必要条件是：对任意n∈N*，三个数A（n），B（n），C（n）组成公比为q的等比数列．‎ ‎【分析】（1）由于对任意n∈N*，三个数A（n），B（n），C（n）组成等差数列，可得到B（n）﹣A（n）=C（n）﹣B（n），即an+1﹣a1=an+2﹣a2，整理即可得数列{an}是首项为1，公差为4的等差数列，从而可得an．‎ ‎（2）必要性：由数列{an}是公比为q的等比数列，可证得即==q，即必要性成立；‎ 充分性：若对任意n∈N*‎ ‎，三个数A（n），B（n），C（n）组成公比为q的等比数列，可得an+2﹣qan+1=a2﹣qa1．由n=1时，B（1）=qA（1），即a2=qa1，从而an+2﹣qan+1=0，即充分性成立，于是结论得证．‎ ‎【解答】解：（1）∵对任意n∈N*，三个数A（n），B（n），C（n）组成等差数列，‎ ‎∴B（n）﹣A（n）=C（n）﹣B（n），‎ 即an+1﹣a1=an+2﹣a2，亦即an+2﹣an+1=a2﹣a1=4．‎ 故数列{an}是首项为1，公差为4的等差数列，于是an=1+（n﹣1）×4=4n﹣3．‎ ‎（2）证明：（必要性）：若数列{an}是公比为q的等比数列，对任意n∈N*，有an+1=anq．由an＞0知，A（n），B（n），C（n）均大于0，于是 ‎===q，‎ ‎===q，‎ 即==q，‎ ‎∴三个数A（n），B（n），C（n）组成公比为q的等比数列；‎ ‎（充分性）：若对任意n∈N*，三个数A（n），B（n），C（n）组成公比为q的等比数列，则 B（n）=qA（n），C（n）=qB（n），‎ 于是C（n）﹣B（n）=q[B（n）﹣A（n）]，即an+2﹣a2=q（an+1﹣a1），亦即an+2﹣qan+1=a2﹣qa1．‎ 由n=1时，B（1）=qA（1），即a2=qa1，从而an+2﹣qan+1=0．‎ ‎∵an＞0，‎ ‎∴==q．故数列{an}是首项为a1，公比为q的等比数列．‎ 综上所述，数列{an}是公比为q的等比数列的充分必要条件是：对任意n∈N*‎ ‎，三个数A（n），B（n），C（n）组成公比为q的等比数列．‎ ‎　‎ ‎20．（13分）（2012•湖南）某企业接到生产3000台某产品的A，B，C三种部件的订单，每台产品需要这三种部件的数量分别为2，2，1（单位：件）．已知每个工人每天可生产A部件6件，或B部件3件，或C部件2件．该企业计划安排200名工人分成三组分别生产这三种部件，生产B部件的人数与生产A部件的人数成正比，比例系数为K（K为正整数）．‎ ‎（1）设生产A部件的人数为x，分别写出完成A，B，C三种部件生产需要的时间；‎ ‎（2）假设这三种部件的生产同时开工，试确定正整数K的值，使完成订单任务的时间最短，并给出时间最短时具体的人数分组方案．‎ ‎【分析】（1）设完成A，B，C三种部件生产需要的时间分别为T1（x），T2（x），T3（x），则可得，，；‎ ‎（2）完成订单任务的时间为f（x）=max{T1（x），T2（x），T3（x）}，其定义域为，可得T1（x），T2（x）为减函数，T3（x）为增函数，T2（x）=T1（x），分类讨论：①当k=2时，T2（x）=T1（x），f（x）=max{T1（x），T3（x）}=max{}，利用基本不等式求出完成订单任务的最短时间；②当k≥3时，T2（x）＜T1（x），记，为增函数，φ（x）=max{T1（x），T（x）}f（x）=max{T1（x），T3（x）}≥max{T1（x），T（x）}=max{}，利用基本不等式求出完成订单任务的最短时间；③当k＜2时，k=1，f（x）=max{T2（x），T3（x）}=max{}，利用基本不等式求出完成订单任务的最短时间，从而问题得解．‎ ‎【解答】解：（1）设写出完成A，B，C三种部件生产需要的时间分别为T1（x），T2（x），T3（x）‎ ‎∴，，‎ 其中x，kx，200﹣（1+k）x均为1到200之间的正整数 ‎（2）完成订单任务的时间为f（x）=max{T1（x），T2（x），T3（x）}，其定义域为 ‎∴T1（x），T2（x）为减函数，T3（x）为增函数，T2（x）=T1（x）‎ ‎①当k=2时，T2（x）=T1（x），f（x）=max{T1（x），T3（x）}=max{}‎ ‎∵T1（x），T3（x）为增函数，∴当时，f（x）取得最小值，此时x=‎ ‎∵，，，f（44）＜f（45）‎ ‎∴x=44时，完成订单任务的时间最短，时间最短为 ‎②当k≥3时，T2（x）＜T1（x），‎ 记，为增函数，φ（x）=max{T1（x），T（x）}‎ f（x）=max{T1（x），T3（x）}≥max{T1（x），T（x）}=max{}‎ ‎∵T1（x）为减函数，T（x）为增函数，∴当时，φ（x）取得最小值，此时x=‎ ‎∵，，‎ ‎∴完成订单任务的时间大于 ‎③当k＜2时，k=1，f（x）=max{T2（x），T3（x）}=max{}‎ ‎∵T2（x）为减函数，T3（x）为增函数，∴当时，φ（x）取得最小值，此时x=‎ 类似①的讨论，此时完成订单任务的时间为，大于 综上所述，当k=2时，完成订单任务的时间最短，此时，生产A，B，C三种部件的人数分别为44，88，68．‎ ‎　‎ ‎21．（13分）（2012•湖南）在直角坐标系xoy中，曲线C1上的点均在C2：（x﹣5）2+y2=9外，且对C1上任意一点M，M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值．‎ ‎（Ⅰ）求曲线C1的方程 ‎（Ⅱ）设P（x0，y0）（y0≠±3）为圆C2外一点，过P作圆C2的两条切线，分别于曲线C1相交于点A，B和C，D．证明：当P在直线x=﹣4上运动时，四点A，B，C，D的纵坐标之积为定值．‎ ‎【分析】（Ⅰ）设M的坐标为（x，y），根据对C1上任意一点M，M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值，可得|x+2|=且圆C2上的点位于直线x=﹣2的右侧，从而可得曲线C1的方程；‎ ‎（Ⅱ）当点P在直线x=﹣4上运动时，P的坐标为（﹣4，y0），设切线方程为kx﹣y+y0+4k=0，利用直线与圆相切可得，从而可得过P所作的两条切线PA，PC的斜率k1，k2是方程的两个实根，设四点A，B，C，D的纵坐标分别为y1，y2，y3，y4，从而可得；同理可得，由此可得当P在直线x=﹣4上运动时，四点A，B，C，D的纵坐标之积为定值为6400．‎ ‎【解答】（Ⅰ）解：设M的坐标为（x，y），由已知得|x+2|=且圆C2上的点位于直线x=﹣2的右侧 ‎∴=x+5‎ 化简得曲线C1的方程为y2=20x ‎（Ⅱ）证明：当点P在直线x=﹣4上运动时，P的坐标为（﹣4，y0），‎ ‎∵y0≠±3，∴过P且与圆C2相切的直线的斜率k存在且不为0，每条切线都与抛物线有两个交点，切线方程为 y﹣y0=k（x+4），即kx﹣y+y0+4k=0，‎ ‎∴，整理得①‎ 设过P所作的两条切线PA，PC的斜率分别为k1，k2，则k1，k2是方程①的两个实根 ‎∴②‎ 由，消元可得③‎ 设四点A，B，C，D的纵坐标分别为y1，y2，y3，y4，‎ ‎∴y1，y2是方程③的两个实根 ‎∴④‎ 同理可得⑤‎ 由①②④⑤可得==6400‎ ‎∴当P在直线x=﹣4上运动时，四点A，B，C，D的纵坐标之积为定值为6400．‎ ‎　‎ ‎22．（13分）（2012•湖南）已知函数f（x）=eax﹣x，其中a≠0．‎ ‎（1）若对一切x∈R，f（x）≥1恒成立，求a的取值集合．‎ ‎（2）在函数f（x）的图象上取定两点A（x1，f（x1）），B（x2，f（x2）（x1＜x2），记直线AB的斜率为K，问：是否存在x0∈（x1，x2），使f′（x0）＞k成立？若存在，求x0的取值范围；若不存在，请说明理由．‎ ‎【分析】（1）先确定a＞0，再求导函数，确定函数的单调性，可得时，f（x）取最小值 故对一切x∈R，f（x）≥1恒成立，则，构建新函数g（t）=t﹣tlnt，则g′（t）=﹣lnt，确定函数的单调性，求出函数的最大值，由此即可求得a的取值集合；‎ ‎（2）由题意知，，构建新函数φ（x）=f′（x）﹣k=，则，，构建函数F（t）=et﹣t﹣1，从而可证明φ（x1）＜0，φ（x2）＞0，由此即可得到存在x0∈（x1，x2），使f′（x0）＞k成立．‎ ‎【解答】解：（1）若a＜0，则对一切x＞0，函数f（x）=eax﹣x＜1，这与题设矛盾，‎ ‎∵a≠0，∴a＞0‎ ‎∵f′（x）=aeax﹣1，令f′（x）=0，可得 令f′（x）＜0，可得，函数单调减；令f′（x）＞0，可得，函数单调增，‎ ‎∴时，f（x）取最小值 ‎∴对一切x∈R，f（x）≥1恒成立，则①‎ 令g（t）=t﹣tlnt，则g′（t）=﹣lnt 当0＜t＜1时，g′（t）＞0，g（t）单调递增；当t＞1时，g′（t）＜0，g（t）单调递减 ‎∴t=1时，g（t）取最大值g（1）=1‎ ‎∴当且仅当=1，即a=1时，①成立 综上所述，a的取值集合为{1}；‎ ‎（2）由题意知，‎ 令φ（x）=f′（x）﹣k=，则 令F（t）=et﹣t﹣1，则F′（t）=et﹣1‎ 当t＜0时，F′（t）＜0，函数单调减；当t＞0时，F′（t）＞0，函数单调增；‎ ‎∴t≠0时，F（t）＞F（0）=0，即et﹣t﹣1＞0‎ ‎∴，‎ ‎∵＞0，‎ ‎∴φ（x1）＜0，φ（x2）＞0‎ ‎∴存在c∈（x1，x2），φ（c）=0‎ ‎∵φ（x）单调递增，故这样的c是唯一的，且 当且仅当x∈（，x2）时，f′（x）＞k 综上所述，存在x0∈（x1，x2），使f′（x0）＞k成立，且x0的取值范围为（，x2）‎ ‎　‎ 参与本试卷答题和审题的老师有：qiss；吕静；xize；刘长柏；sllwyn；wfy814；庞会丽；danbo7801；xintrl（排名不分先后）‎ ‎2017年2月3日