2014高考湖南卷（文科数学）试卷

2014高考湖南卷（文科数学）试卷

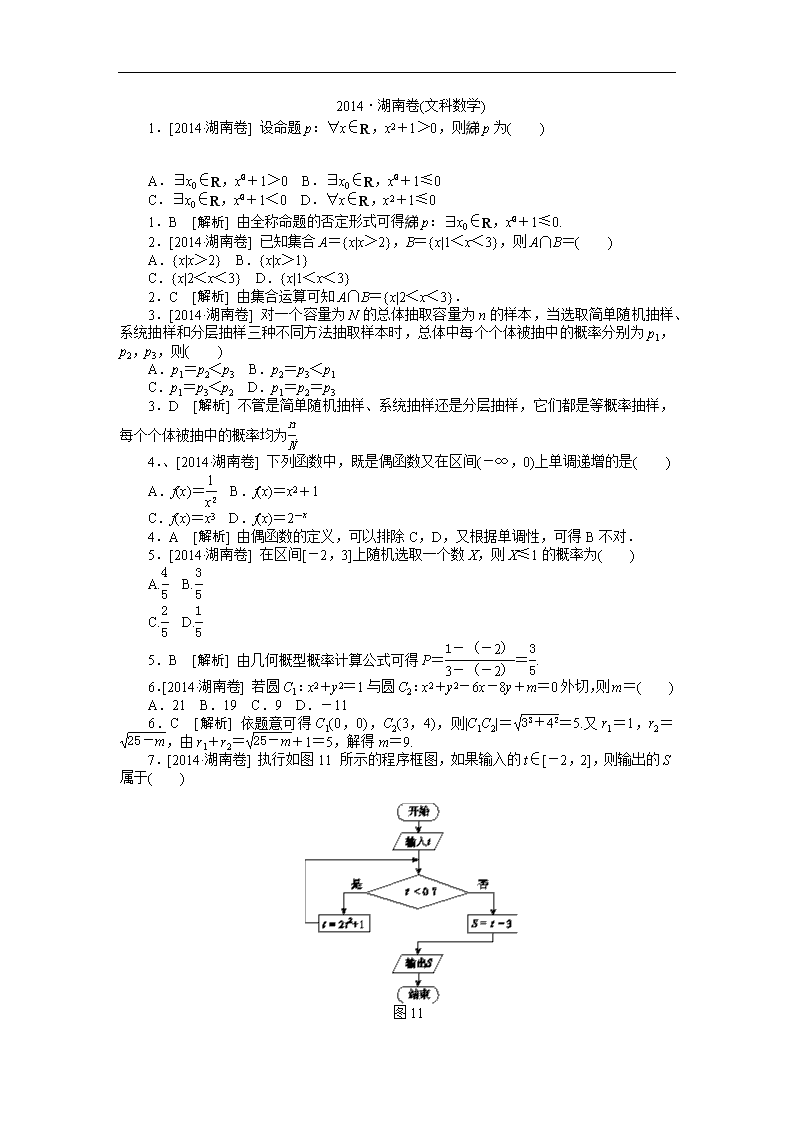
‎2014·湖南卷(文科数学)‎ ‎1．[2014·湖南卷] 设命题p：∀x∈R，x2＋1＞0，则綈p为(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A．∃x0∈R，x＋1＞0 B．∃x0∈R，x＋1≤0‎ C．∃x0∈R，x＋1＜0 D．∀x∈R，x2＋1≤0‎ ‎1．B　[解析] 由全称命题的否定形式可得綈p：∃x0∈R，x＋1≤0.‎ ‎2．[2014·湖南卷] 已知集合A＝{x|x＞2}，B＝{x|1＜x＜3}，则A∩B＝(　　)‎ A．{x|x＞2} B．{x|x＞1}‎ C．{x|2＜x＜3} D．{x|1＜x＜3}‎ ‎2．C　[解析] 由集合运算可知A∩B＝{x|2＜x＜3}．‎ ‎3．[2014·湖南卷] 对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为p1，p2，p3，则(　　)‎ A．p1＝p2＜p3 B．p2＝p3＜p1‎ C．p1＝p3＜p2 D．p1＝p2＝p3‎ ‎3．D　[解析] 不管是简单随机抽样、系统抽样还是分层抽样，它们都是等概率抽样，每个个体被抽中的概率均为. ‎ ‎4．、[2014·湖南卷] 下列函数中，既是偶函数又在区间(－∞，0)上单调递增的是(　　)‎ A．f(x)＝ B．f(x)＝x2＋1‎ C．f(x)＝x3 D．f(x)＝2－x ‎4．A　[解析] 由偶函数的定义，可以排除C，D，又根据单调性，可得B不对．‎ ‎5．[2014·湖南卷] 在区间[－2，3]上随机选取一个数X，则X≤1的概率为(　　)‎ A. B. C. D. ‎5．B　[解析] 由几何概型概率计算公式可得P＝＝.‎ ‎6．[2014·湖南卷] 若圆C1：x2＋y2＝1与圆C2：x2＋y2－6x－8y＋m＝0外切，则m＝(　　)‎ A．21 B．19 C．9 D．－11‎ ‎6．C　[解析] 依题意可得C1(0，0)，C2(3，4)，则|C1C2|＝＝5.又r1＝1，r2＝，由r1＋r2＝＋1＝5，解得m＝9.‎ ‎7．[2014·湖南卷] 执行如图11所示的程序框图，如果输入的t∈[－2，2]，则输出的S属于(　　)‎ 图11‎ A．[－6，－2] B．[－5，－1]‎ C．[－4，5] D．[－3，6]‎ ‎7．D　[解析] (特值法)当t＝－2时，t＝2×(－2)2＋1＝9，S＝9－3＝6，排除A，B，C.‎ ‎8．、[2014·湖南卷] 一块石材表示的几何体的三视图如图12所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于(　　)‎ 图12‎ A．1 B．2 C．3 D．4‎ ‎8．B　[解析] 由三视图可知，石材为一个三棱柱(相对应的长方体的一半)，故可知能得到的最大球为三棱柱的内切球．由题意可知正视图三角形的内切圆的半径即为球的半径，可得R＝＝2.‎ ‎9．[2014·湖南卷] 若0＜x1＜x2＜1，则(　　)‎ A．ex2－ex1＞ln x2－ln x1‎ B．ex2－ex1＜ln x2－ln x1‎ C．x2ex1＞x1ex2‎ D．x2ex1＜x1ex2‎ ‎9．C　[解析] 依题可构造函数f(x)＝，则f′(x)＝＝.当x∈(0，1)时，f′(x)＜0，所以f(x)＝在区间(0，1)上递减，故0＜x1＜x2＜1时有f(x1)＞f(x2)，即x2ex1＞x1ex2.‎ ‎10．[2014·湖南卷] 在平面直角坐标系中，O为原点，A(－1，0)，B(0，)，C(3，0)，动点D满足||＝1，则|＋＋|的取值范围是(　　)‎ A．[4，6] B．[－1，＋1]‎ C．[2，2] D．[－1，＋1]‎ ‎10．D　[解析] 由||＝1，得动点D在以点C为圆心，半径为1的圆上，故可设D(3＋cos α，sin α)，‎ 所以＋＋＝(2＋cos α，＋sin α)，所以|＋＋|2＝(2＋cos α)2＋(＋sin α)2＝8＋4cos α＋2sin α＝8＋2sin(α＋φ)，‎ 所以|＋＋|2∈[8－2，8＋2]，即|＋＋|∈[－1，＋1]．‎ ‎11．[2014·湖南卷] 复数(i为虚数单位)的实部等于________．‎ ‎11．－3　[解析] 因为＝＝－3－i，所以实部为－3.‎ ‎12．[2014·湖南卷] 在平面直角坐标系中，曲线C：(t为参数)的普通方程为 ‎________．‎ ‎12．x－y－1＝0　[解析] 依题意，消去参数可得x－2＝y－1，即x－y－1＝0.‎ ‎13．[2014·湖南卷] 若变量x，y满足约束条件则z＝2x＋y的最大值为________．‎ ‎13．7　[解析] 依题意，画出可行域，如图所示．‎ 由得点B的坐标为(3，1)，则z＝2x＋y在B(3，1)处取得最大值7.‎ ‎14．、[2014·湖南卷] 平面上一机器人在行进中始终保持与点F(1，0)的距离和到直线x＝－1的距离相等．若机器人接触不到过点P(－1，0)且斜率为k的直线，则k的取值范围是________．‎ ‎14．(－∞，－1)∪(1，＋∞)　[解析] 依题意可知机器人运行的轨迹方程为y2＝4x.设直线l：y＝k(x＋1)，联立消去y得k2x2＋(2k2－4)x＋k2＝0，由Δ＝(2k2－4)2－4k4＜0，得k2＞1，解得k＜－1或k＞1.‎ ‎15．[2014·湖南卷] 若f(x)＝ln(e3x＋1)＋ax是偶函数，则a＝________．‎ ‎15．－　[解析] 由偶函数的定义可得f(－x)＝f(x)，即ln(e－3x＋1)－ax＝ln(e3x＋1)＋ax，‎ ‎∴2ax＝－ln e3x＝－3x，∴a＝－.‎ ‎16．、[2014·湖南卷] 已知数列{an}的前n项和Sn＝，n∈N*.‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)设bn＝2an＋(－1)nan，求数列{bn}的前2n项和．‎ ‎ 16.解：(1)当n＝1时，a1＝S1＝1；‎ 当n≥2时，an＝Sn－Sn－1＝－＝n.‎ 故数列{an}的通项公式为an＝n.‎ ‎(2)由(1)知，bn＝2n＋(－1)nn.记数列{bn}的前2n项和为T2n，则T2n＝(21＋22＋…＋22n)＋(－1＋2－3＋4－…＋2n)．‎ 记A＝21＋22＋…＋22n，B＝－1＋2－3＋4－…＋2n，‎ 则A＝＝22n＋1－2，‎ B＝(－1＋2)＋(－3＋4)＋…＋[－(2n－1)＋2n]＝n.‎ 故数列{bn}的前2n项和T2n＝A＋B＝22n＋1＋n－2.‎ ‎17．、[2014·湖南卷] 某企业有甲、乙两个研发小组，为了比较他们的研发水平，现随机抽取这两个小组往年研发新产品的结果如下：‎ ‎(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)．‎ 其中a，a分别表示甲组研发成功和失败；b，b分别表示乙组研发成功和失败．‎ ‎(1)若某组成功研发一种新产品，则给该组记1分，否则记0分．试计算甲、乙两组研发新产品的成绩的平均数和方差，并比较甲、乙两组的研发水平．‎ ‎(2)若该企业安排甲、乙两组各自研发一种新产品，试估计恰有一组研发成功的概率．‎ ‎17．解：(1)甲组研发新产品的成绩为 ‎1，1，1，0，0，1，1，1，0，1，0，1，1，0，1，‎ 其平均数为x甲＝＝，‎ 方差为s＝＝.‎ 乙组研发新产品的成绩为 ‎1，0，1，1，0，1，1，0，1，0，0，1，0，1，1，‎ 其平均数为x乙＝＝，‎ 方差为s＝＝.‎ 因为x甲＞x乙，s＜s，所以甲组的研发水平优于乙组．‎ ‎(2)记E＝{恰有一组研发成功}．‎ 在所抽得的15个结果中，恰有一组研发成功的结果是(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，(a，b)，‎ 共7个，故事件E发生的频率为.‎ 将频率视为概率，即得所求概率为P(E)＝.‎ ‎18．、[2014·湖南卷] 如图13所示，已知二面角αMNβ的大小为60°，菱形ABCD在面β内，A，B两点在棱MN上，∠BAD＝60°，E是AB的中点，DO⊥面α，垂足为O.‎ 图13‎ ‎(1)证明：AB⊥平面ODE；‎ ‎(2)求异面直线BC与OD所成角的余弦值．‎ ‎18．解：(1)证明：如图，因为DO⊥α，AB⊂α，所以DO⊥AB.‎ 连接BD，由题设知，△ABD 是正三角形，又E是AB的中点，所以DE⊥AB.而DO∩DE＝D，故AB⊥平面ODE.‎ ‎(2)因为BC∥AD，所以BC与OD所成的角等于AD与OD所成的角，即∠ADO是BC与OD所成的角．‎ 由(1)知，AB⊥平面ODE，所以AB⊥OE.又DE⊥AB，于是∠DEO是二面角αMNβ的平面角，从而∠DEO＝60°.‎ 不妨设AB＝2，则AD＝2，易知DE＝.‎ 在Rt△DOE中，DO＝DE·sin 60°＝.‎ 连接AO，在Rt△AOD中，cos∠ADO＝＝‎ ＝.‎ 故异面直线BC与OD所成角的余弦值为.‎ ‎19．、、[2014·湖南卷] 如图14所示，在平面四边形ABCD中，DA⊥AB，DE＝1，EC＝，EA＝2，∠ADC＝，∠BEC＝.‎ ‎(1)求sin∠CED的值；‎ ‎(2)求BE的长．‎ 图14‎ ‎19．解：设∠CED＝α.‎ ‎(1)在△CDE中，由余弦定理，得 EC2＝CD2＋DE2－2CD·DE·cos∠EDC，‎ 于是由题设知，7＝CD2＋1＋CD，即CD2＋CD－‎ ‎6＝0，解得CD＝2(CD＝－3舍去)．‎ 在△CDE中，由正弦定理，得＝.‎ 于是，sin α＝＝＝，即 sin∠CED＝.‎ ‎(2)由题设知，0＜α＜，于是由(1)知，‎ cos α＝＝＝.‎ 而∠AEB＝－α，所以 cos∠AEB＝cos＝coscos α＋sinsin α ‎＝－cos α＋sin α ‎＝－×＋×＝.‎ 在Rt△EAB中，cos∠AEB＝＝，故 BE＝＝＝4.‎ ‎20．、、[2014·湖南卷] 如图15所示，O为坐标原点，双曲线C1：－＝1(a1＞0，b1＞0)和椭圆C2：＋＝1(a2＞b2＞0)均过点P，且以C1的两个顶点和C2的两个焦点为顶点的四边形是面积为2的正方形．‎ ‎(1)求C1，C2的方程．‎ ‎(2)是否存在直线l，使得l与C1交于A，B两点，与C2只有一个公共点，且|＋|＝|‎ AB| ？证明你的结论. ‎ 图15‎ ‎20．解： (1)设C2的焦距为2c2，由题意知，2c2＝2，2a1＝2，从而a1＝1，c2＝1.因为点P在双曲线x2－＝1上，所以－＝1，故b＝3.‎ 由椭圆的定义知 ‎2a2＝＋＝2.‎ 于是a2＝，b＝a－c＝2.故C1，C2的方程分别为x2－＝1，＋＝1.‎ ‎(2)不存在符合题设条件的直线．‎ ‎(i)若直线l垂直于x轴，因为l与C2只有一个公共点，所以直线l的方程为x＝或x＝－.‎ 当x＝时，易知A(，)，B(，－)，所以 ‎|＋|＝2，||＝2.‎ 此时，|＋|≠||.‎ 当 x＝－时，同理可知，|＋|≠||.‎ ‎(ii)若直线l不垂直于x轴，设l的方程为y＝kx＋m，‎ 由得(3－k2)x2－2kmx－m2－3＝0.‎ 当l与C1相交于A，B两点时，设A(x1，y1)，B(x2，y2)，则x1，x2是上述方程的两个实根，从而 x1＋x2＝，x1x2＝.‎ 于是y1y2＝k2x1x2＋km(x1＋x2)＋m2＝.‎ 由得(2k2＋3)x2＋4kmx＋2m2－6＝0.‎ 因为直线l与C2只有一个公共点，所以上述方程的判别式Δ＝16k2m2－8(2k2＋3)(m2－3)＝0.‎ 化简，得2k2＝m2－3.因此 ·＝x1x2＋y1y2＝＋＝≠0，‎ 于是2＋2＋2·≠2＋2－2·，即|＋|2≠|－|2.‎ 故|＋|≠||.‎ 综合(i)，(ii)可知，不存在符合题设条件的直线．‎ ‎21．、[2014·湖南卷] 已知函数f(x)＝xcos x－sin x＋1(x＞0)．‎ ‎(1)求f(x)的单调区间；‎ ‎(2)记xi为f(x)的从小到大的第i(i∈N*)个零点，证明：对一切n∈N*，有＋＋…＋＜.‎ ‎21．解： (1)f′(x)＝cos x－xsin x－cos x＝－xsin x.‎ 令f′(x)＝0，得x＝kπ(k∈N*)．‎ 当x∈(2kπ，(2k＋1)π)(k∈N)时，sin x>0，此时f′(x)<0; ‎ 当x∈((2k＋1)π，(2k＋2)π)(k∈N)时，sin x<0，此时f′(x)>0.‎ 故f(x)的单调递减区间为(2kπ，(2k＋1)π)(k∈N)，单调递增区间为((2k＋1)π，(2k＋2)π)(k∈N)．‎ ‎(2)由(1)知，f(x)在区间(0，π)上单调递减．又f＝0，故x1＝.‎ 当n∈N*时，因为 f(nπ)f＝[(－1)nnπ＋1][(－1)n＋1(n＋1)π＋1]＜0，‎ 且函数f(x)的图像是连续不断的，所以f(x)在区间(nπ，(n＋1)π)内至少存在一个零点．又f(x)在区间(nπ，(n＋1)π)上是单调的，故 nπ＜xn＋1＜(n＋1)π.‎ 因此，当n＝1时，＝＜；‎ 当n＝2时，＋＜(4＋1)＜；‎ 当n≥3时，‎ ＋＋…＋< ‎＜＜ ‎＝＜＜.‎ 综上所述，对一切n∈N*，＋＋…＋＜.‎