- 2021-04-18 发布 |
- 37.5 KB |
- 2页

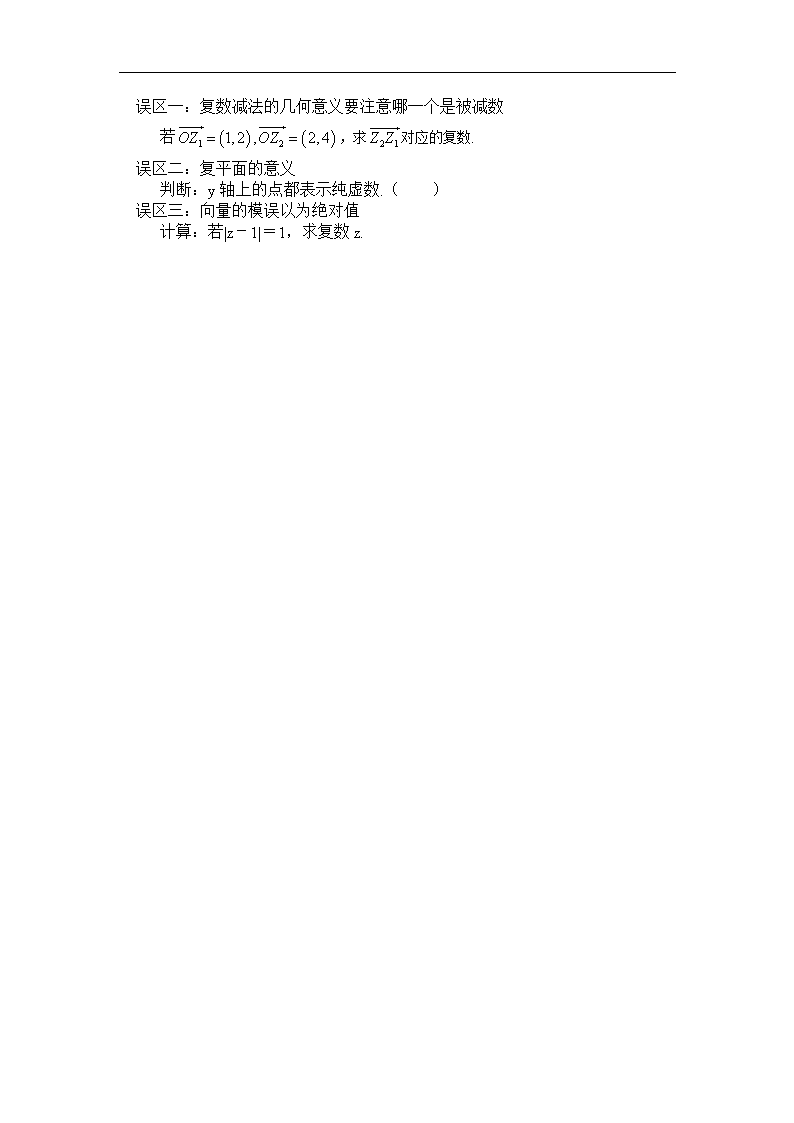
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习教案: 复数加、减法的几何意义备考策略
复数加、减法的几何意义备考策略 主标题:复数加、减法的几何意义备考策略 副标题:通过考点分析高考命题方向,把握高考规律,为学生备考复习打通快速通道。 关键词:复数加、减法,几何意义,备考策略 难度:3 重要程度:4 内容: 1、 复平面的定义,x轴,y轴的几何意义? 2、 复数与复平面内的点,向量如何建立一一对应的关系 3、 向量模的求法 思维规律解题 考点一:考查复数与复平面内点的对应关系 例1:(1)复数表示复平面内的点位于 A.第一象限B.第二象限C.第三象限D.第四象限 (2) 当实数m为何值时,, ①为纯虚数;②为实数;③对应的点在复平面内的第二象限内。 考点二:考查复数的模 例2:复数(i为虚数单位)的模是_________ 考点三:根据复数对应点所在的象限,求参数的取值范围 例3:在复平面内,复数对应的点分别为A、B,O为坐标原点,.若点P在第四象限内,则实数的取值范围是_____. 考点四:考查复数加减法的几何意义 例4:复平面内点A、B、C对应的复数分别为i、1、4+2i,由A→B→C→D按逆时针顺序作平行四边形ABCD,则=_____ 求复数模的方法: 一、定义法: 例5:若,求复数z的模. 二、 利用几何意义求模的取值范围 例6:若复数z满足|z-2|=1,求复数z的模的取值范围. 思维误区 误区一:复数减法的几何意义要注意哪一个是被减数 若,求对应的复数. 误区二:复平面的意义 判断:y轴上的点都表示纯虚数.( ) 误区三:向量的模误以为绝对值 计算:若|z-1|=1,求复数z.查看更多