- 2021-04-18 发布 |
- 37.5 KB |
- 8页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届高考数学一轮总复习课时作业39二元一次不等式组与简单的线性规划问题含解析苏教版
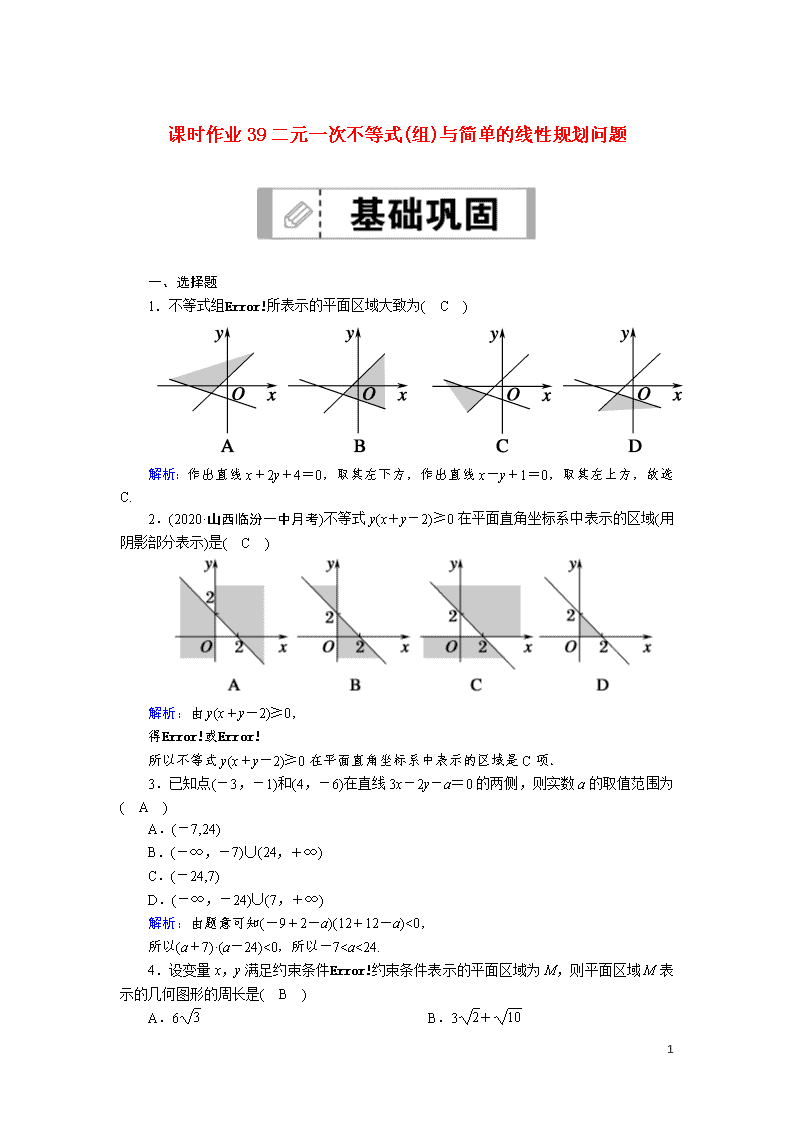
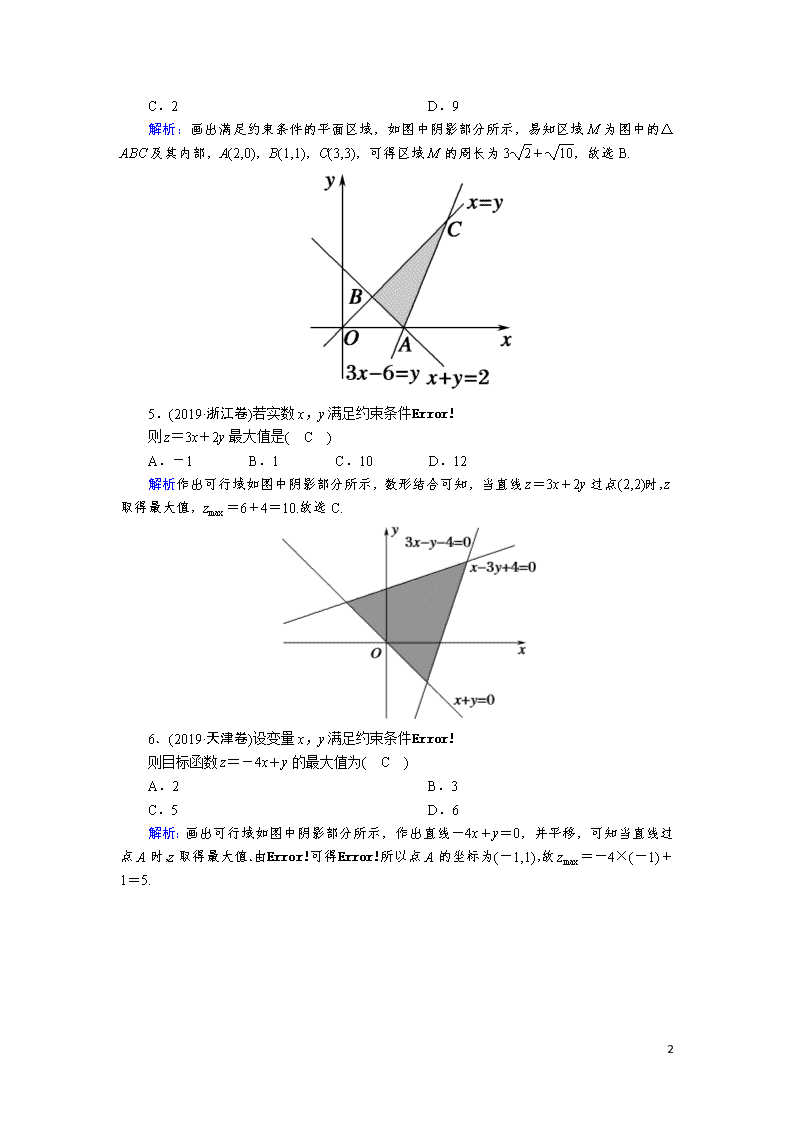
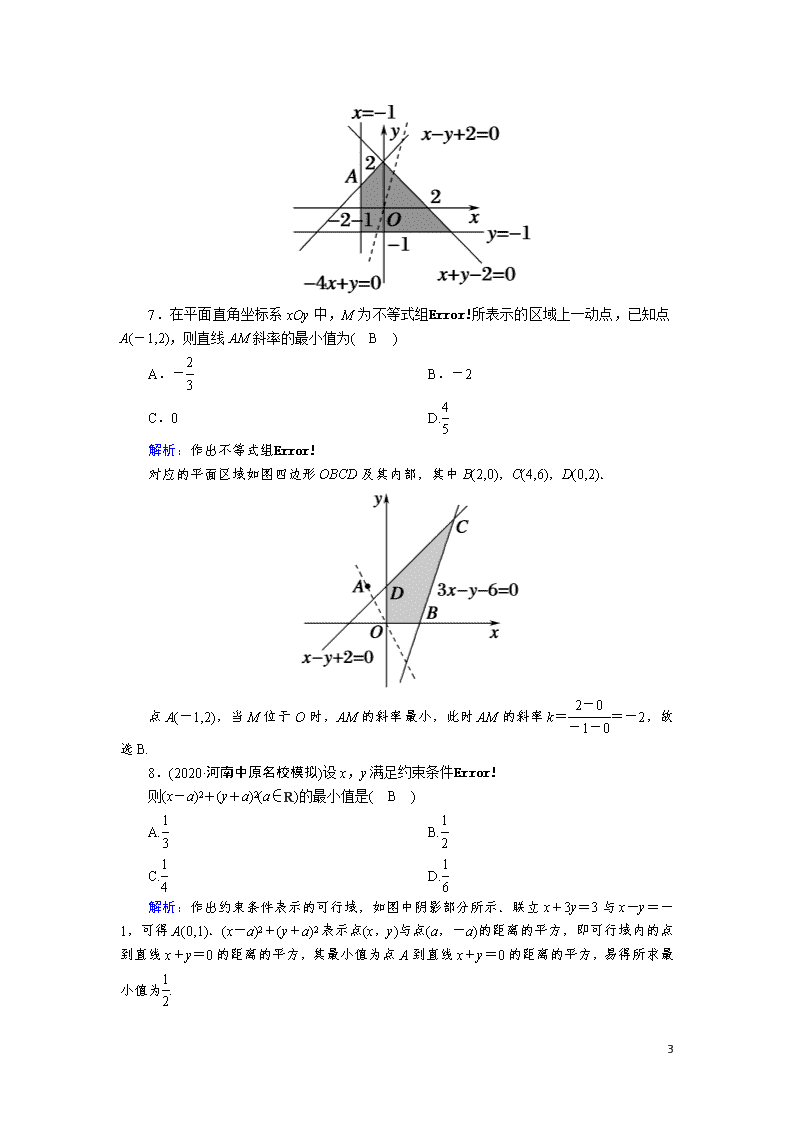
课时作业39二元一次不等式(组)与简单的线性规划问题 一、选择题 1.不等式组所表示的平面区域大致为( C ) 解析:作出直线x+2y+4=0,取其左下方,作出直线x-y+1=0,取其左上方,故选C. 2.(2020·山西临汾一中月考)不等式y(x+y-2)≥0在平面直角坐标系中表示的区域(用阴影部分表示)是( C ) 解析:由y(x+y-2)≥0, 得或 所以不等式y(x+y-2)≥0在平面直角坐标系中表示的区域是C项. 3.已知点(-3,-1)和(4,-6)在直线3x-2y-a=0的两侧,则实数a的取值范围为( A ) A.(-7,24) B.(-∞,-7)∪(24,+∞) C.(-24,7) D.(-∞,-24)∪(7,+∞) 解析:由题意可知(-9+2-a)(12+12-a)<0, 所以(a+7)·(a-24)<0,所以-7查看更多