- 2021-04-17 发布 |
- 37.5 KB |
- 31页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【新教材】2020-2021学年高中人教A版数学必修第二册课件:8-4-1 平面
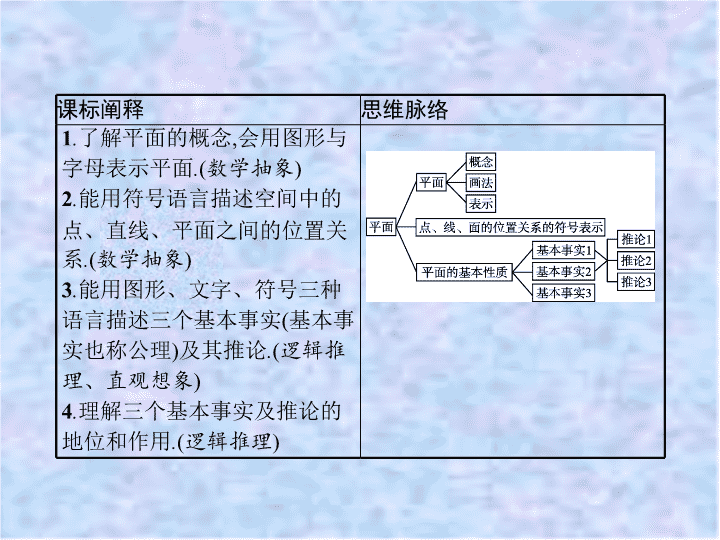
8 . 4 . 1 平面 课标阐释 思维脉络 1 . 了解平面的概念 , 会用图形与字母表示平面 . ( 数学抽象 ) 2 . 能用符号语言描述空间中的点、直线、平面之间的位置关系 . ( 数学抽象 ) 3 . 能用图形、文字、符号三种语言描述三个基本事实 ( 基本事实也称公理 ) 及其推论 . ( 逻辑推理、直观想象 ) 4 . 理解三个基本事实及推论的地位和作用 . ( 逻辑推理 ) 激趣诱思 知识点拨 在数学语言的研究中 , 通常按数学语言所使用的主要词汇 , 将数学语言分为三种 : 文字语言、符号语言、图形语言 . 例如 “ 点 A 在直线 l 上 ” 是利用文字来描述 , 以语言的形式表达出来的 , 因而称其为该定理的文字语言 ;“ A ∈ l ” 是用符号的形式将定理表达出来 , 因而称其为符号语言 ; 如果我们以图例或实物来表示定理的条件和结论 , 则称其为该定理的图形语言 . 通过文字语言以优美通畅的文字描述数学问题 , 言简意赅 , 寓意深刻 ; 通过符号语言表达数学问题 , 简明扼要 , 国际通行 ; 通过图形语言表达数学问题 , 形象生动 , 记忆深刻 . 几种语言各有特点 , 在学习立体几何时 , 应充分发挥不同语言的教育功能 . 激趣诱思 知识点拨 知识点一、 平面 平面的 描述性 概念 几何里所说的 “ 平面 ”, 就是从生活中一些物体中抽象出来的 . 平面是向四周 无限延展 的 画法 水平 放置 常把平行四边形的一边画成 横向 竖直 放置 常把平行四边形的一边画成 竖向 激趣诱思 知识点拨 记法 (1) 用希腊字母 α , β , γ 等表示平面 , 如平面 α 、平面 β 、平面 γ 等 , 并将它写在代表平面的平行四边形的一个角内 (2) 用代表平面的平行四边形的四个顶点的大写英文字母作为这个平面的名称 , 如平面 ABCD (3) 用代表平面的平行四边形的相对的两个顶点的大写英文字母作为这个平面的名称 , 如平面 AC, 平面 BD 名师点析 平面的概念可从以下三个方面理解 (1)“ 平面 ” 是平的 ;(2)“ 平面 ” 无厚度 ;(3)“ 平面 ” 可以向四周无限延展 . 激趣诱思 知识点拨 微练习 判断下列说法是否正确 , 并说明理由 . (1) 平面的形状是平行四边形 ; (2) 任何一个平面图形都是一个平面 ; (3) 两个平面相交的画法中 , 一个平面被另一个平面遮住时 , 被遮部分的线段应画成虚线或不画 ; (4) 三角形、圆、平行四边形都可以表示平面 . 解 : (1) 不正确 . 平面常用平行四边形表示 , 但不是平行四边形 , 平面是无限延展的 . (2) 不正确 . 平面图形与平面是两个不同的概念 , 平面图形具有大小、面积等属性 , 而平面则没有 , 平面是无限延展的 , 不可度量的 . (3) 正确 . 符合直观图画法的规则 . (4) 正确 . 三角形、圆、平行四边形都是平面图形 , 都可以表示平面 . 激趣诱思 知识点拨 知识点二、点、直线、平面之间的位置 关系 激趣诱思 知识点拨 知识点三、平面的基本性质 1 . 平面的基本性质 激趣诱思 知识点拨 激趣诱思 知识点拨 2 . 三个 推论 探究一 探究二 探究三 素养形成 当堂检测 证明点、线共面 例 1 证明 : 两两相交且不过同一点的三条直线共面 . 已知 : 如图所示 , l 1 ∩ l 2 =A , l 2 ∩ l 3 =B , l 1 ∩ l 3 =C. 求证 : 直线 l 1 , l 2 , l 3 在同一平面内 . 分析 先由 l 1 与 l 2 确定一个平面 , 再证明 l 3 在这个平面内 . 也可以证明 l 1 , l 2 确定的平面 α 与 l 2 , l 3 确定的平面 β 重合 . 探究一 探究二 探究三 素养形成 当堂检测 证明 : 方法一 ( 纳入平面法 ) ∵ l 1 ∩ l 2 =A , ∴ l 1 和 l 2 确定一个平面 α . ∵ l 2 ∩ l 3 =B , ∴ B ∈ l 2 . 又 l 2 ⊂ α , ∴ B ∈ α . 同理可证 C ∈ α . ∵ B ∈ l 3 , C ∈ l 3 , ∴ l 3 ⊂ α . ∴ 直线 l 1 , l 2 , l 3 在同一平面内 . 方法二 ( 辅助平面法 ) ∵ l 1 ∩ l 2 =A , ∴ l 1 , l 2 确定一个平面 α . ∵ l 2 ∩ l 3 =B , ∴ l 2 , l 3 确定一个平面 β . ∵ A ∈ l 2 , l 2 ⊂ α , ∴ A ∈ α . ∵ A ∈ l 2 , l 2 ⊂ β , ∴ A ∈ β . 同理可证 B ∈ α , B ∈ β , C ∈ α , C ∈ β . ∴ 不共线的三个点 A , B , C 既在平面 α 内 , 又在平面 β 内 . ∴ 平面 α 和 β 重合 , 即直线 l 1 , l 2 , l 3 在同一平面内 . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 证明点、线共面问题常用方法有 : (1) 先由部分点、线确定一个面 , 再证其余的点、线都在这个平面内 , 即用 “ 纳入平面法 ”; (2) 先由其中一部分点、线确定一个平面 α , 其余点、线确定另一个平面 β , 再证平面 α 与 β 重合 , 即用 “ 辅助平面法 ”; (3) 假设不共面 , 结合题设推出矛盾 , 用 “ 反证法 ” . 注意 : 在遇到文字叙述的结论时 , 一定要先根据题意画出图形 , 结合图形写出已知与求证 , 再证明 . 探究一 探究二 探究三 素养形成 当堂检测 延伸探究 (1) 如果把本例中的 “ 不过同一点 ” 删掉 , 那么这三条直线是否共面 ? (2) 如果把本例中 “ 三条直线 ” 改为 “ 四条直线 ”, 那么这四条直线是否共面 ? 试证明你的结论 . 解 : (1) 不一定共面 . ① 若三条直线两两相交 , 且过同一个点 . 这三条直线在同一个平面内相交 , 如图 . 这三条直线不共面 . 如图 . ② 若三条直线两两相交 , 且不过同一个点 , 由【例 1 】可知 , 这三条直线共面 . 探究一 探究二 探究三 素养形成 当堂检测 (2) 共面 . 已知 : a , b , c , d 四条直线两两相交 , 且不共点 . 求证 : a , b , c , d 四线共面 . 证明 : ① 无三线共点情况 , 如图 . 设 a ∩ d=M , b ∩ d=N , c ∩ d=P , a ∩ b=Q , a ∩ c=R , b ∩ c=S. 因为 a ∩ d=M , 所以 a , d 可确定一个平面 α . 因为 N ∈ d , Q ∈ a , 所以 N ∈ α , Q ∈ α , 所以 NQ ⊂ α , 即 b ⊂ α . 同理 , c ⊂ α , 所以 a , b , c , d 共面 . 探究一 探究二 探究三 素养形成 当堂检测 ② 有三线共点的情况 , 如图 . 设 b , c , d 三线相交于点 K , 与 a 分别交于 N , P , M 且 K ∉ a , 因为 K ∉ a , 所以 K 和 a 确定一个平面 , 设为 β . 因为 N ∈ a , a ⊂ β , 所以 N ∈ β . 所以 NK ⊂ β , 即 b ⊂ β . 同理 , c ⊂ β , d ⊂ β . 所以 a , b , c , d 共面 . 由 ①② 知 , a , b , c , d 共面 . 探究一 探究二 探究三 素养形成 当堂检测 证明点共线 例 2 已知 △ ABC 在平面 α 外 , AB ∩ α =P , AC ∩ α =R , BC ∩ α =Q , 如图 . 求证 : P , Q , R 三点共线 . 分析 证明 P , Q , R 三点既在平面 ABC 内 , 也在平面 α 内 , 即得 P , Q , R 共线 . 也可以证明点 Q 既在平面 APR 内 , 也在平面 α 内 , 即点 Q 在平面 APR 与平面 α 的交线 PR 上 . 探究一 探究二 探究三 素养形成 当堂检测 证明 : ( 方法一 ) ∵ AB ∩ α =P , ∴ P ∈ AB , P ∈ 平面 α . 又 AB ⊂ 平面 ABC , ∴ P ∈ 平面 ABC. ∴ 由基本事实 3 可知点 P 在平面 ABC 与平面 α 的交线上 , 同理可证 Q , R 也在平面 ABC 与平面 α 的交线上 , ∴ P , Q , R 三点共线 . ( 方法二 ) ∵ AP ∩ AR=A , ∴ 直线 AP 与直线 AR 确定平面 APR. 又 AB ∩ α =P , AC ∩ α =R , ∴ 平面 APR ∩ 平面 α =PR. ∵ B ∈ 平面 APR , C ∈ 平面 APR , ∴ BC ⊂ 平面 APR. ∵ Q ∈ BC , ∴ Q ∈ 平面 APR. 又 Q ∈ α , ∴ Q ∈ PR , ∴ P , Q , R 三点共线 . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 点共线 : 证明多点共线通常利用基本事实 3, 即两相交平面交线的唯一性 , 通过证明点分别在两个平面内 , 证明点在相交平面的交线上 ; 也可先选择其中两点确定一条直线 , 再证明其他点也在其上 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 1 如图所示 , 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , 设 A 1 C ∩ 平面 ABC 1 D 1 =E. 则 B , E , D 1 三点的 关系为 . ( 填 “ 共线 ” 或 “ 不共线 ”) 解析 : 如图所示 , 连接 A 1 B , BD 1 , CD 1 . ∵ A 1 C ∩ 平面 ABC 1 D 1 =E , ∴ E ∈ A 1 C , E ∈ 平面 ABC 1 D 1 . ∵ A 1 C ⊂ 平面 A 1 BCD 1 , ∴ E ∈ 平面 A 1 BCD 1 . ∵ 平面 A 1 BCD 1 ∩ 平面 ABC 1 D 1 =BD 1 , ∴ E ∈ BD 1 , ∴ B , E , D 1 三点共线 . 答案 : 共线 探究一 探究二 探究三 素养形成 当堂检测 证明线共点 例 3 如图所示 , 三个平面 α , β , γ 两两相交于不同的直线 , 即 α ∩ β =c , β ∩ γ =a , γ ∩ α =b , 若直线 a 和 b 不平行 , 求证 : a , b , c 三条直线必过同一点 . 分析 由 a , b 都在平面 γ 内且不平行 , 得 a , b 相交 , 再证明交点在 c 上 , 即证明交点在以 c 为交线的两个平面 α , β 内 . 探究一 探究二 探究三 素养形成 当堂检测 证明 : ∵ α ∩ γ =b , β ∩ γ =a , ∴ a ⊂ γ , b ⊂ γ . ∵ 直线 a 和 b 不平行 , ∴ a , b 必相交 . 如图所示 , 设 a ∩ b=P , 则 P ∈ a , P ∈ b. ∵ a ⊂ β , b ⊂ α , ∴ P ∈ β , P ∈ α . 又 α ∩ β =c , ∴ P ∈ c , 即交线 c 经过点 P. ∴ a , b , c 三条直线必过同一点 . 反思感悟 证明三线共点常用的方法是先说明两条直线共面且相交于一点 , 再说明这个点在以另一条直线为交线的两个平面内 , 即该点在另一条直线上 , 则可得三线共点 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 2 如图所示 , 在空间四边形 ABCD 中 , E , F 分别是 AB 和 CB 上的点 , G , H 分别是 CD 和 AD 上的点 , HG ∥ EF , HG ∶ EF= 1 ∶ 3 . 求证 : EH , BD , FG 三条直线相交于同一点 . 证明 : 延长 EH , FG , 不妨设 EH ∩ FG=O , ∵ HG ∥ EF , HG ∶ EF= 1 ∶ 3, 且 EF ≠ GH , ∴ 四边形 EFGH 为梯形 , ∴ EH , FG 共面 , 且 EH 与 FG 不平行 . ∵ O ∈ EH , EH ⊂ 平面 ABD , ∴ O ∈ 平面 ABD , ∵ O ∈ FG , FG ⊂ 平面 BCD , ∴ O ∈ 平面 BCD. ∵ 平面 ABD ∩ 平面 BCD=BD , ∴ O ∈ BD , ∴ EH , BD , FG 三条直线相交于同一点 O. 探究一 探究二 探究三 素养形成 当堂检测 转化思想在文字语言、图形语言与符号语言中的应用 典例 (1) 用符号语言表示下列语句 , 并画出图形 . ① 三个平面 α , β , γ 相交于一点 P , 且平面 α 与平面 β 相交于 PA , 平面 α 与平面 γ 相交于 PB , 平面 β 与平面 γ 相交于 PC ; ② 平面 ABD 与平面 BDC 相交于 BD , 平面 ABC 与平面 ADC 相交于 AC. (2) 用文字语言和符号语言表示下图 . 分析 (1) 根据条件 , 先适当确定其中的某一个平面 , 再根据点、线、面的位置关系 , 将其附着于固定平面上 , 注意图形的立体感 , 要将被遮挡部分用虚线表示 . (2) 用文字语言、符号语言表示一个图形时 , 应仔细观察图形有几个平面、几条直线且相互之间的位置关系如何 . 探究一 探究二 探究三 素养形成 当堂检测 解 : (1) ① 符号语言 : α ∩ β ∩ γ =P , α ∩ β =PA , α ∩ γ =PB , β ∩ γ =PC ; 图形表示如图 ① 所示 . ② 符号语言 : 平面 ABD ∩ 平面 BDC=BD , 平面 ABC ∩ 平面 ADC=AC ; 图形表示如图 ② 所示 . ① ② (2) 文字语言 : 平面 α 内的直线 m 和 n 相交于点 A. 符号语言 : m ⊂ α , n ⊂ α , 且 m ∩ n=A. 探究一 探究二 探究三 素养形成 当堂检测 方法点睛 用文字语言、符号语言表示一个图形时 , 首先仔细观察图形 , 有几个平面且位置关系如何 , 有几条直线且位置关系如何 , 图中的直线和平面的位置关系如何 , 有几点且在哪条直线或哪个平面上等 , 试着用文字语言表示 , 然后用符号语言表示 . 根据符号语言或文字语言画相应的图形时 , 要注意实线和虚线的区别 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 下列四个选项中的图形表示两个相交平面 , 其中画法正确的是 ( ) 解析 : 选项 A 错误 , 理由是两平面的交线没画出 , 且被遮挡的部分未用虚线画出 ; 选项 B,C 都错误 , 理由是被遮挡的部分未用虚线画出 . D 正确 . 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 1 . 经过空间任意三点作平面 ( ) A . 只有一个 B . 可作两个 C . 可作无数多个 D . 只有一个或有无数多个 解析 : 当三点在一条直线上时 , 过这三点能作无数个平面 ; 当三点不在同一条直线上时 , 过这三点的平面有且只有一个 . 故选 D . 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 2 . 下列图形中 , 不一定是平面图形的是 ( ) A . 三角形 B . 平行四边形 C . 梯形 D . 四边相等的四边形 解析 : 利用基本事实 1 可知 : 三角形、平行四边形、梯形一定是平面图形 , 而四边相等的四边形不一定是平面图形 . 故选 D . 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 3 . 下列说法正确的是 ( ) A. 镜面是一个平面 B. 一个平面长 10 m, 宽 5 m C. 一个平面的面积是另一个平面面积的 2 倍 D. 所有的平面都是无限延展的 解析 : 镜面可以抽象成平面 , 但不是平面 , 所以选项 A 不正确 ; 平面没有大小 , 所以选项 B 和选项 C 都不正确 , 故选 D . 答案 : D 4 . 已知平面 α ∩ 平面 β =l , 点 P ∈ α , P ∈ β , 则点 P 与直线 l 的关系是 . 答案 : P ∈ l 探究一 探究二 探究三 素养形成 当堂检测 5 . 不重合的三条直线 , 若相交于一点 , 最多能确定 个平面 . 解析 : 三条直线相交于一点 , 最多可确定 3 个平面 , 如图所示 , 直线 a , b , c 相交于点 A , 直线 a , b 确定平面 α , 直线 b , c 确定平面 β , 直线 a , c 确定平面 γ , 共 3 个平面 . 答案 : 3查看更多