- 2021-04-17 发布 |
- 37.5 KB |
- 34页


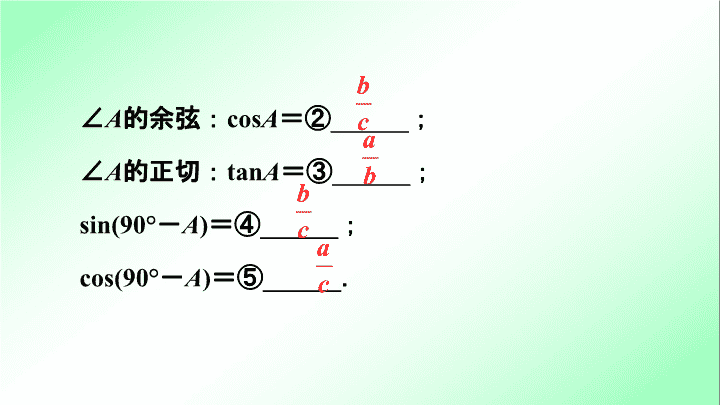
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学中考总复习课件PPT:第21课时 锐角三角函数及其应用
第一部分 夯实基础 提分多 第 四 单元 三角形 第 21 课时 锐角三角函数及其应用 1 . 三角函数的概念 如图 (1) ,在 Rt△ ABC 中,∠ C = 90 ° ,∠ A 为△ ABC 中的一锐角,则有∠ A 的正弦: sin A =① ______ ; 基础点 1 锐角三角函数 图 (1) 基础点巧练妙记 ∠ A 的余弦: cos A =② ______ ; ∠ A 的正切: tan A =③ ______ ; sin(90 ° - A ) =④ ______ ; cos(90 ° - A ) =⑤ ______ . 30 ° 45 ° 60 ° sinα ⑥_____ cosα ⑦____ tanα ⑧_____ 角度 α 三角 函数值 1 2 . 特殊角的三角函数值 基础点 2 直角三角形的边角关系 已知条件 解法步骤 两直角边 ( a , b ) 斜边 c ,直角边 a 解法 类型 已知条件 计算边的口诀: 有斜求对乘正弦; 有斜求邻乘余弦; 无斜求对乘正切; 无斜求邻除正切 锐角∠ A , 锐角∠ A 的邻边 b 锐角∠ A , 锐角∠ A 的对边 a 解法 类型 解法步骤 已知条件 计算边的口诀: 有斜求对乘正弦; 有斜求邻乘余弦; 无斜求对乘正切; 无斜求邻除正切 斜边 c ,锐角 ∠A 解法 类型 解法步骤 有斜用弦 ( 条件或求解中有斜边时,用正弦 sin 或余弦 cos) 无斜用切 ( 条件或求解中没有斜边时,用正切 tan) 取原避中 ( 尽量用原始数据,避免中间近似,否则会增大最后答案的误差 ) 宁乘勿除 ( 能用乘法的尽量用乘法,可以提高计算的准确度 ) 练 提 分 必 1 .如图,在 Rt△ABC 中,∠ ACB = 90 ° , D 是 AB 的中点, CD = 2 cm ,则 AB = ________cm. 2 .已知 Rt△ABC 的斜边长为 6 cm ,则斜边上的中线长为 ________cm. 第 1 题图 4 3 基础点 3 解直角三角形的实际应用 图 (3) 仰角、俯角 坡度(坡比)、坡脚 图 (4) 方向角 图 (5) 【 温馨提示 】 精确度:一个数四舍五入到哪一位就说这个数精确到那一位,如 0.3125 精确到 0.1 为 0.3 ,精确到百分位为 0.31. 重难点精讲优练 类型 解直角三角形的实际应用 例题图 例题图 例题图 (2) 求 A 、 B 两点间的距离; 例题图 例题图 (3) 现在要在道路 EH 段建造一家大型超市 P ,使得超市到 B 的距离最短,求超市 P 应建造在距离河岸边 H 多远的地方? ( 参考数据: sin53 ° ≈45 , tan53 ° ≈43) 例题图 【 思维教练 】 作 BP ⊥ AE ,由△ ABP ∽△ AEB ,求得 AP ,由△ AHF ∽△ AED 求得 AH ,可得 HP = AP - AH ,即可求解. 例题解图 例题解图 例题解图 练习 1 题图 100 练习 2 题图 练习 2 (2017 邵阳 ) 如图所示,运载火箭从地面 L 处垂直向上发射,当火箭到达 A 点时,从位于地面 R 处的雷达测得 AR 的距离是 40 km ,仰角是 30 ° . n 秒后,火箭到达 B 点,此时仰角是 45 ° ,则火箭在这 n 秒中上升的高度是 ________km. 练习 2 题图 练习 3 题图 练习 2 如图,轮船在 A 处观测灯塔 C 位于北偏西 70 ° 方向上,轮船从 A 处以每小时 20 海里的速度沿南偏西 50 ° 方向匀速航行, 1 小时后到达码头 B 处,此时,观测灯塔 C 位于北偏西 25 ° 方向上,求灯塔 C 与码头 B 的距离. 解 :如解图,作 BD ⊥ AC 于点 D , ∠ CBA = 25° + 50° = 75° , ∠ CAB = (90° - 70°) + (90° - 50°) = 20° + 40° = 60° , ∴∠ ABD = 90° -∠ CAB = 90° - 60° = 30° , 练习 3 题解图 练习 3 题解图 练习 3 题解图 导 方 法 指 常用的方法有两类: 类型 1 三角形做高法: 图形 关系式 AB = AD - BD 导 方 法 指 图形 关系式 AB = AD - BD 导 方 法 指 图形 关系式 BC = BD + CD 导 方 法 指 类型 2 梯形做高法 图形 关系式 AC = AE - CE 导 方 法 指 图形 关系式 AB = BE + AE = CD + AE 导 方 法 指 图形 关系式 BC = BE + EF + FC查看更多