- 2021-02-26 发布 |
- 37.5 KB |
- 31页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版六级下册数学数学广角鸽巢问题例例
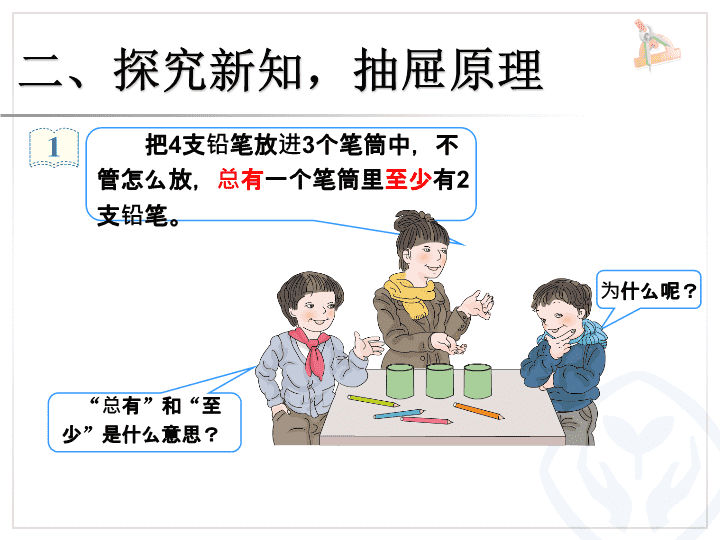
一、游戏引入,导入新知 我给大家表演一个 “ 魔术 ” 。一副牌, 取出大小王 ,还剩 52 张,你们 5 人 每人随意抽一张,我知道至少有 2 张牌是同花色的。相信吗? 二、探究新知,抽屉原理 把 4 支铅笔放进 3 个笔筒中,不管怎么放, 总有 一个笔筒里 至少 有 2 支铅笔。 为什么呢? “ 总有 ” 和 “ 至少 ” 是什么意思? “ 总有 ” 就是说 “ 一定有一个笔筒 ”。 “ 至少 ” 就是说 “ 不少于 2 支,可能是 2 支,也可能多于 2 支 ” 。 把 4 支铅笔放进 3 个笔筒里,总有一个笔筒里 至少放 2 支铅笔,为什么? 抽屉原理 一 小组讨论,看哪一组最先得出结论? 我把情况记录下来。 0 我把情况记录下来。 不管怎么放 , 总有一个笔筒里至少放进 2 支铅笔。 把 4 支铅笔放进 3 个笔筒中。 只要物体比抽屉数目多 1 个,总有一个抽屉里至少放进 2 个物体。 还可以这么想,如果每个笔筒只放 1 支铅笔 , 最多放 3 支。剩下的 1 支还要放进其中的一个笔筒。所以至少有 2 支铅笔放进同一个笔筒。 我把各种情况都摆出来了。 还可以这样想:先放 3 支, 在每个笔筒中放 1 支 , 剩下 的 1 支就要放进其中的一个笔筒。所以至少有一个笔筒中有 2 支铅笔。 抽屉原理 一 抽屉原理一 只要放的 物体 比 抽屉 的数量 多 1 ,总有一个抽屉里 至少 放入 2 个 物体。 把 7 本 书放进 3 个 抽屉,不管怎么放,总有一个抽屉里至少放进 3 本书。为什么? 我随便放放看, 一个抽屉 1 本, 一个抽屉 2 本, 一个抽屉 4 本。 如果每个抽屉最多放 2 本,那么 3 个抽屉最多放 6 本,可题目要求放的是 7 本书。所以 …… 两种放法都有一个抽屉 放了 3 本 或 多于 3 本,所以 …… 抽屉原理 二 不管怎么放 , 总有一个抽屉里 至少放进 3 本书 . 抽屉原理 二 0 0 0 0 摆一摆: 0 通过摆一摆我们可以得出 7 本书放在 3 个抽屉中,有 8 种情况,总有一个抽屉里至少有 3 本书。 枚举法: 7 7 0 0 7 6 1 0 7 5 2 0 7 5 1 1 7 4 3 0 7 4 2 1 7 3 3 3 7 3 2 2 把 7 本书放进 3 个抽屉中,也就是把 7 分解成 3 个数,有 8 种情况,总有一个抽屉里至少有 3 本书。 把 7 本书平均分成 3 份, 7÷3=2 …… 1 ,如果每个抽屉放 2 本,还剩 1 本,把剩下的这 1 本书放进任何 1 个抽屉,该抽屉里就有 3 本书了。 假设法: 7 本书放进 3 个抽屉,总有一个抽屉至少放进 3 本书。 如果把 8 本书放进 3 个抽屉里呢 ? 10 本书放进 3 个抽屉呢 ? 8÷3=2 …… 2 ,把 8 本书放进 3 个抽屉,总有 1 个抽屉至少放进 3 本书。 10÷3=3 …… 1 ,把 10 本书放进 3 个抽屉,总有 1 个抽屉至少放进 4 本书。 7 ÷ 3 = 2 …… 1 8 ÷ 3 = 2 …… 2 10 ÷ 3 = 3 …… 1 7 本书放进 3 个抽屉,有一个抽屉至少放 3 本书。 8 本书 …… 你是这样想的吗?你有什么发现? 抽屉原理 二 物体数 ÷ 抽屉数 = 商 …… 余数 至少数: 商 + 1 如果物体数 除以 抽屉数 有余数 , 用所得的 商加 1 , 就会发现: “ 总有一个抽屉里至少有 商加 1 个物体”。 我发现 …… 抽屉原理 二 抽屉原理二 把 a 个物体放进 n 个抽屉里,如果 a÷n=b …… c ( C 不等于零且 C查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档