- 2021-04-17 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年山东省东营市中考数学试卷【含答案;word版本试题;可编辑】
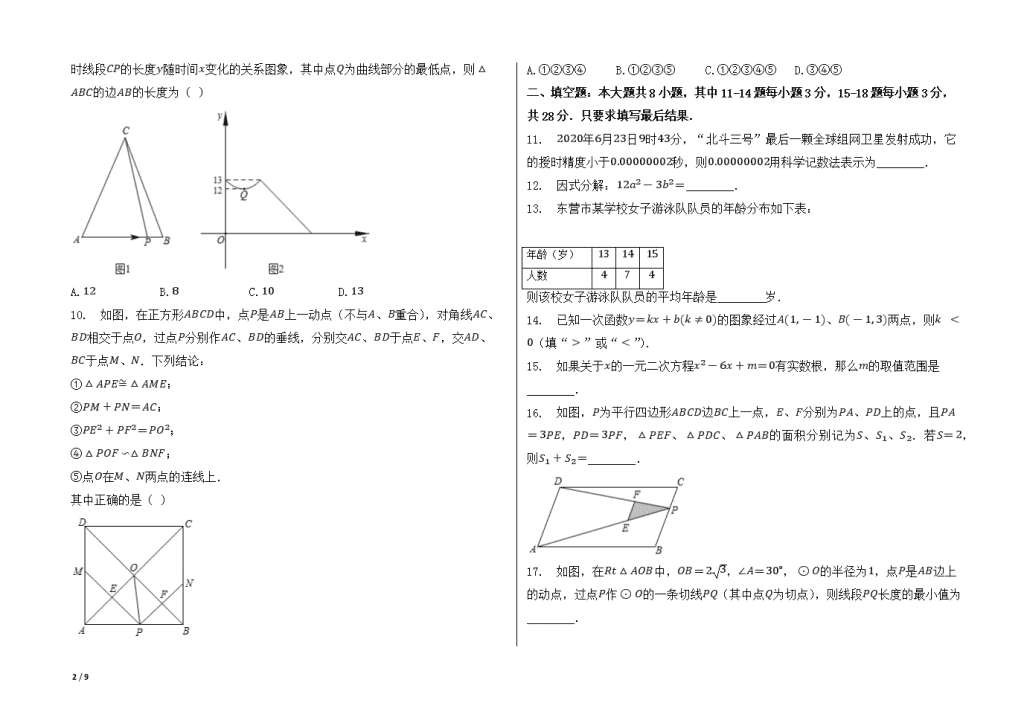
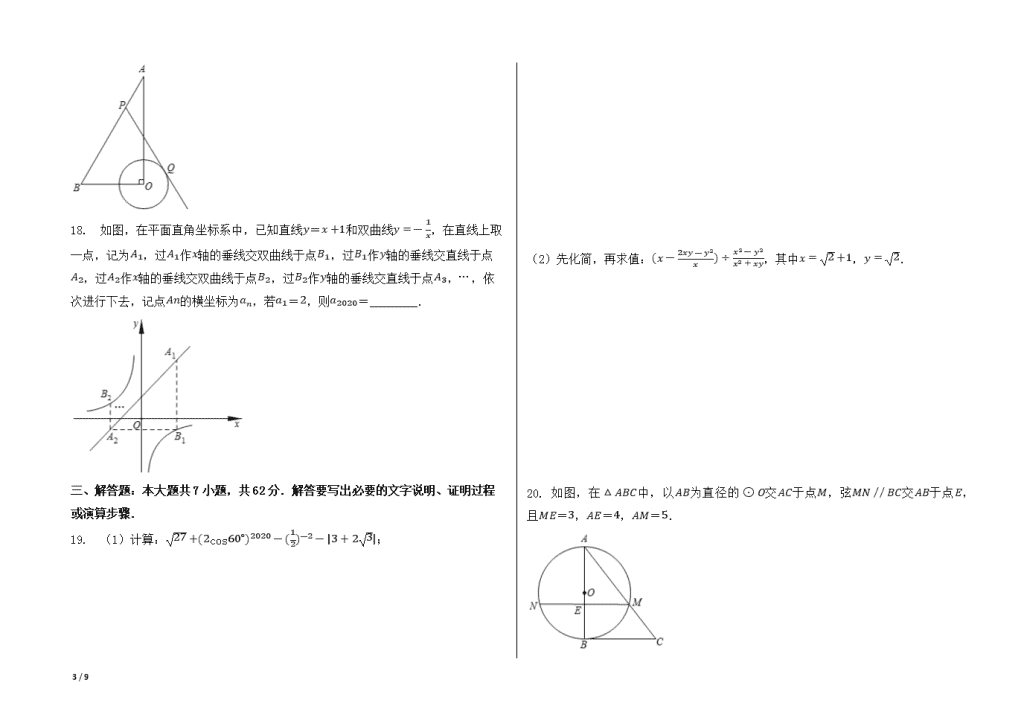
2020年山东省东营市中考数学试卷 一、选择题:本大题共10题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分. 1. -6的倒数是( ) A.-6 B.6 C.-16 D.16 2. 下列运算正确的是( ) A.(x3)2=x5 B.(x-y)2=x2+y2 C.-x2y3⋅2xy2=-2x3y5 D.-(3x+y)=-3x+y 3. 利用科学计算器求值时,小明的按键顺序为,则计算器面板显示的结果为( ) A.-2 B.2 C.±2 D.4 4. 如图,直线AB、CD相交于点O,射线OM平分∠BOD,若∠AOC=42∘,则∠AOM等于( ) A.159∘ B.161∘ C.169∘ D.138∘ 5. 如图.随机闭合开关K1、K2、K3中的两个,则能让两盏灯泡L1、L2同时发光的概率为( ) A.16 B.12 C.23 D.13 6. 如图,已知抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,其对称轴与x轴交于点C,其中A、C两点的横坐标分别为-1和1,下列说法错误的是( ) A.abc<0 B.4a+c=0 C.16a+4b+c<0 D.当x>2时,y随x的增大而减小 7. 用一个半径为3,面积为3π的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( ) A.π B.2π C.2 D.1 8. 中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去某关口,路程378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.则此人第三天走的路程为( ) A.96里 B.48里 C.24里 D.12里 9. 如图1,点P从△ABC的顶点A出发,沿A→B→C匀速运动到点C,图2是点P运动时线段CP 9 / 9 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则△ABC的边AB的长度为( ) A.12 B.8 C.10 D.13 10. 如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论: ①△APE≅△AME; ②PM+PN=AC; ③PE2+PF2=PO2; ④△POF∽△BNF; ⑤点O在M、N两点的连线上. 其中正确的是( ) A.①②③④ B.①②③⑤ C.①②③④⑤ D.③④⑤ 二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果. 11. 2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于0.00000002秒,则0.00000002用科学记数法表示为________. 12. 因式分解:12a2-3b2=________. 13. 东营市某学校女子游泳队队员的年龄分布如下表: 年龄(岁) 13 14 15 人数 4 7 4 则该校女子游泳队队员的平均年龄是________岁. 14. 已知一次函数y=kx+b(k≠0)的图象经过A(1, -1)、B(-1, 3)两点,则k < 0(填“>”或“<”). 15. 如果关于x的一元二次方程x2-6x+m=0有实数根,那么m的取值范围是________. 16. 如图,P为平行四边形ABCD边BC上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为S、S1、S2.若S=2,则S1+S2=________. 17. 如图,在Rt△AOB中,OB=23,∠A=30∘,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为________. 9 / 9 18. 如图,在平面直角坐标系中,已知直线y=x+1和双曲线y=-1x,在直线上取一点,记为A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交直线于点A2,过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交直线于点A3,…,依次进行下去,记点An的横坐标为an,若a1=2,则a2020=________. 三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤. 19. (1)计算:27+(2cos60∘)2020-(12)-2-|3+23|; (2)先化简,再求值:(x-2xy-y2x)÷x2-y2x2+xy,其中x=2+1,y=2. 20. 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN // BC交AB于点E,且ME=3,AE=4,AM=5. 9 / 9 (1)求证:BC是⊙O的切线; (2)求⊙O的直径AB的长度. 21. 如图,C处是一钻井平台,位于东营港口A的北偏东60∘方向上,与港口A相距602海里,一艘摩托艇从A出发,自西向东航行至B时,改变航向以每小时50海里的速度沿BC方向行进,此时C位于B的北偏西45∘方向,则从B到达C需要多少小时? 22. 东营市某中学对2020年4月份线上教学学生的作业情况进行了一次抽样调查,根据收集的数据绘制了如图不完整的统计图表. 作业情况 频数 频率 非常好 44 0.22 较好 68 0.34 一般 48 0.24 不好 40 0.20 请根据图表中提供的信息,解答下列问题: (1)本次抽样共调查了多少名学生? (2)将统计表中所缺的数据填在表中横线上; (3)若该中学有1800名学生,估计该校学生作业情况“非常好”和“较好”的学生一共约多少名? (4)某学习小组4名学生的作业本中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些作业本封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本中再抽取一本,请用“列表法”或“画树状图”的方法求出两次抽到的作业本都是“非常好”的概率. 9 / 9 23. 2020年初,XXXXX爆发,市场上防XX口罩热销,某医药公司每月生产甲、乙两种型号的防XX口罩共20万只,且所有口罩当月全部售出,其中成本、售价如下表: 型号 价格(元/只) 项目 甲 乙 成本 12 4 售价 18 6 (1)若该公司三月份的销售收入为300万元,求生产甲、乙两种型号的防XX口罩分别是多少万只? (2)如果公司四月份投入成本不超过216万元,应怎样安排甲、乙两种型号防XX口罩的产量,可使该月公司所获利润最大?并求出最大利润. 24. 如图,抛物线y=ax2-3ax-4a的图象经过点C(0, 2),交x轴于点A、B(点A在点B左侧),连接BC,直线y=kx+1(k>0)与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F. (1)求抛物线的解析式及点A、B的坐标; (2)EFDF是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由. 9 / 9 25. 如图1,在等腰三角形ABC中,∠A=120∘,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点. (1)观察猜想. 图1中,线段NM、NP的数量关系是________,∠MNP的大小为________. (2)探究证明 把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP、BD、CE,判断△MNP的形状,并说明理由; (3)拓展延伸 把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请求出△MNP面积的最大值. 9 / 9 参考答案与试题解析 2020年山东省东营市中考数学试卷 一、选择题:本大题共10题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分. 1.C 2.C 3.B 4.A 5.6.B 7.D 8.B 9.C 10.B 二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果. 11.2×10-8 12.3(2a+b)(2a-b) 13.14 14.< 15.m≤9 16.18 17.22 18.2 三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤. 19.原式=33+(2×12)2020-22-(3+23) =33+1-4-3-23 =3-6; 原式=x2-2xy+y2x⋅x2+xyx2-y2 =(x-y)2x⋅x(x+y)(x+y)(x-y) =x-y. 当x=2+1,y=2时, 原式=2+1-2 =1. 20.证明:∵ 在△AME中,ME=3,AE=4,AM=5, ∴ AM2=ME2+AE2, ∴ △AME是直角三角形, ∴ ∠AEM=90∘, 又∵ MN // BC, ∴ ∠ABC=∠AEM=90∘, ∴ AB⊥BC, ∵ AB为直径, ∴ BC是⊙O的切线; 连接OM,如图,设⊙O的半径是r, 在Rt△OEM中,OE=AE-OA=4-r,ME=3,OM=r, ∵ OM2=ME2+OE2, ∴ r2=32+(4-r)2, 9 / 9 解得:r=258, ∴ AB=2r=254. 21.过C作CD⊥AB于D,在点A的正北方向上取点M,在点B的正北方向上取点N, 由题意得:∠MAB=∠NBA=90∘,∠MAC=60∘,∠NBC=45∘,AC=602海里, ∴ ∠CDA=∠CDB=90∘, ∵ 在Rt△ACD中,∠CAD=∠MAB-∠MAC=90∘-60∘=30∘, ∴ CD=12AC=302(海里), 在Rt△BCD中,∠CDB=90∘,∠CBD=∠NBD-∠NBC=90∘-45∘=45∘, ∴ BC=2CD=60(海里), ∴ 60÷50=1.2(小时), ∴ 从B处到达C岛处需要1.2小时. 22.根据题意得:40÷72360=200(名), 则本次抽样共调查了200名学生; 填表如下: 作业情况 频数 频率 非常好 44 0.22 较好 68 0.34 一般 48 0.24 不好 40 0.20 故答案为:44;48;0.34;0.24;0.20; 根据题意得:1800×(0.22+0.34)=1008(名), 则该校学生作业情况“非常好”和“较好”的学生一共约1008名; 列表如下: A1 A2 B C A1 --- (A1, A2) (A1, B) (A1, C) A2 (A2, A1) --- (A2, B) (A2, C) B (B, A1) (B, A2) --- (B, C) C (C, A1) (C, A2) (C, B) --- 由列表可以看出,一共有12种结果,且它们出现的可能性相等,其中两次抽到的作业本都是“非常好”的有2种, 则P(两次抽到的作业本都是“非常好”)=212=16. 23.生产甲、乙两种型号的防XX口罩分别是15万只和5万只; 安排生产甲种型号的防XX口罩17万只,乙种型号的防XX口罩3万只,最大利润为108万元 24.把C(0, 2)代入y=ax2-3ax-4a得:-4a=2. 解得a=-12. 则该抛物线解析式为y=-12x2+32x+2. 9 / 9 由于y=-12x2+32x+2=-12(x+1)(x-4). 故A(-1, 0),B(4, 0); 存在,理由如下: 由题意知,点E位于y轴右侧,作EG // y轴,交BC于点G, ∴ CD // EG, ∴ EFDF=EGCD. ∵ 直线y=kx+1(k>0)与y轴交于点D,则D(0, 1). ∴ CD=2-1=1. ∴ EFDF=EG. 设BC所在直线的解析式为y=mx+n(m≠0). 将B(4, 0),C(0, 2)代入,得4m+n=0n=2 . 解得m=-12n=2 . ∴ 直线BC的解析式是y=-12x+2. 设E(t, -12t2+32t+2),则G(t, -12t+2),其中0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档