- 2021-04-17 发布 |
- 37.5 KB |
- 74页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学试题汇编之25 相似试题及答案
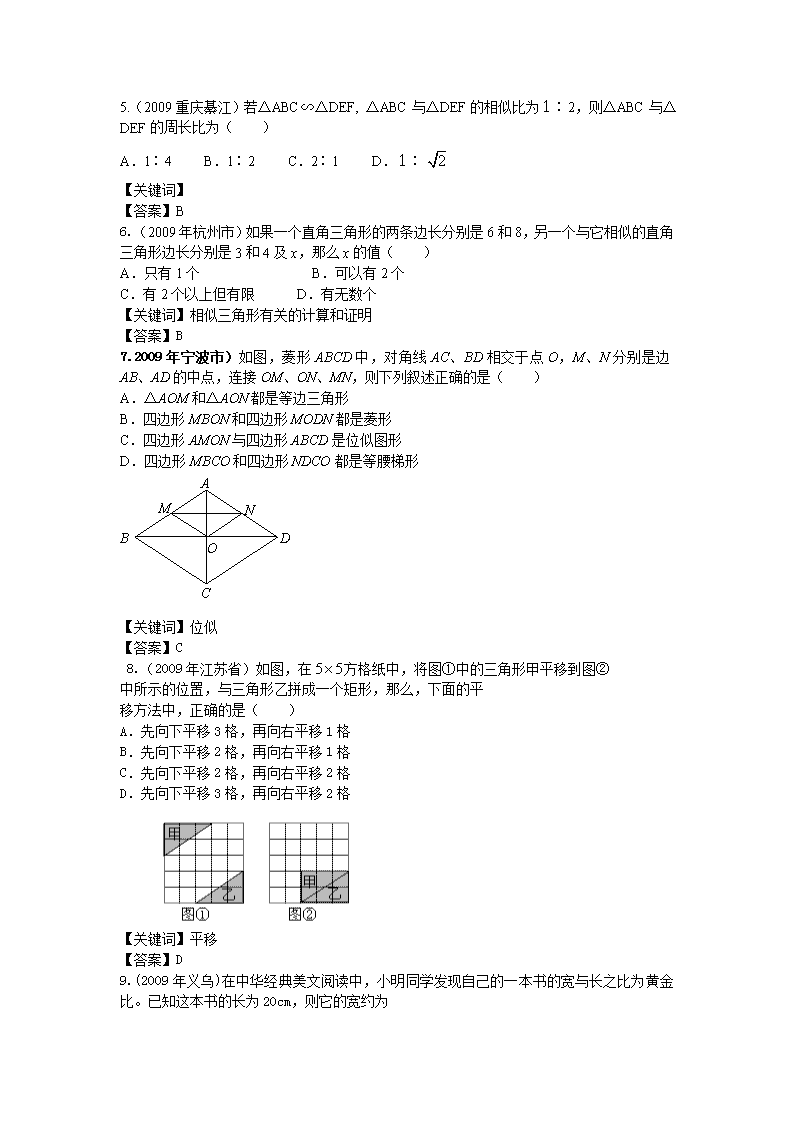
2009年中考试题专题之25-相似试题及答案 一、选择题 1.(2009年滨州)如图所示,给出下列条件: ①;②;③;④. 其中单独能够判定的个数为( ) A.1 B.2 C.3 D.4 【关键词】三角形相似的判定. 【答案】C 2.(2009年上海市)如图,已知,那么下列结论正确的是( ) A. B. C. D. 【关键词】平行线分线段成比例 【答案】A 3.(2009成都)已知△ABC∽△DEF,且AB:DE=1:2,则△ABC的面积与△DEF的面积之比为 (A)1:2 (B)1:4 (C)2:1 (D)4:1 【关键词】 【答案】B 4. (2009年安顺)如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论: (1)DE=1,(2)△CDE∽△CAB,(3)△CDE的面积与△CAB的面积之比为1:4.其中正确的有: A.0个 B.1个 C.2个 D.3个 【关键词】等边三角形,三角形中位线,相似三角形 【答案】D 5.(2009重庆綦江)若△ABC∽△DEF, △ABC与△DEF的相似比为1∶2,则△ABC与△DEF的周长比为( ) A.1∶4 B.1∶2 C.2∶1 D.1∶ 【关键词】 【答案】B 6.(2009年杭州市)如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( ) A.只有1个 B.可以有2个 C.有2个以上但有限 D.有无数个 【关键词】相似三角形有关的计算和证明 【答案】B 7.2009年宁波市)如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是( ) A.△AOM和△AON都是等边三角形 B.四边形MBON和四边形MODN都是菱形 C.四边形AMON与四边形ABCD是位似图形 D.四边形MBCO和四边形NDCO都是等腰梯形 D B C A N M O 【关键词】位似 【答案】C 8.(2009年江苏省)如图,在方格纸中,将图①中的三角形甲平移到图② 中所示的位置,与三角形乙拼成一个矩形,那么,下面的平 移方法中,正确的是( ) A.先向下平移3格,再向右平移1格 B.先向下平移2格,再向右平移1格 C.先向下平移2格,再向右平移2格 D.先向下平移3格,再向右平移2格 【关键词】平移 【答案】D 9.(2009年义乌)在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比。已知这本书的长为20cm,则它的宽约为 A.12.36cm B.13.6cm C.32.36cm D.7.64cm 【关键词】黄金比 【答案】A 10. (2009年娄底)小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图4所示,在射击时,小明有轻微的抖动,致使准星A偏离到A′,若OA=0.2米,OB=40米,AA′=0.0015米,则小明射击到的点B′偏离目标点B的长度BB′为 ( ) A.3米B.0.3米C.0.03米D.0.2米 【关键词】相似三角形 【答案】B 11.(2009恩施市)如图,在中,是上一点,于,且,则的长为( ) A.2 B. C. D. 【关键词】解直角三角形、相似 【答案】B 12.(2009年甘肃白银)如图3,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为( ) A.12m B.10m C.8m D.7m 【关键词】相似三角形判定和性质 【答案】A 13.(2009年孝感)如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1,则B′点的坐标为 A. B. C. D. 【关键词】旋转 【答案】A 14.(2009年孝感)美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为 A.4cm B.6cm C.8cm D.10cm 【关键词】黄金比 【答案】C 15. (2009年新疆)如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是( ) A. 【关键词】相似三角形的判定 【答案】A 16.(2009年天津市)在和中,,如果的周长是16,面积是12,那么的周长、面积依次为( ) A.8,3 B.8,6 C.4,3 D.4,6 【关键词】相似三角形的性质 【答案】A 17.(2009年牡丹江市)如图, 中,于一定能确定为直角三角形的条件的个数是( ) ①②③④ ⑤ A.1 B.2 C.3 D.4 【关键词】三角形相似的判定和性质 【答案】C 18. (2009白银市)如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为( ) A.12m B.10m C.8m D.7m 【关键词】相似三角形的判定和性质 【答案】A 19. (2009年衢州)在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为 A.9.5 B.10.5 C.11 D.15.5 【关键词】线段的比和比例线段 【答案】D 20.(2009年衢州)如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是 A. B. C. D. 【关键词】相似三角形判定和性质 【答案】D 21.(2009年舟山)在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为 A.9.5 B.10.5 C.11 D.15.5 【关键词】线段的比和比例线段 【答案】D 22.(2009年舟山)如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是 A. B. C. D. 【关键词】相似三角形判定和性质 【答案】D 23.(2009年济宁市)如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( ) A. 2 cm2 B. 4 cm2 C. 8 cm2 D. 16 cm2 【关键词】相似多边形 【答案】C 24. (2009年福州)如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( ) A.2DE=3MN, B.3DE=2MN, C. 3∠A=2∠F D.2∠A=3∠F 【关键词】位似变换 【答案】B 25.(2009年宜宾)若一个图形的面积为2,那么将它与成中心对称的图形放大为原来的两倍后的图形面积为( ) A. 8 B. 6 C. 4 D. 2 【关键词】相似图形的性质 【答案】A. 26. .(2009年广西梧州)如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于( ) A. B. C. D. 【关键词】相似三角形 【答案】D 27.(2009年甘肃定西)如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为( ) A.12m B.10m C.8m D.7m 【关键词】相似三角形 【答案】A 28. (2009年湖州)如图,在正三角形中,,,分别是,,上的点,,,,则的面积与的面积之比等于( ) A.1∶3 B.2∶3 C.∶2 D.∶3 【关键词】等边三角形的性质,相似的性质 【答案】A 29.(2009年温州)一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( ) A.第4张 B.第5张 C.第6张 D.第7张 【关键词】等腰三角形性质,三角形相似的性质,梯形中位线 【答案】C 30.(2009年兰州)如图,丁轩同学在晚上由路灯走向路灯,当他走到点时,发现身后他影子的顶部刚好接触到路灯的底部,当他向前再步行20m到达点时,发现身前他影子的顶部刚好接触到路灯的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是 A.24m B.25m C.28m D.30m 【关键词】相似三角形、灯光与影子 【答案】D 31.(2009年济宁市)如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( ) A. 2 cm2 B. 4 cm2 C. 8 cm2 D. 16 cm2 【关键词】相似多边形 【答案】C 32. (09湖南怀化)如图1,、分别是、的中点,则( ) A. 1∶2 B.1∶3 C.1∶4 D. 2∶3 【关键词】相似三角形有关的计算 【答案】C 33. (2009年山西省)如图,是的直径,是的切线,点在上,,则的长为( ) A. B. C. D. 【关键词】圆周角和圆心角;切线定理;相似三角形有关的计算;相似三角形与圆 【答案】A 34.(2009年山西省)如图,在中,的垂直平分线交的延长线于点,则的长为( ) A. B. C. D.2 【关键词】相似三角形判定和性质;勾股定理;线段和角的概念、性质 【答案】B 35. (2009年枣庄市)如图,△DEF是由△ABC经过位似变换得到的, 点O是位似中心,D,E,F分别是OA,OB,OC 的中点,则△DEF与△ABC的面积比是( ) A. B. C. D. 【关键词】相似三角形有关的计算和证明 【答案】B 36. (2009呼和浩特)如图,AB是的直径,点C在圆上,,则图中与相似的三角形的个数有( ) A.4个 B.3个 C.2个 D.1个 C B D O A E 【关键词】相似三角形判定和性质 【答案】 37.(2009年抚顺市)如图所示,已知点分别是中边的中点,相交于点,,则的长为( ) A F E C B A.4 B.4.5 C.5 D.6 G 【关键词】中位线 二、填空题 1.(2009年重庆市江津区)锐角△ABC中,BC=6,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = , 【关键词】三角形、正方形、二次函数极值 相似 【答案】 2.(2009年滨州)在平面直角坐标系中,顶点的坐标为,若以原点O为位似中心,画的位似图形,使与的相似比等于,则点的坐标为 . 【关键词】三角形位似.. 【答案】(4,6) 3.(2009威海)如图,△ABC与△A′B′C ′是位似图形,点O是位似中心,若OA=2A A′,S△ABC=8,则S△A′B′C ′=________. 【关键词】位似图形 【答案】18 4.(2009年吉林省)如图,的顶点的坐标为(4,0),把沿轴向右平移得到如果那么的长为 . 【关键词】平移,平面直角坐标系内的平移 【答案】7 5.(2009山西省太原市)如图是一种贝壳的俯视图,点分线段近似于黄金分割.已知=10,则的长约为 .(结果精确到0.1) 解析:本题考查黄金分割的有关知识,由题意知, ∴,解得≈6.2,故填6.2.. 【关键词】黄金分割 【答案】6.2. 6.(2009烟台市)如图,与中,交于.给出下列结论: ①; ②; ③; ④. 其中正确的结论是 (填写所有正确结论的序号). 【关键词】全等、相似 【答案】①,③,④ 7.(2009年甘肃庆阳)如图11,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是 . 【关键词】相似三角形判定和性质 【答案】(,0) 8.(2009年广西南宁)三角尺在灯泡的照射下在墙上形成影子(如图6所示).现测得,这个三角尺的周长与它在墙上形成的影子的周长的比是 . 【关键词】投影;相似三角形 【答案】 9.(2009年孝感)如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是 ▲ . 【关键词】相似三角形 【答案】144; 10.(2009年牡丹江市)如图,中,直线交于点交于点交于点若则 . 【关键词】相似三角形的性质 【答案】 11. (2009年日照市)将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是 . 【关键词】相似三角形的性质 【答案】或2; 12.(2009年重庆)已知与相似且面积比为4∶25,则与的相似比为 . 【关键词】相似三角形的性质 【答案】2:5. 13.(2009年莆田)如图,两处被池塘隔开,为了测量两处的距离,在外选一适当的点,连接,并分别取线段的中点,测得=20m,则=__________m. 【关键词】相似三角形 答案:40 14. (2009年牡丹江)如图,中,直线交于点交于点交于点若则 . 【关键词】相似三角形的面积比 【答案】 15.(2009年凉山州)已知且,则= . 【关键词】相似三角形的性质 【答案】 16. (2009年宁德市)如图,△ABC与△DEF是位似图形,位似比为2∶3,已知AB=4,则DE的长为 ____. 【关键词】位似 【答案】6 17.(2009年湖北荆州)如图,已知零件的外径为25,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10,则零件的厚度. 【关键词】相似三角形 【答案】 18.(2009年新疆乌鲁木齐市)如图,在中,,若,则 . 【关键词】相似三角形判定和性质 【答案】8 19. (2009年山西省)如图,与是位似图形,且顶点都在格点上,则位似中心的坐标是 . 【关键词】相似,中心投影 【答案】(9,0) 20. (2009年黄石市)在□ABCD中,在上,若,则 . 【关键词】平行四边形的性质;相似三角形判定和性质 【答案】 21.(2009东营)将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是 . 【关键词】相似三角形 【答案】或2; 三、解答题 1.(2009年台湾) 某校一年级有64人,分成甲、乙、丙三队,其人数比为4:5:7。若由外校转入1人加入 乙队,则后来乙与丙的人数比为何? (A) 3:4 (B) 4:5 (C) 5:6 (D) 6:7 。 【关键词】比例 【答案】A 2.(2009年长春)如图,在矩形中,点分别在边上,,,求的长. 【关键词】矩形的性质、直角三角形的有关计算、相似三角形有关的计算和证明 【答案】 解:∵四边形是矩形,AB=6 ∴∠A=∠D=90°,DC=AB=6 又∵AE=9 ∴在Rt△ABE中,由勾股定理得:BE= ∵, ∴,即 ∴EF= 3.(2009年长春)如图,在中,,分别以为边向外作和,使.延长交边于点,点在两点之间,连结. (1)求证:. (2)当时,求的度数. 【关键词】平行四边形的性质、相似三角形有关的计算和证明 【答案】 (1)证明:在平行四边形ABCD中,AB=DC. 又∵DF=DC, ∴AB=DF. 同理EB=AD. 在平行四边形ABCD中,∠ABC=∠ADC. 又∵∠EBC=∠CDF, ∴∠ABE=∠ADF, ∴△ABE≌△FDA.(4分) (2)解:∵△ABE≌△FDA, ∴∠AEB=∠DAF. ∵∠EBH=∠AEB+∠EAB, ∴∠EBH=∠DAF+∠EAB. ∵AE⊥AF,∴∠EAF=90°. ∵∠BAD=32°, ∴∠DAF+∠EAB=90°-32°=58°, ∴∠EBH=58°. 4.(2009年安徽)如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α, 且DM交AC于F,ME交BC于G. (1)写出图中三对相似三角形,并证明其中的一对; (2)连结FG,如果α=45°,AB=,AF=3,求FG的长. 【关键词】直角三角形的有关计算、相似三角形有关的计算和证明 【答案】 (1)证:△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM(写出两对即可) 以下证明△AMF∽△BGM. ∵∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B ∴△AMF∽△BGM. (2)解:当α=45°时,可得AC⊥BC且AC=BC ∵M为AB的中点,∴AM=BM=分 又∵AMF∽△BGM,∴ ∴ 又,∴, ∴ 5.(2009年郴州市)如图,在ABC中,已知DE∥BC,AD=4,DB=8,DE=3, (1)求的值,(2)求BC的长 【关键词】相似 【答案】解:(1)因为 所以 所以 (2)因为,所以 所以 因为 所以 所以 6.(2009年常德市)如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE,△ABE与△ADC相似吗?请证明你的结论. 【关键词】相似 【答案】 △ABE 与△ADC相似.理由如下: 在△ABE与△ADC中 ∵AE是⊙O的直径, ∴∠ABE=90o, ∵AD是△ABC的边BC上的高, ∴∠ADC=90o, ∴∠ABE=∠ADC. 又∵同弧所对的圆周角相等, ∴∠BEA=∠DCA. ∴△ABE ~△ADC. 7.(2009武汉)如图1,在中,,于点,点是边上一点,连接交于,交边于点. (1)求证:; (2)当为边中点,时,如图2,求的值; (3)当为边中点,时,请直接写出的值. B B A A C O E D D E C O F 图1 图2 F 【关键词】相似三角形的判定和性质 【答案】解:(1),. . , ,. ; B A D E C O F G (2)解法一:作,交的延长线于. ,是边的中点,. 由(1)有,, . ,, 又,. ,. ,,, ,. B A D E C O F 解法二:于, .. 设,则, . , . 由(1)知,设,,. 在中,. .. (3). 8.(2009年上海市)已知∠ABC=90°,AB=2,BC=3,AD∥BC,P为线段BD上的动点,点Q在射线AB上,且满足(如图1所示). (1)当AD=2,且点与点重合时(如图2所示),求线段的长; (2)在图中,联结.当,且点在线段上时,设点之间的距离为,,其中表示△APQ的面积,表示的面积,求关于的函数解析式,并写出函数定义域; (3)当,且点在线段的延长线上时(如图3所示),求的大小. A D P C B Q 图1 D A P C B (Q) ) 图2 图3 C A D P B Q 【关键词】等腰直角三角形 相似三角形 共高三角形的面积 直角三角形相似的判定 【答案】(1)∵Rt△ABD中,AB=2,AD=2, ∴=1,∠D=45° ∴PQ=PC即PB=PC, 过点P作PE⊥BC,则BE=。 而∠PBC=∠D=45° ∴PC=PB= (2)在图8中,过点P作PE⊥BC,PF⊥AB于点F。 ∵∠A=∠PEB=90°,∠D=∠PBE ∴Rt△ABD∽Rt△EPB ∴ 设EB=3k,则EP=4k,PF=EB=3k ∴, = ∴ 函数定义域为 F E F E A D P C B Q 图1 D A P C B (Q) ) 图2 图3 C A D P B Q (3)答:90° 证明:在图8中,过点P作PE⊥BC,PF⊥AB于点F。 ∵∠A=∠PEB=90°,∠D=∠PBE ∴Rt△ABD∽Rt△EPB ∴ ∴= ∴Rt△PQF∽Rt△PCE ∴∠FPQ=∠EPC ∴∠EPC+∠QPE=∠FPQ+∠QPE=90° 8. (2009年陕西省)20.小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下: 如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上). 已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m). 【关键词】利用相似知识测物高 【答案】解:过点D作DG⊥AB,分别交AB、EF于点G、H,则EH=AG=CD=1.2, DH=CE=0.8,DG=CA=30. ∵EF∥AB, ∴. 由题意,知FH=EF-EH=1.7-1.2=0.5. ∴,解之,得BG=18.75. ∴AB=BG+AG=18.75+1.2=19.95≈20.0. ∴楼高AB约为20.0米. 9. (2009年安顺)如图,已知抛物线与交于A(-1,0)、E(3,0)两点,与轴交于点B(0,3)。 (1) 求抛物线的解析式; (2) 设抛物线顶点为D,求四边形AEDB的面积; (3) △AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。 【关键词】待定系数法,相似三角形判定和性质 【答案】(1)∵抛物线与轴交于点(0,3), ∴设抛物线解析式为 根据题意,得,解得 ∴抛物线的解析式为 (5′) (2)(5′)由顶点坐标公式得顶点坐标为(1,4) 设对称轴与x轴的交点为F ∴四边形ABDE的面积= = ==9 (3)似 如图,BD=;∴BE= DE= ∴, 即: ,所以是直角三角形 ∴,且, ∴∽ 10. (2009山西省太原市)甲、乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米,那么路灯甲的高 为 米. 甲 小华乙 解析:本题考查相似的有关知识,设路灯高为米,由相似得 ,解得,所以路灯甲的高为9米,故填9. 【关键词】相似三角形的应用 【答案】9. 11. (2009年浙江省绍兴市)定义一种变换:平移抛物线得到抛物线,使经过的顶点.设的对称轴分别交于点,点是点关于直线的对称点. (1)如图1,若:,经过变换后,得到:,点的坐标为,则①的值等于______________; ②四边形为( ) A.平行四边形 B.矩形 C.菱形 D.正方形 (2)如图2,若:,经过变换后,点的坐标为,求的面积; (3)如图3,若:,经过变换后,,点是直线上的动点,求点到点的距离和到直线的距离之和的最小值. 【关键词】平移变换 【答案】 12.(2009年吉林省)如图,⊙中,弦相交于的中点,连接并延长至点, 使,连接BC、. O F D A E B C (1)求证:; (2)当时,求的值 【关键词】相似三角形判定和性质 【答案】(1)证明: 是的中位线, 又 (2)解:由(1)知, 又 . 13.(2009年宁波市)如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为,直线BC经过点,,将四边形OABC绕点O按顺时针方向旋转度得到四边形,此时直线、直线分别与直线BC相交于点P、Q. (1)四边形OABC的形状是 , 当时,的值是 ; (2)①如图2,当四边形的顶点落在轴正半轴时,求的值; ②如图3,当四边形的顶点落在直线上时,求的面积. (Q) C B A O x P (图3) y Q C B A O x P (图2) y C B A O y x (备用图) (第26题) (3)在四边形OABC旋转过程中,当时,是否存在这样的点P和点Q,使?若存在,请直接写出点P的坐标;若不存在,请说明理由. 【关键词】相似三角形有关的计算和证明 【答案】解:(1)矩形(长方形); . (2)①,, . ,即, ,. 同理, ,即, ,. . ②在和中, . . 设, 在中, ,解得. . (3)存在这样的点和点,使. 点的坐标是,. 对于第(3)题,我们提供如下详细解答,对学生无此要求. 过点画于,连结,则, ,, . 设, Q C B A O x P y H , , ① 如图1,当点P在点B左侧时, , 在中,, Q C B A O x P y H 解得,(不符实际,舍去). , . ②如图2,当点P在点B右侧时, ,. 在中,,解得. , . 综上可知,存在点,,使. 14.(2009年义乌)如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原。 (1)当时,折痕EF的长为;当点E与点A重合时,折痕EF的长为; (2)请写出使四边形EPFD为菱形的的取值范围,并求出当时菱形的边长; (3)令,当点E在AD、点F在BC上时,写出与的函数关系式。当取最大值时,判断与是否相似?若相似,求出的值;若不相似,请说明理由。 温馨提示:用草稿纸折折看,或许对你有所帮助哦! 【关键词】相似三角形 【答案】 解:(1)3, (2). D C B A P E F 图1 当时,如图1,连接, 为折痕,, 令为,则, 在中,, , D C F B A P E O 图2 H 解得,此时菱形边长为. (3)如图2,过作, 易证, , D C (F) H B A P E O 图3 当与点重合时,如图3,连接, ,, . 显然,函数的值在轴的右侧随的增大而增大, 当时,有最大值. 此时,. 综上所述,当取最大值时,,(不写不扣分). 15.(2009恩施市)如图,在中,的面积为25,点为边上的任意一点(不与、重合),过点作,交于点.设,以为折线将翻折(使落在四边形所在的平面内),所得的与梯形重叠部分的面积记为. (1)用表示的面积; (2)求出时与的函数关系式; (3)求出时与的函数关系式; (4)当取何值时,的值最大?最大值是多少? E D B C A B C A 【关键词】相似、二次函数 【答案】解:(1) ∵ DE∥BC ∴∠ADE=∠B,∠AED=∠C ∴△ADE∽△ABC ∴ 即 (2)∵BC=10 ∴BC边所对的三角形的中位线长为5 ∴当0﹤ 时 (3)﹤10时,点A'落在三角形的外部,其重叠部分为梯形 ∵S△A'DE=S△ADE= ∴DE边上的高AH=AH'= 由已知求得AF=5 ∴A'F=AA'-AF=x-5 由△A'MN∽△A'DE知 ∴ (4)在函数中 ∵0﹤x≤5 ∴当x=5时y最大为: 在函数中 当时y最大为: ∵﹤ ∴当时,y最大为: 16.(2009年甘肃庆阳)如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点. △ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F. (1)求证:△ACB∽△DCE;(2)求证:EF⊥AB. 【关键词】相似三角形 【答案】 证明:(1) ∵ ∴ 又 ∠ACB=∠DCE=90°, ∴ △ACB∽△DCE. (2) ∵ △ACB∽△DCE,∴ ∠ABC=∠DEC. 又 ∠ABC+∠A =90°,∴ ∠DEC+∠A=90°. ∴ ∠EFA=90°. ∴ EF⊥AB. 7.(2009泰安)将一个量角器和一个含30度角的直角三角板如图(1)放置,图(2)是由他抽象出的几何图形,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OD。 (1) 求证:DB∥CF。 (1) 当OD=2时,若以O、B、F为顶点的三角形与△ABC相似,求OB。 【关键词】相似、切线 【答案】证明: (1)连接OF,如图 ∵AB且半圆O于F, ∴OF⊥AB。 ∵CB⊥AB ,∴BC∥OF。 ∵BC=OD,OD=OF, ∴BC=OF。 ∴四边形OBCF是平行四边形, ∴DB∥CF。 (2) ∵以O、B、F为顶点的三角形与△ABC相似,∠OFB=∠ABC=90°, ∴∠A∠OBF∠BOF ∵∠OBF=∠BFC,∠BFC>∠A, ∴∠OBF>∠A ∴∠OBF与∠A不可能是对顶角。 ∴∠A与∠BOF是对应角。 ∴∠BOF=30° ∴OB=OF/cos30°= 18.(2009泰安)如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F。 (1) 求证:FD2=FB●FC。 (2) 若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由。 【关键词】相似、垂直 【答案】证明:(1)∵E是Rt△ACD斜边中点 ∴DE=EA ∴∠A=∠2 ∵∠1=∠2 ∴∠1=∠A… ∵∠FDC=∠CDB+∠1=90°+∠1,∠FBD=∠ACB+∠A=90°+∠A ∴∠FDC=∠FBD ∵F是公共角 ∴△FBD∽△FDC ∴ ∴ (2)GD⊥EF 理由如下: ∵DG是Rt△CDB斜边上的中线, ∴DG=GC ∴∠3=∠4 由(1)得∠4=∠1 ∴∠3=∠1 ∵∠3+∠5=90° ∴∠5+∠1=90° ∴DG⊥EF 19、(2009江西)问题背景 在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息: 甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm. 乙组:如图2,测得学校旗杆的影长为900cm. 丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm. 任务要求 (1)请根据甲、乙两组得到的信息计算出学校旗杆的高度; (2)如图3,设太阳光线与相切于点.请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段的影长;需要时可采用等式). D D F E 900cm 图2 B C A 60cm 80cm 图1 G H NE 156cm ME OE 200cm 图3 KE 【关键词】相似、光影 【答案】解:(1)由题意可知: ∴ ∴即 ∴DE=1200(cm). 所以,学校旗杆的高度是12m. (2)解法一: 与①类似得:即 ∴GN=208. 在中,根据勾股定理得: ∴NH=260. 设的半径为rcm,连结OM, ∵NH切于M,∴ 则又 ∴∴ 又. ∴解得:r=12. 所以,景灯灯罩的半径是12cm. D D F E 900cm 图2 B C A 60cm 80cm 图1 图3 G H NE 156cm ME OE 200cm KE 解法二: 与①类似得:即 ∴GN=208. 设的半径为rcm,连结OM, ∵NH切于M,∴ 则又 ∴ ∴即 ∴又. 在中,根据勾股定理得: 即 解得:(不合题意,舍去) 所以,景灯灯罩的半径是12cm. 20. (2009年湘西自治州如图,在△ABC中,DE∥BC,EF∥AB, 求证:△ADE∽△EFC. 【关键词】相似三角形的判定和判定 【答案】证明:∵DE∥BC,∴DE∥FC,∴∠AED=∠C 又∵EF∥AB,∴EF∥AD,∴∠A=∠FEC ∴△ADE∽△EFC 21. (2009年清远)如图,已知是的直径,过点作弦的平行线,交过点的切线于点,连结. (1)求证:; (2)若,,求的长. 【关键词】相似三角形有关的计算和证明 【答案】(1)证明: 是直径 是的切线,切点为 (2) 22.(2009年清远)如图,已知一个三角形纸片,边的长为8,边上的高为,和都为锐角,为一动点(点与点不重合),过点作,交于点,在中,设的长为,上的高为. (1)请你用含的代数式表示. (2)将沿折叠,使落在四边形所在平面,设点落在平面的点为,与四边形重叠部分的面积为,当为何值时,最大,最大值为多少? 【关键词】分类讨论思想 【答案】解:(1) (2) 的边上的高为, 当点落在四边形内或边上时, =(0) 当落在四边形外时,如下图, 设的边上的高为, 则 所以 综上所述:当时,,取, 当时,, 取, 当时,最大, M N C B E F A A1 23. (2009年济宁市)如图,中,,,.半径为1的圆的圆心以1个单位/的速度由点沿方向在上移动,设移动时间为(单位:). (1)当为何值时,⊙与相切; (2)作交于点,如果⊙和线段交于点,证明:当时,四边形为平行四边形. 【关键词】相似 【答案】(1)解:当⊙在移动中与相切时,设切点为,连, 则. ∴∽.∴. ∵,, ∴.∴. (2)证明:∵,,∴∥. 当时,. ∴.∴. ∴. ∵∽,∴.∴, ∴.∴. ∴当时,四边形为平行四边形. 24.(2009年宜宾)如图,公园内有一个长5米的跷跷板AB,当支点O在距离A端2米时,A端的人可以将B端的人跷高1.5米,那么当支点O在AB的中点时,A端的人下降同样的高度可以将B端的人跷高 米. 【关键词】相似三角形的性质 【答案】1. 25.(2009年广西钦州)已知:如图,在△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D. (1)求证:BC=CD; (2)求证:∠ADE=∠ABD; (3)设AD=2,AE=1,求⊙O直径的长. 【关键词】切线长定理、相似三角形. 【答案】 解:(1)∵∠ABC=90°, ∴OB⊥BC. ∵OB是⊙O的半径, ∴CB为⊙O的切线. 又∵CD切⊙O于点D, ∴BC=CD; (2)∵BE是⊙O的直径, ∴∠BDE=90°. ∴∠ADE+∠CDB =90°. 又∵∠ABC=90°, ∴∠ABD+∠CBD=90°. 由(1)得BC=CD,∴∠CDB =∠CBD. ∴∠ADE=∠ABD; (3)由(2)得,∠ADE=∠ABD,∠A=∠A. ∴△ADE∽△ABD. ∴=. ∴=,∴BE=3, ∴所求⊙O的直径长为3. 26.(2009年广西钦州)如图,已知抛物线y=x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1. (1)填空:点C的坐标是_▲_,b=_▲_,c=_▲_; (2)求线段QH的长(用含t的式子表示); (3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由. 【关键词】二次函数、相似三角形. 【答案】 解:(1)(0,-3),b=-,c=-3. (2)由(1),得y=x2-x-3,它与x轴交于A,B两点,得B(4,0). ∴OB=4,又∵OC=3,∴BC=5. 由题意,得△BHP∽△BOC, ∵OC∶OB∶BC=3∶4∶5, ∴HP∶HB∶BP=3∶4∶5, ∵PB=5t,∴HB=4t,HP=3t. ∴OH=OB-HB=4-4t. 由y=x-3与x轴交于点Q,得Q(4t,0). ∴OQ=4t. ①当H在Q、B之间时, QH=OH-OQ =(4-4t)-4t=4-8t. ②当H在O、Q之间时, QH=OQ-OH =4t-(4-4t)=8t-4. 综合①,②得QH=|4-8t|; (3)存在t的值,使以P、H、Q为顶点的三角形与△COQ相似. ①当H在Q、B之间时,QH=4-8t, 若△QHP∽△COQ,则QH∶CO=HP∶OQ,得=, ∴t=. 若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得=, 即t2+2t-1=0. ∴t1=-1,t2=--1(舍去). ②当H在O、Q之间时,QH=8t-4. 若△QHP∽△COQ,则QH∶CO=HP∶OQ,得=, ∴t=. 若△PHQ∽△COQ,则PH∶CO=HQ∶OQ,得=, 即t2-2t+1=0. ∴t1=t2=1(舍去). 综上所述,存在的值,t1=-1,t2=,t3=. 27.(2009年莆田)已知,如图1,过点作平行于轴的直线,抛物线上的两点的横坐标分别为1和4,直线交轴于点,过点分别作直线的垂线,垂足分别为点、,连接. (1)求点的坐标; (2)求证:; (3)点是抛物线对称轴右侧图象上的一动点,过点作交轴于点,是否存在点使得与相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由. 【关键词】二次函数、抛物线、一次函数、相似三角形 (1)解:方法一,如图1,当时, 当时, ∴ 设直线的解析式为 则 解得 ∴直线的解析式为 当时, 方法二:求两点坐标同方法一,如图2,作,,垂足分别为、,交轴于点,则四边形和四边形均为矩形,设 3分 E D C A F B x O y l (图2) G H M 解得 (2)证明:方法一:在中, 在中, 由(1)得 方法二:由 (1)知 同理: 同理: 即 (3)存在. 解:如图3,作轴,垂足为点 9分 E D C O F x y 图3 M P l Q 又 设,则 ①当时, 解得 ②当时, 解得 综上,存在点、使得与相似. 14分 28.(2009年包头)如图,已知是的直径,点在上,过点的直线与的延长线交于点,,. (1)求证:是的切线; (2)求证:; (3)点是的中点,交于点,若,求的值. 【关键词】圆、切线 解: (1), 又, . 又是的直径, , ,即, 而是的半径, 是的切线. (2), , 又, .) (3)连接, 点是的中点,,, 而,,而, ,,, 又是的直径,, . ,. 29. (2009肇庆).如图 ,在中,,线段 AB 的垂直平分线交 AB于 D,交 AC 于 E,连接BE. (1)求证:∠CBE=36°; (2)求证:. 【关键词】三角形相似 【答案】证明:(1)∵DE是AB的垂直平分线,∴, ∴.∵,∴.∴.(2)由(1)得,在△BCE中,, ∴,∴.在△ABC 与△BEC中,,, ∴. ∴,即. 故. 30. (2009年南充)如图,半圆的直径,点C在半圆上,. (1)求弦的长; (2)若P为AB的中点,交于点E,求的长. 【关键词】圆的性质,三角形相似的性质 【答案】解:是半圆的直径,点在半圆上, . 在中, (2), ., . 又, , . 31.(2009年温州)如图,在平面直角坐标系中,直线AB与Y轴和X轴分别交于点A、点8,与反比例函数y一罟在第一象限的图象交于点c(1,6)、点D(3,x).过点C作CE上y轴于E,过点D作DF上X轴于F. (1)求m,n的值; (2)求直线AB的函数解析式; (3)求证:△AEC∽△DFB. 【关键词】反比例函数的定义,待定系数法确定一次函数的解析式,相似的判定 【答案】解:(1)由题意得1= ∴m=6 ∴n= ∴n=2 (2)设直线AB的函数解析式为y=kx+b 由题意得 解得 ∴直线AB的函数解析式为y=-2x+8。 (3)∵y=-2x+8 ∴A(0,8),B(4,0) ∵CE⊥y轴,DF⊥x轴, ∴∠AEC=∠DFB=Rt∠ ∵AE=DF=2,CE=BF=1, ∴△AEC≌△DFB。 32.(2009年温州)如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连结DE. ’ (1)当BD=3时,求线段DE的长; (2)过点E作半圆O的切线,当切线与AC边相交时,设交点为F.求证:△FAE是等腰三角形. 【关键词】直角三角形、圆的性质,相似的判定,切线的性质,等腰三角形的判定 【答案】解:(1)∵∠C=90°,AC=3,BC=4, ∴AB=5, ∵DB为直径, ∴∠DEB=∠C=90°, 又∵∠B=∠B ,∴△DBE∽△ABC ∴ 即 ∴DE=。 (2)解法一:连结OE, ∵EF为半圆O的切线, ∴∠DEO+∠DEF=90°, ∵∠AEF+∠DEF=90°, ∴∠AEF=∠DEO, ∵△DBE∽△ABC, ∴∠A=∠EDB, 又∵∠EDO=∠DEO, ∴∠AEF=∠A, ∴△FAE是等腰三角形。 解法二:连结OE, ∵EF为半圆O的切线, ∴∠AEF+∠OEB=90°, ∵∠C=90°, ∴∠A+∠B=90°, ∵OE=OB ∴∠OEB=∠B, ∴∠AEF=∠A ∴△FAE是等腰三角形。 33(2009临沂)如图,抛物线经过三点. (1)求出抛物线的解析式; (2)P是抛物线上一动点,过P作轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由; (3)在直线AC上方的抛物线上有一点D,使得的面积最大,求出点D的坐标. 【关键词】抛物线的解析式,相似的性质,二次函数的最值问题 【答案】解:(1)该抛物线过点,可设该抛物线的解析式为. 将,代入, 得解得 此抛物线的解析式为. (2)存在. 如图,设点的横坐标为, 则点的纵坐标为, 当时, ,. 又, ①当时, , 即. 解得(舍去),. ②当时,,即. 解得,(均不合题意,舍去) 当时,. 类似地可求出当时,. 当时,. 综上所述,符合条件的点为或或. (3)如图,设点的横坐标为,则点的纵坐标为. 过作轴的平行线交于. 由题意可求得直线的解析式为. 点的坐标为. . . 当时,面积最大. . 34.(2009年中山)正方形边长为4,、分别是、上的两个动点,当点在上运动时,保持和垂直, (1)证明:; (2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积; (3)当点运动到什么位置时,求的值. 【关键词】相似三角形有关的计算和证明 【答案】(1)在正方形中,, , , . 在中,, , . (2), , , , 当时,取最大值,最大值为10. (3), 要使,必须有, 由(1)知, , 当点运动到的中点时,,此时. x y A D B O C 35.(2009年牡丹江)如图,在平面直角坐标系中,若、的长是关于的一元二次方程的两个根,且 (1)求的值. (2)若为轴上的点,且求经过、两点的直线的解析式,并判断与是否相似? (3)若点在平面直角坐标系内,则在直线上是否存在点使以、、、为顶点的四边形为菱形?若存在,请直接写出点的坐标;若不存在,请说明理由. 【关键词】三角函数,一次函数,菱形,相似三角形的综合应用 【答案】(1)解得 在中,由勾股定理有 (2)∵点在轴上, 由已知可知D(6,4) 设当时有 解得 同理时, 在中, 在中, (3)满足条件的点有四个 36. (2009年凉山州)如图,在方格纸中 (1)请在方格纸上建立平面直角坐标系,使,并求出点坐标; (2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形; A B C (3)计算的面积. 【关键词】位似、相似比、面积 【答案】(1)画出原点,轴、轴., (2)画出图形. (3). 37. (2009年济宁市)如图,中,,,.半径为1的圆的圆心以1个单位/的速度由点沿方向在上移动,设移动时间为(单位:). (1)当为何值时,⊙与相切; (2)作交于点,如果⊙和线段交于点,证明:当时,四边形为平行四边形. · 图1 图2 【关键词】相似 【答案】(1)解:当⊙在移动中与相切时,设切点为,连, 则. ∴∽.∴. ∵,, ∴.∴. (2)证明:∵,,∴∥. 当时,. ∴.∴. ∴. ∵∽,∴.∴, ∴.∴. ∴当时,四边形为平行四边形. 38. (2009年宁德市)如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG. (1)连接GD,求证:△ADG≌△ABE; (2)连接FC,观察并猜测∠FCN的度数,并说明理由; (3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN 的大小发生改变,请举例说明. N M B E C D F G 图(1) 【关键词】四边形中三角形全等和相似的运用 M B E A C N D F G 图(1) H 解:(1)∵四边形ABCD和四边形AEFG是正方形 ∴AB=AD,AE=AG,∠BAD=∠EAG=90º ∴∠BAE+∠EAD=∠DAG+∠EAD ∴∠BAE=∠DAG ∴△ BAE≌△DAG (2)∠FCN=45º 理由是:作FH⊥MN于H ∵∠AEF=∠ABE=90º ∴∠BAE +∠AEB=90º,∠FEH+∠AEB=90º ∴∠FEH=∠BAE 又∵AE=EF,∠EHF=∠EBA=90º ∴△EFH≌△ABE ∴FH=BE,EH=AB=BC,∴CH=BE=FH ∵∠FHC=90º,∴∠FCH=45º (3)当点E由B向C运动时,∠FCN的大小总保持不变, 理由是:作FH⊥MN于H 由已知可得∠EAG=∠BAD=∠AEF=90º 结合(1)(2)得∠FEH=∠BAE=∠DAG 又∵G在射线CD上 ∠GDA=∠EHF=∠EBA=90º ∴△EFH≌△GAD,△EFH∽△ABE ∴EH=AD=BC=b,∴CH=BE, ∴== ∴在Rt△FEH中,tan∠FCN=== ∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN= 39.(2009年潍坊)已知,延长BC到D,使.取的中点,连结交于点. (1)求的值; (2)若,求的长. 解:(1) 过点F作,交于点. 为的中点 为的中点,. 由,得, (2) 又 . 40.(2009年咸宁市)如图,将矩形沿对角线剪开,再把沿方向平移得到. (1)证明; C B A D (2)若,试问当点在线段上的什么位置时,四边形是菱形,并请说明理由. 40. (09湖南怀化)如图,直线经过⊙上的点,并且⊙交直线于、两点,连接,,.求证:(1); (2)∽. 【关键词】圆的基本性质、切线定理 【答案】证明:(1)∵OE=OD,∴△ODE是等腰三角形, 又EC=DC,∴C是底边DE上的中点, ∴ (2)∵AB是直径,∴∠ACB=, ∴∠B+∠BAC=, 又∠DCA+∠ACO=,∠ACO=∠BAC, ∴∠DCA=∠B.又∠ADC=∠CDB, ∴△ACD∽△CBD. 41.(09湖南怀化)如图11,已知二次函数的图象与轴相交于两个不同的点、,与轴的交点为.设的外接圆的圆心为点. (1)求与轴的另一个交点D的坐标; (2)如果恰好为的直径,且的面积等于,求和的值. 【关键词】圆的基本性质、三角形相似的判定和性质 【答案】解 (1)易求得点的坐标为 由题设可知是方程即 的两根, 所以, 所 如图3,∵⊙P与轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连结DB,∴△AOC∽△DOC,则 由题意知点在轴的负半轴上,从而点D在轴的正半轴上, 所以点D的坐标为(0,1) (2)因为AB⊥CD, AB又恰好为⊙P的直径,则C、D关于点O对称, 所以点的坐标为,即 又, 所以解得 42.(09湖北宜昌)(09湖北宜昌)已知:如图1,把矩形纸片ABCD折叠,使得顶点A与边DC上的动点P重合(P不与点D,C重合), MN为折痕,点M,N分别在边BC, AD上,连接AP,MP,AM, AP与MN相交于点F.⊙O过点M,C,P. (1)请你在图1中作出⊙O(不写作法,保留作图痕迹); (2)与 是否相等?请你说明理由; (3)随着点P的运动,若⊙O与AM相切于点M时,⊙O又与AD相切于点H. 设AB为4,请你通过计算,画出这时的图形.(图2,3供参考) 图1 图2 图3 【关键词】矩形的性质与判定、线段的比和比例线段 【答案】解:(1)如图; (2)与不相等. 假设,则由相似三角形的性质,得MN∥DC. ∵∠D=90°,∴DC⊥AD,∴MN⊥AD. ∵据题意得,A与P关于MN对称,∴MN⊥AP. ∵据题意,P与D不重合, ∴这与“过一点(A)只能作一条直线与已知直线(MN)垂直”矛盾. ∴假设不成立. ∴不成立. (2) 解法2:与不相等. 理由如下: ∵P, A关于MN对称,∴MN垂直平分AP. ∴cos∠FAN=. ∵∠D=90°, ∴cos∠PAD=. ∵∠FAN=∠PAD,∴=. ∵P不与D重合,P在边DC上;∴AD≠AP. ∴≠;从而≠. (3)∵AM是⊙O的切线,∴∠AMP=90°, ∴∠CMP+∠AMB=90°. ∵∠BAM+∠AMB=90°,∴∠CMP=∠BAM. ∵MN垂直平分,∴MA=MP, ∵∠B=∠C=90°, ∴△ABM≌△MCD. ∴MC=AB=4, 设PD=x,则CP=4-x, ∴BM=PC=4-x. (5分) 连结HO并延长交BC于J. ∵AD是⊙O的切线,∴∠JHD=90°. ∴矩形HDCJ. (7分) ∴OJ∥CP, ∴△MOJ∽△MPC, ∴OJ:CP=MO:MP=1:2, ∴OJ=(4-x),OH=MP=4-OJ=(4+x). ∵MC2= MP2-CP2,∴(4+x)2-(4-x)2=16. 解得:x=1.即PD=1,PC=3, ∴BC=BM+MC=PC+AB=3+4=7. 由此画图(图形大致能示意即可). (3)解法2: 连接HO,并延长HO交BC于J点,连接AO. 由切线性质知,JH⊥AD,∵BC∥AD,∴HJ⊥BC, ∴OJ⊥MC,∴MJ=JC. ∵AM,AH与⊙O相切于点M,H, ∴∠AMO=∠AHO=90°, ∵OM=OH, AO=AO, ∴Rt△AMO≌Rt△AHO. ∴设AM=x,则 AM=AH=x, 由切线性质得,AM⊥PM, ∴∠AMP=90°,∴∠BMA+∠CMP=90°. ∵∠BMA+∠BAM=90°,∴∠BAM=∠CMP , ∵∠B=∠MCP=90°, ∵MN为AP的中垂线,∴AM=MP. ∴△ABM≌△MCP . ∴四边形ABJH为矩形,得BJ=AH=x, Rt△ABM中,BM=, ∴MJ==JC,(9分) ∴AB=MC.∴4=2(),∴ ∴AD=BC==7, ∴PC==3. 由此画图(图形大致能示意即可). 43. (2009年湖北荆州)21.(7分)如图,AB是半圆O的直径,C为半圆上一点,N是线段 BC上一点(不与B﹑C重合),过N作AB的垂线交AB于M, 交AC的延长线于E,过C点作半圆O的切线交EM于F. ⑴求证:△ACO∽△NCF; ⑵若NC∶CF=3∶2,求sinB 的值. 【关键词】相似三角形综合 【答案】 44.(2009年茂名市)如图,在中,点是边上的动点(点与点不重合),过动点作交于点 (1)若与相似,则是多少度? (2分) (2)试问:当等于多少时,的面积最大?最大面积是多少? (4分) (3)若以线段为直径的圆和以线段为直径的圆相外切,求线段的长.(4分) 【关键词】二次函数、圆、相似综合题 【答案】(1)当△ABC 与△DAP 相似时,∠APD的度数是60°或30°. (2)设,∵,,∴, 又∵,∴,, ∴,而, ∴ . ∴PC 等于12时,的面积最大,最大面积是. (3)设以和为直径的圆心分别为、,过 作 于点, 设的半径为,则.显然,,∴,∴, ∴, , 又∵和外切, ∴. 在中,有, ∴, 解得:, ∴. 45.(2009年湖北十堰市)如图①,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F. (1) 求证:DE-BF = EF. (2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系, 并说明理由. (3) 若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明). 【关键词】正方形的性质与判定、多边形相似 【答案】(1) 证明: ∵ 四边形ABCD 是正方形, BF⊥AG , DE⊥AG ∴ DA=AB, ∠BAF + ∠DAE = ∠DAE + ∠ADE = 90° ∴ ∠BAF = ∠ADE ∴ △ABF ≌ △DAE ∴ BF = AE , AF = DE ∴ DE-BF = AF-AE = EF (2)EF = 2FG 理由如下: ∵ AB⊥BC , BF⊥AG , AB =2 BG ∴ △AFB ∽△BFG ∽△ABG ∴ ∴ AF = 2BF , BF = 2 FG 由(1)知, AE = BF,∴ EF = BF = 2 FG (3) 如图 DE + BF = EF 46.(2009年山东青岛市)如图,在梯形ABCD中,,,,,点由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交于Q,连接PE.若设运动时间为(s)().解答下列问题: (1)当为何值时,? (2)设的面积为(cm2),求与之间的函数关系式; (3)是否存在某一时刻,使?若存在,求出此时的值;若不存在,说明理由. (4)连接,在上述运动过程中,五边形的面积是否发生变化?说明理由. 【关键词】全等三角形的性质与判定、相似三角形判定和性质、平行四边形有关的计算 【答案】解:(1)∵ ∴. 而, ∴, ∴. ∴当. (2)∵平行且等于, ∴四边形是平行四边形. ∴. ∵, ∴. ∴. ∴. . ∴. 过B作,交于,过作,交于. . ∵, ∴. 又, , , . (3). 若, 则有, 解得. (4)在和中, ∴ . ∴在运动过程中,五边形的面积不变. 47.(2009年广东省)正方形边长为4,、分别是、上的两个动点, 当点在上运动时,保持和垂直, (1)证明:; (2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积; (3)当点运动到什么位置时,求此时的值. 【关键词】 正方形的性质;相似三角形判定和性质;直角梯形;与二次函数有关的面积问题;二次函数的极值问题;相似三角形有关的计算和证明 【答案】 解:(1)在正方形中, , , , , 在中,, , , (2), , , , 当时,取最大值,最大值为10. (3), 要使,必须有, 由(1)知, , 当点运动到的中点时,,此时. 48.(2009年山西省)如图,已知直线与直线相交于点分别交轴于两点.矩形的顶点分别在直线上,顶点都在轴上,且点与点重合. (1)求的面积; (2)求矩形的边与的长; (3)若矩形从原点出发,沿轴的反方向以每秒1个单位长度的速度平移,设移动时间为秒,矩形与重叠部分的面积为,求关于的函数关系式,并写出相应的的取值范围. A D B E O C F x y y (G) 【关键词】一次函数的几何应用;一次函数与二元一次方程;矩形的性质;特殊平行四边形相关的面积问题;相似三角形有关的计算 【答案】(1)解:由得点坐标为 由得点坐标为 ∴ 由解得∴点的坐标为 ∴ (2)解:∵点在上且 ∴点坐标为 又∵点在上且 ∴点坐标为 ∴ (3)解法一:当时,如图1,矩形与重叠部分为五边形(时,为四边形).过作于,则 A D B E O R F x y y M (图3) G C A D B E O C F x y y G (图1) R M A D B E O C F x y y G (图2) R M ∴即∴ ∴ 即 当时,如图2,为梯形面积,∵G(8-t,0)∴GR=, ∴ 当时,如图3,为三角形面积, 49.(2009 黑龙江大兴安岭)已知:在中,,动点绕的顶点逆时针旋转,且,连结.过、的中点、作直线,直线与直线、分别相交于点、. 图2 图3 图1 (N) (1)如图1,当点旋转到的延长线上时,点恰好与点重合,取的中点,连结、,根据三角形中位线定理和平行线的性质,可得结论(不需证明). (2)当点旋转到图2或图3中的位置时,与有何数量关系?请分别写出猜想,并任选一种情况证明. 【关键词】三角形中位线、平行线的性质、阅读理解题 【答案】图2: 图3: 证明:如图2,取的中点,连结、 ∵是的中点,是的中点, ∴,, ∴. 同理,,, ∴ ∵, ∴, ∴ ∴. 证明图3的过程与证明图2过程给分相同. 50. (2009年崇左)如图,中,分别是边的中点,相交于.求证:. B C D G E A 【关键词】三角形的相似。利用中点做辅助线可得。连接两中点可利用中位线知识得到其结果。 【答案】 B C D G E A 证明:连结, 分别是边的中点, , , , . 51. (2009东营)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. (1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积; (2)设MN与AB之间的距离为米,试将△EMN的面积S(平方米)表示成关于x的函数; (3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由. 【关键词】二次函数与面积,相似 【答案】解:(1)由题意,当MN和AB之间的距离为0.5米时,MN应位于DC下方,且此时△EMN中MN边上的高为0.5米. 所以,S△EMN= =0.5(平方米). 即△EMN的面积为0.5平方米. (2)①如图1所示,当MN在矩形区域滑动, 即0<x≤1时, △EMN的面积S= = ; ②如图2所示,当MN在三角形区域滑动, 即1<x< 时, 如图,连接EG,交CD于点F,交MN于点H, ∵ E为AB中点, ∴ F为CD中点,GF⊥CD,且FG= . 又∵ MN∥CD, ∴ △MNG∽△DCG. ∴ ,即 .……4分 故△EMN的面积S= = ; 综合可得: (3)①当MN在矩形区域滑动时, ,所以有 ; ②当MN在三角形区域滑动时,S= . 因而,当 (米)时,S得到最大值, 最大值S= = = (平方米). ∵ , ∴ S有最大值,最大值为 平方米. 52.(2009年枣庄市)宽与长的比是的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示): 第一步:作一个正方形ABCD; 第二步:分别取AD,BC的中点M,N,连接MN; 第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E; 第四步:过E作EF⊥AD,交AD的延长线于F. 请你根据以上作法,证明矩形DCEF为黄金矩形. A B C D E F M N 【关键词】黄金矩形 【答案】证明:在正方形ABCD中,取, ∵ N为BC的中点, ∴ . 在中, . 又∵ , ∴ . ∴ . 故矩形DCEF为黄金矩形. 53. (2009年厦门市)已知:在中,. (1)设的周长为,,(≤≤).写出关于的函数关系式,并在直角坐标系中画出此函数的图象; (2)如图,是线段上一点,连接,若.求证:. 【关键词】一次函数的图象,相似三角形 【答案】(1)解:y=7-2x(2≤x≤3) 画直角坐标系 画线段 (2)证明:∵ AB=AC,∴ ∠B=∠C. ∵ ∠B=∠BAD,∴ ∠BAD=∠C. 又∵ ∠B=∠B, ∴. 【关键词】三角形三边关系 【答案】B 54.(2009年赤峰市)如图,一次函数y=ax+b的图象与反比例函数y=k/x的图象交于A、B、两点,与x轴交于点C,与y轴交于点D,已知OA= ,tan∠AOC=1/3,点B的坐标为(m,-2)。 (1)求反比例函数的解析式 (2)求一次函数的解析式 (3)在y轴上存在一点P,是的△PDC与△ODC相似, 请你求出P点的坐标。 55.(2009年绵阳市)如图,A、P、B、C是⊙O上的四点,∠APC =∠BPC = 60°, AB与PC交于Q点. Q P C B A O (1)判断△ABC的形状,并证明你的结论; (2)求证:; (3)若∠ABP = 15°,△ABC的面积为4,求PC的长. 【关键词】圆的性质,相似三角形,三角函数 【答案】(1) ∵ ∠ABC =∠APC = 60°,∠BAC =∠BPC = 60°, ∴ ∠ACB = 180°-∠ABC-∠BAC = 60°, ∴ △ABC是等边三角形. (2)如图,过B作BD∥PA交PC于D,则 ∠BDP =∠APC = 60°. 又 ∵ ∠AQP =∠BQD,∴ △AQP∽△BQD, . ∵ ∠BPD =∠BDP = 60°, ∴ PB = BD. ∴ . (3)设正△ABC的高为h,则 h = BC· sin 60°. ∵ BC · h = 4, 即BC · BC· sin 60° = 4,解得BC = 4. 连接OB,OC,OP,作OE⊥BC于E. 由△ABC是正三角形知∠BOC = 120°,从而得∠OCE = 30°, ∴ . 由∠ABP = 15° 得 ∠PBC =∠ABC +∠ABP = 75°,于是 ∠POC = 2∠PBC = 150°. ∴ ∠PCO =(180°-150°)÷2 = 15°. 如图,作等腰直角△RMN,在直角边RM上取点G,使∠GNM = 15°,则∠RNG = 30°,作GH⊥RN,垂足为H.设GH = 1,则 cos∠GNM = cos15° = MN. ∵ 在Rt△GHN中,NH = GN · cos30°,GH = GN · sin30°. 于是 RH = GH,MN = RN · sin45°,∴ cos15° =. 在图中,作OF⊥PC于E,∴ PC = 2FD = 2 OC ·cos15° =. 56.(2009年梅州市)如图 ,梯形ABCD中,,点在上,连与的延长线交于点G. (1)求证:; D C F E A B G (2)当点F是BC的中点时,过F作交于点,若,求的长. 【关键词】相似三角形 【答案】(1)证明:∵梯形,, ∴, ∴. (2) 由(1), 又是的中点, ∴, ∴ 又∵,, ∴,得. ∴, ∴. 查看更多