2020高中数学 第一章函数的单调性与导数

2020高中数学 第一章函数的单调性与导数

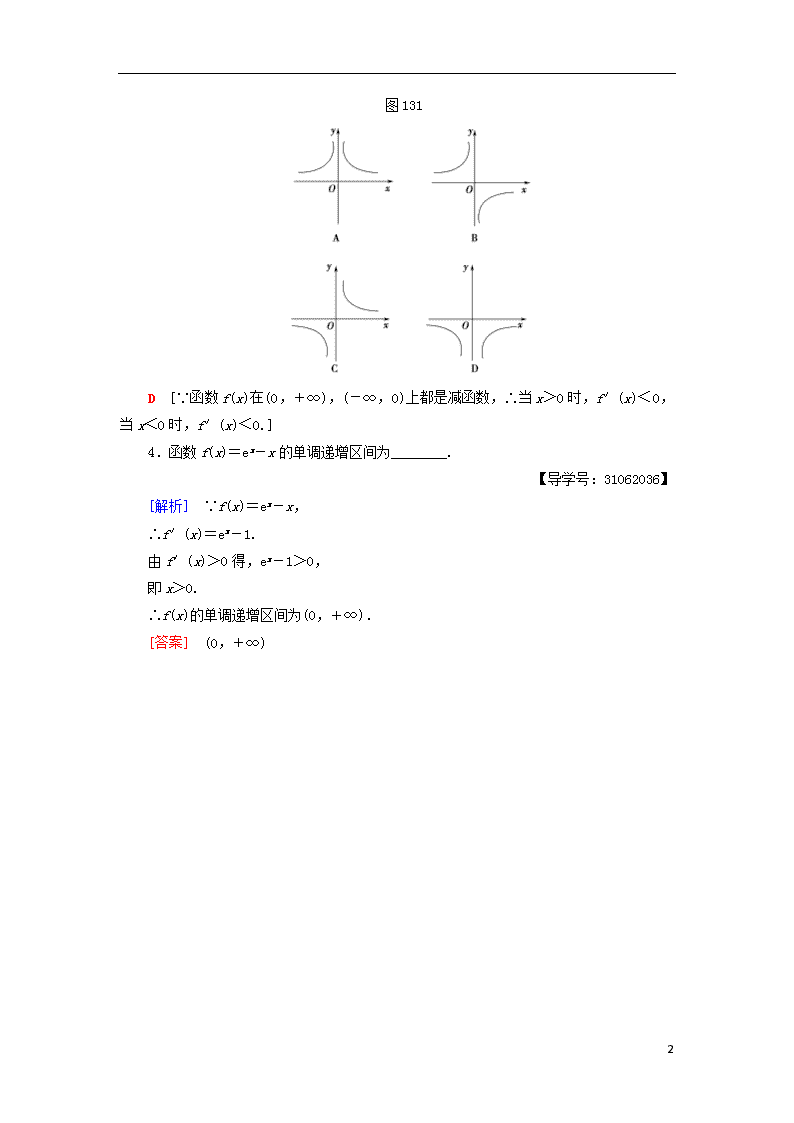
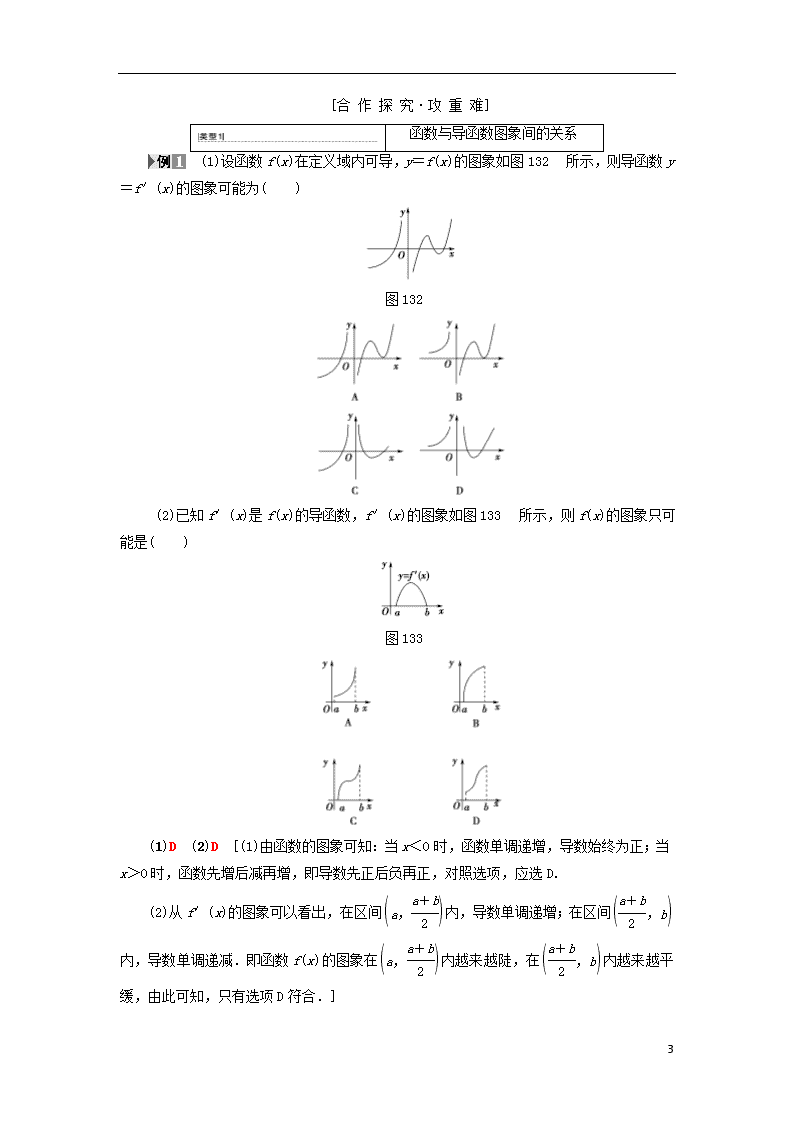
‎1.3.1　‎函数的单调性与导数 学习目标：1.理解导数与函数的单调性的关系．(易混点)2.掌握利用导数判断函数单调性的方法．(重点)3.会用导数求函数的单调区间．(重点、难点)‎ ‎[自 主 预 习·探 新 知]‎ ‎1．函数的单调性与其导数正负的关系 定义在区间(a，b)内的函数y＝f(x)：‎ f′(x)的正负 f(x)的单调性 f′(x)＞0‎ 单调递增 f′(x)＜0‎ 单调递减 思考：如果在某个区间内恒有f′(x)＝0，那么函数f(x)有什么特性？‎ ‎[提示]f(x)是常数函数．‎ ‎2．函数图象的变化趋势与导数值大小的关系 一般地，设函数y＝f(x)，在区间(a，b)上：‎ 导数的绝对值 函数值变化 函数的图象 越大 快 比较“陡峭”(向上或向下)‎ 越小 慢 比较“平缓”(向上或向下)‎ ‎[基础自测]‎ ‎1．思考辨析 ‎(1)函数f(x)在定义域上都有f′(x)>0，则函数f(x)在定义域上单调递增．(　　)‎ ‎(2)函数在某一点的导数越大，函数在该点处的切线越“陡峭”．(　　)‎ ‎(3)函数在某个区间上变化越快，函数在这个区间上导数的绝对值越大．(　　)‎ ‎[答案]　(1)×　(2)×　(3)√‎ ‎2．函数f(x)＝2x－sin x在(－∞，＋∞)上是(　　)‎ A．增函数　　 B．减函数 C．先增后减 D．不确定 A　[∵f(x)＝2x－sin x，‎ ‎∴f′(x)＝2－cos x＞0在(－∞，＋∞)上恒成立，‎ ‎∴f(x)在(－∞，＋∞)上是增函数．]‎ ‎3．函数y＝f(x)的图象如图131所示，则导函数y＝f′(x)的图象可能是(　　)‎ 9‎ 图131‎ D　[∵函数f(x)在(0，＋∞)，(－∞，0)上都是减函数，∴当x＞0时，f′(x)＜0，当x＜0时，f′(x)＜0.]‎ ‎4．函数f(x)＝ex－x的单调递增区间为________. ‎ ‎【导学号：31062036】‎ ‎[解析]　∵f(x)＝ex－x，‎ ‎∴f′(x)＝ex－1.‎ 由f′(x)＞0得，ex－1＞0，‎ 即x＞0.‎ ‎∴f(x)的单调递增区间为(0，＋∞)．‎ ‎[答案]　(0，＋∞)‎ 9‎ ‎[合 作 探 究·攻 重 难]‎ 函数与导函数图象间的关系 ‎　(1)设函数f(x)在定义域内可导，y＝f(x)的图象如图132所示，则导函数y＝f′(x)的图象可能为(　　)‎ 图132‎ ‎ (2)已知f′(x)是f(x)的导函数，f′(x)的图象如图133所示，则f(x)的图象只可能是(　　)‎ 图133‎ ‎(1)D　(2)D　[(1)由函数的图象可知：当x＜0时，函数单调递增，导数始终为正；当x＞0时，函数先增后减再增，即导数先正后负再正，对照选项，应选D.‎ ‎(2)从f′(x)的图象可以看出，在区间内，导数单调递增；在区间内，导数单调递减．即函数f(x)的图象在内越来越陡，在内越来越平缓，由此可知，只有选项D符合．]‎ 9‎ ‎[规律方法]　研究函数与导函数图象之间关系的方法 研究一个函数的图象与其导函数图象之间的关系时，注意抓住各自的关键要素，对于原函数，要注意其图象在哪个区间内单调递增，在哪个区间内单调递减；而对于导函数，则应注意其函数值在哪个区间内大于零，在哪个区间内小于零，并分析这些区间与原函数的单调区间是否一致.‎ ‎[跟踪训练]‎ ‎1．已知y＝xf′(x)的图象如图134所示(其中f′(x)是函数f(x)的导函数)下面四个图象中，y＝f(x)的图象大致是(　　)‎ 图134‎ C　[当0＜x＜1时，xf′(x)＜0，‎ ‎∴f′(x)＜0，故f(x)在(0,1)上为减函数；‎ 当x＞1时，xf′(x)＞0，∴f′(x)＞0，‎ 故y＝f(x)在(1，＋∞)上为增函数．故选C.]‎ 利用导数求函数的单调区间 角度1　不含参数的函数求单调区间 ‎　求下列函数的单调区间．‎ ‎(1)f(x)＝3x2－2ln x；(2)f(x)＝x2·e－x；‎ ‎(3)f(x)＝x＋. ‎ 9‎ ‎【导学号：31062037】‎ ‎[解]　(1)函数的定义域为D＝(0，＋∞)．∵f′(x)＝6x－，令f′(x)＝0，得x1＝，x2＝－(舍去)，用x1分割定义域D，得下表：‎ x f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ ‎∴函数f(x)的单调递减区间为，单调递增区间为.‎ ‎(2)函数的定义域为D＝(－∞，＋∞)．∵f′(x)＝(x2)′e－x＋x2(e－x)′＝2xe－x－x2e－x＝e－x(2x－x2)，令f′(x)＝0，由于e－x＞0，∴x1＝0，x2＝2，用x1，x2分割定义域D，得下表：‎ x ‎(－∞，0)‎ ‎0‎ ‎(0,2)‎ ‎2‎ ‎(2，＋∞)‎ f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ ‎0‎ ‎－‎ f′(x)‎ ‎∴f(x)的单调递减区间为(－∞，0)和(2，＋∞)，单调递增区间为(0,2)．‎ ‎(3)函数的定义域为D＝(－∞，0)∪(0，＋∞)．‎ ‎∵f′(x)＝1－，令f′(x)＝0，得x1＝－1，x2＝1，用x1，x2分割定义域D，得下表：‎ x ‎(－∞，－1)‎ ‎－1‎ ‎(－1,0)‎ ‎(0,1)‎ ‎1‎ ‎(1，＋∞)‎ f′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ ‎∴函数f(x)的单调递减区间为(－1,0)和(0,1)，单调递增区间为(－∞，－1)和(1，＋∞)．‎ 角度2　含参数的函数的单调区间 ‎　讨论函数f(x)＝ax2＋x－(a＋1)ln x(a≥0)的单调性．‎ ‎[思路探究]　―→―→ ‎[解]　函数f(x)的定义域为(0，＋∞)，f′(x)＝ax＋1－ ‎＝.‎ 9‎ ‎(1)当a＝0时，f′(x)＝，‎ 由f′(x)＞0，得x＞1，‎ 由f′(x)＜0，得0＜x＜1.‎ ‎∴f(x)在(0,1)内为减函数，在(1，＋∞)内为增函数．‎ ‎(2)当a＞0时，‎ f′(x)＝，‎ ‎∵a＞0，∴－＜0.‎ 由f′(x)＞0，得x＞1，‎ 由f′(x)＜0，得0＜x＜1.‎ ‎∴f(x)在(0,1)内为减函数，在(1，＋∞)内为增函数．‎ 综上所述，当a≥0时，f(x)在(0,1)内为减函数，在(1，＋∞)内为增函数. ‎ ‎[规律方法]　利用导数求函数单调区间的步骤 ‎(1)确定函数f(x)的定义域．‎ ‎(2)求导数f′(x)．‎ ‎(3)由f′(x)>0(或f′(x)<0)，解出相应的x的范围．当f′(x)>0时，f(x)在相应的区间上是增函数；当f′(x)<0时，f(x)在相应区间上是减函数．‎ ‎(4)结合定义域写出单调区间．‎ ‎[跟踪训练]‎ ‎2．设f(x)＝ex－ax－2，求f(x)的单调区间. ‎ ‎【导学号：31062038】‎ ‎[解]　f(x)的定义域为 ‎(－∞，＋∞)，f′(x)＝ex－a.‎ 若a≤0，则f′(x)＞0，‎ 所以f(x)在(－∞， ＋∞)上单调递增．‎ 若a＞0，则当x∈(－∞，ln a)时，f′(x)＜0；‎ 当x∈(ln a，＋∞)时，f′(x)＞0.‎ 所以f(x)在(－∞，ln a)上单调递减，在(ln a，＋∞)上单调递增．‎ 综上所述，当a≤0时，函数f(x)在(－∞，＋∞)上单调递增；‎ 当a＞0时，f(x)在(－∞，ln a)上单调递减，在(ln a，＋∞)上单调递增.‎ 已知函数的单调性求参数的范围 ‎[探究问题]‎ 9‎ ‎1．在区间(a，b)内，若f′(x)＞0，则f(x)在此区间上单调递增，反之也成立吗？‎ 提示：不一定成立．比如y＝x3在R上为增函数，但其在x＝0处的导数等于零．也就是说f′(x)＞0是y＝f(x)在某个区间上单调递增的充分不必要条件．‎ ‎2．若函数f(x)为可导函数，且在区间(a，b)上是单调递增(或递减)函数，则f′(x)满足什么条件？‎ 提示：f′(x)≥0(或f′(x)≤0)．‎ ‎　已知函数f(x)＝x3－ax－1为单调递增函数，求实数a的取值范围．‎ ‎[思路探究]　―→―→ ‎[解]　由已知得f′(x)＝3x2－a，‎ 因为f(x)在(－∞，＋∞)上是单调增函数，‎ 所以f′(x)＝3x2－a≥0在(－∞，＋∞)上恒成立，‎ 即a≤3x2对x∈R恒成立，因为3x2≥0，所以只需a≤0.‎ 又因为a＝0时，f′(x)＝3x2≥0，‎ f(x)＝x3－1在R上是增函数，所以a≤0.‎ 母题探究：1.(变条件)若函数f(x)＝x3－ax－1的单调减区间为(－1,1)，求a的取值范围．‎ ‎[解]　由f′(x)＝3x2－a，‎ ‎①当a≤0时，f′(x)≥0，‎ ‎∴f(x)在(－∞，＋∞)上为增函数．‎ ‎②当a＞0时，令3x2－a＝0，得x＝±，‎ 当－＜x＜时，f′(x)＜0.‎ ‎∴f(x)在上为减函数，‎ ‎∴f(x)的单调递减区间为，‎ ‎∴＝1，即a＝3.‎ ‎2．(变条件)若函数f(x)＝x3－ax－1在(－1,1)上单调递减，求a的范围．‎ ‎[解]　由题意可知f′(x)＝3x2－a≤0在(－1,1)上恒成立，‎ ‎∴，即，∴a≥3.‎ 即a的取值范围是[3，＋∞)．‎ ‎3．(变条件)若函数f(x)＝x3－ax－1在(－1,1)上不单调，求a的范围．‎ ‎[解]　∵f(x)＝x3－ax－1，‎ 9‎ ‎∴f′(x)＝3x2－a，‎ 由f′(x)＝0，‎ 得x＝±(a≥0)，‎ ‎∵f(x)在区间(－1,1)上不单调，‎ ‎∴0＜＜1，即0＜a＜3.‎ 故a的取值范围为(0,3)．‎ ‎[规律方法]　1.解答本题注意：可导函数f(x)在(a，b)上单调递增(或单调递减)的充要条件是f′(x)≥0(或f′(x)≤0)在(a，b)上恒成立，且f′(x)在(a，b)的任何子区间内都不恒等于0.‎ ‎2．已知f(x)在区间(a，b)上的单调性，求参数范围的方法 ‎(1)利用集合的包含关系处理f(x)在(a，b)上单调递增(减)的问题，则区间(a，b)是相应单调区间的子集；‎ ‎(2)利用不等式的恒成立处理f(x)在(a，b)上单调递增(减)的问题，则f′(x) ≥0(f′(x)≤0)在(a，b)内恒成立，注意验证等号是否成立．‎ ‎[当 堂 达 标·固 双 基]‎ ‎1．设函数f(x)的图象如图135所示，则导函数f′(x)的图象可能为(　　)‎ 图135‎ C　[∵f(x)在(－∞，1)，(4，＋∞)上是减函数，在(1,4)上为增函数，‎ ‎∴当x＜1或x＞4时，f′(x)＜0；‎ 当1＜x＜4时，f′(x)＞0.故选C.]‎ ‎2．函数f(x)＝(x－3)ex的单调递增区间是(　　)‎ ‎ 【导学号：31062039】‎ A．(－∞，2) B．(0,3) ‎ 9‎ C．(1,4) D．(2，＋∞)‎ D　[∵f′(x)＝ex＋(x－3)ex＝(x－2)ex，‎ 由f′(x)＞0得(x－2)ex＞0，∴x＞2.‎ ‎∴f(x)的单调递增区间为(2，＋∞)．]‎ ‎3．函数y＝x2－ln x的单调递减区间为(　　)‎ A．(－1,1] B．(0,1]‎ C．[1，＋∞) D．(0，＋∞)‎ B　[函数y＝x2－ln x的定义域为(0，＋∞)，y′＝x－＝，令y′≤0，则可得0＜x≤1.]‎ ‎4．若函数f(x)＝x3－ax2－x＋6在(0, 1)内单调递减，则实数a的取值范围是 ‎(　　) 【导学号：31062040】‎ A．[1，＋∞)　　 B．a＝1‎ C．(－∞，1] D．(0,1)‎ A　[∵f′(x)＝3x2－2ax－1，‎ 且f(x)在(0,1)内单调递减，‎ ‎∴不等式3x2－2ax－1≤0在(0,1)内恒成立，‎ ‎∴f′(0)≤0，且f′(1)≤0，∴a≥1.]‎ ‎5．试求函数f(x)＝kx－ln x的单调区间．‎ ‎[解]　函数f(x)＝kx－ln x的定义域为(0，＋∞)，f′(x)＝k－＝.‎ 当k≤0时，kx－1＜0，‎ ‎∴f′(x)＜0，‎ 则f(x)在(0，＋∞)上单调递减．‎ 当k＞0时，由f′(x)＜0，即＜0，‎ 解得0＜x＜；‎ 由f′(x)＞0，即＞0，解得x＞.‎ ‎∴当k＞0时，f(x)的单调递减区间为，单调递增区间为.‎ 综上所述，当k≤0时，f(x)的单调递减区间为(0，＋∞)；‎ 当k＞0时，f(x)的单调递减区间为，单调递增区间为.‎ 9‎