【数学】2019届一轮复习苏教版第2章函数概念与基本初等函数I第10讲学案
第10讲 二次函数与幂函数
考试要求 1.幂函数的概念,函数y=x,y=x2,y=x3,y=,y=x的图象与性质(A级要求);2.二次函数的图象与性质及应用(B级要求).
诊 断 自 测
1.思考辨析(在括号内打“√”或“×”)
(1)函数y=2x是幂函数.( )
(2)当n>0时,幂函数y=xn在(0,+∞)上是增函数.( )
(3)二次函数y=ax2+bx+c(x∈R)不可能是偶函数.( )
(4)二次函数y=ax2+bx+c(x∈[m,n])的最值一定是.( )
解析 (1)由于幂函数的解析式为f(x)=xα,故y=2x不是幂函数,(1)错.
(3)由于当b=0时,y=ax2+bx+c=ax2+c为偶函数,故(3)错.
(4)对称轴x=-,当-小于a或大于b时,最值不是,故(4)错.
答案 (1)× (2)√ (3)× (4)×
2.若幂函数y=(m2-3m+3)xm2-m-2的图象不经过原点,则实数m的值为________.
解析 由解得m=1或2.
经检验m=1或2都适合.
答案 1或2
3.(必修1P47习题9改编)已知f(x)=x2+px+q满足f(1)=f(2)=0,则f(-1)的值是________.
解析 由f(1)=f(2)=0知方程x2+px+q=0的两根分别为1,2,则p=-3,q=2,∴f(x)=x2-3x+2,∴f(-1)=6.
答案 6
4.(2016·全国Ⅲ卷改编)已知a=2,b=3,c=25,则a,b,c的大小关系为________.
解析 因为a=2=4,b=3,c=5又y=x在(0,+∞)上是增函数,所以c>a>b.
答案 c>a>b
5.(2017·北京卷)已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是________.
解析 由题意知,y=1-x,
∵y≥0,x≥0,∴0≤x≤1,
则x2+y2=x2+(1-x)2=2x2-2x+1=2+.
当x=时,x2+y2取最小值,
当x=0或x=1时,x2+y2取最大值1,
∴x2+y2∈.
答案
知 识 梳 理
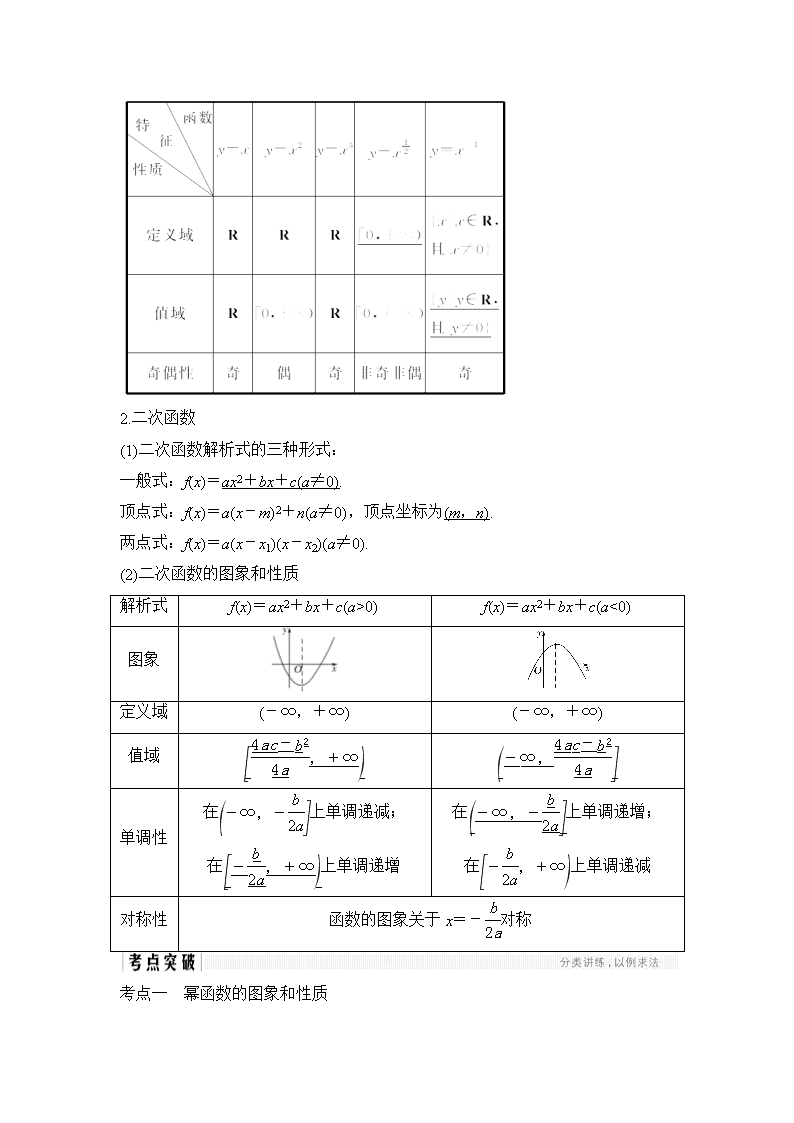
1.幂函数
(1)幂函数的定义
一般地,形如y=xα的函数称为幂函数,其中x是自变量,α为常数.
(2)常见的5种幂函数的图象
(3)常见的5种幂函数的性质
2.二次函数
(1)二次函数解析式的三种形式:
一般式:f(x)=ax2+bx+c(a≠0).
顶点式:f(x)=a(x-m)2+n(a≠0),顶点坐标为(m,n).
两点式:f(x)=a(x-x1)(x-x2)(a≠0).
(2)二次函数的图象和性质
解析式
f(x)=ax2+bx+c(a>0)
f(x)=ax2+bx+c(a<0)
图象
定义域
(-∞,+∞)
(-∞,+∞)
值域
单调性
在上单调递减;
在上单调递增
在上单调递增;
在上单调递减
对称性
函数的图象关于x=-对称
考点一 幂函数的图象和性质
【例1】 (1)(2018·连云港模拟)已知幂函数f(x)=x-,若f(a+1)
>1,
即a0时,图象过原点和(1,1),在第一象限的图象上升;当α<0时,图象不过原点,过(1,1),在第一象限的图象下降.
(3)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,
借助其单调性进行比较,准确掌握各个幂函数的图象和性质是解题的关键.
【训练1】 (1)幂函数y=f(x)的图象过点(4,2),则幂函数y=f(x)的图象是________(填序号).
(2)已知幂函数f(x)=(n2+2n-2)xn2-3n(n∈ )的图象关于y轴对称,且在(0,
+∞)上是减函数,则n的值为________.
解析 (1)设f(x)=xα(α∈R),则4α=2,
∴α=,因此f(x)=x,根据图象的特征,③正确.
(2)∵幂函数f(x)=(n2+2n-2)xn2-3n在(0,+∞)上是减函数,
∴∴n=1,
又n=1时,f(x)=x-2的图象关于y轴对称,故n=1.
答案 (1)③ (2)1
考点二 求二次函数的解析式
【例2】 (1)(2018·南京模拟)已知二次函数f(x)与x轴的两个交点坐标为(0,0)和
(-2,0),且有最小值-1,则f(x)=________.
(2)已知二次函数f(x)的图象经过点(4,3),它在x轴上截得的线段长为2,并且对任意x∈R,都有f(2-x)=f(2+x),则f(x)的解析式为________.
解析 (1)设函数的解析式为f(x)=ax(x+2),
所以f(x)=ax2+2ax,
由=-1,
得a=1,所以f(x)=x2+2x.
(2)∵f(2+x)=f(2-x)对任意x∈R恒成立,
∴f(x)的对称轴为x=2.
又∵f(x)的图象被x轴截得的线段长为2.
∴f(x)=0的两根为1和3.
设f(x)的解析式为f(x)=a(x-1)(x-3)(a≠0),
又f(x)的图象过点(4,3),
∴3a=3,a=1,
∴所求f(x)的解析式为f(x)=(x-1)(x-3),
即f(x)=x2-4x+3.
答案 (1)x2+2x (2)f(x)=x2-4x+3
规律方法 求二次函数解析式的方法
【训练2】 (1)已知二次函数f(x)=ax2+bx+1(a,b∈R),x∈R,若函数f(x)的最小值为f(-1)=0,则f(x)=________.
(2)(2017·南京模拟)若函数f(x)=(x+a)(bx+2a)(常数a,b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式f(x)=________.
解析 (1)设函数f(x)的解析式为f(x)=a(x+1)2=ax2+2ax+a,
由已知f(x)=ax2+bx+1,∴a=1,
故f(x)=x2+2x+1.
(2)由f(x)是偶函数知f(x)图象关于y轴对称,
∴f(x)=bx2+a(b+2)x+2a2为偶函数,则a(b+2)=0,当a=0时,f(x)=bx2,此时它的值域不可能为(-∞,4];
∴当b=-2时,f(x)=-2x2+2a2,
又f(x)的值域为(-∞,4],∴2a2=4,
故f(x)=-2x2+4.
答案 (1)x2+2x+1 (2)-2x2+4
考点三 二次函数的图象与性质(多维探究)
命题角度1 二次函数的单调性
【例3-1】 (1)函数f(x)=ax2+(a-3)x+1在区间[-1,+∞)上是递减的,则实数a的取值范围是________.
(2)若函数f(x)=ax2+(a-3)x+1的单调减区间是[-1,+∞),则a=________.
解析 (1)当a=0时,f(x)=-3x+1在[-1,+∞)上递减,满足条件.
当a≠0时,f(x)的对称轴为x=,
由f(x)在[-1,+∞)上递减知
解得-3≤a<0.综上,a的取值范围为[-3,0].
(2)由题意知a<0,又=-1,∴a=-3.
答案 (1)[-3,0] (2)-3
命题角度2 二次函数的最值
【例3-2】 (1)已知函数f(x)=ax2-2x(0≤x≤1),求函数f(x)的最小值.
(2)已知函数f(x)=x2+ax+3-a,若x∈[-2,2]时,f(x)≥0恒成立,求a的取值范围.
解 (1)①当a=0时,f(x)=-2x在[0,1]上单调递减,
∴f(x)min=f(1)=-2.
②当a>0时,f(x)=ax2-2x的图象开口向上,
且对称轴为x=.
(ⅰ)当0<≤1,即a≥1时,
f(x)=ax2-2x的对称轴在[0,1]内,
∴f(x)在上单调递减,在上单调递增.
∴f(x)min=f =-=-.
(ⅱ)当>1,即04时,g(a)=f(-2)=7-3a≥0,得a≤,故此时a不存在.
②当-∈[-2,2],即-4≤a≤4时,g(a)=f =3-a-≥0,得-6≤a≤2,又-4≤a≤4,
故-4≤a≤2.
③当->2,即a<-4时,g(a)=f(2)=7+a≥0,
得a≥-7,又a<-4,故-7≤a<-4,
综上得-7≤a≤2.
命题角度3 二次函数的图象及应用
【例3-3】 (2016·全国Ⅱ卷改编)已知函数f(x)(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3|与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则xi=________.
解析 由f(x)=f(2-x)知函数f(x)的图象关于直线x=1对称.又y=|x2-2x-3|=
|(x-1)2-4|的图象也关于直线x=1对称,所以这两函数的交点也关于直线x=1对称.
不妨设x1>2a.
答案 (0.2)a>>2a
5.若函数f(x)=x2-a|x-1|在[0,+∞)上递增,则实数a的取值范围是________.
解析 f(x)=
x∈[1,+∞)时,f(x)=x2-ax+a=+a-,
x∈(-∞,1)时,f(x)=x2+ax-a=-a-.
①当>1,即a>2时,f(x)在上是递减的,在上是递增的,不合题意;
②当0≤≤1,即0≤a≤2时,符合题意;
③当<0,即a<0时,不符合题意.
综上,a的取值范围是[0,2].
答案 [0,2]
6.(2018·如东高级中 期中)已知a为正实数,函数f(x)=x2-2x+a,且对任意的x∈[0,a],都有f(x)∈[-a,a],则实数a的取值范围为________.
解析 当00,b∈R,c∈R).
(1)若函数f(x)的最小值是f(-1)=0,且c=1,
F(x)=求F(2)+F(-2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
解 (1)由已知c=1,a-b+c=0,且-=-1,
解得a=1,b=2,
∴f(x)=(x+1)2.
∴F(x)=
∴F(2)+F(-2)=(2+1)2+[-(-2+1)2]=8.
(2)由a=1,c=0,得f(x)=x2+bx,
从而|f(x)|≤1在区间(0,1]上恒成立等价于-1≤x2+bx≤1在区间(0,1]上恒成立,
即b≤-x且b≥--x在(0,1]上恒成立.
又-x的最小值为0,--x的最大值为-2.
∴-2≤b≤0.
故b的取值范围是[-2,0].
二、选做题
11.(2015·四川卷改编)如果函数f(x)=(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间上单调递减,那么mn的最大值为________.
解析 当m=2时,f(x)=(n-8)x+1在区间上单调递减,则n-8<0⇒n<8,于是mn<16,则mn无最大值.当m∈[0,2)时,f(x)的图象开口向下且过点(0,1),要使f(x)在区间上单调递减,需-≤,即2n+m≤18,又n≥0,则mn≤m=-m2+9m.而g(m)=-m2+9m在区间[0,2)上为增函数,∴m∈[0,2)时,g(m)2时,f(x)的图象开口向上且过点(0,1),要使f(x)在区间上单调递减,需-≥2,即2m+n≤12,而2m+n≥2,所以mn≤18,当且仅当即时,取“=”,
此时满足m>2.故(mn)max=18.
综上可得,(mn)max=18.
答案 18
12.(2016·浙江卷)已知a≥3,函数F(x)=min{2|x-1|,x2-2ax+4a-2},其中min{p,q}=
(1)求使得等式F(x)=x2-2ax+4a-2成立的x的取值范围;
(2)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
解 (1)由于a≥3,故当x≤1时,(x2-2ax+4a-2)-2|x-1|=x2+2(a-1)(2-x)>0,
当x>1时,(x2-2ax+4a-2)-2|x-1|=(x-2)(x-2a).
所以使得等式F(x)=x2-2ax+4a-2成立的x的取值范围是[2,2a].
(2)(ⅰ)设函数f(x)=2|x-1|,g(x)=x2-2ax+4a-2,则f(x)min=f(1)=0,g(x)min=g(a)=-a2+4a-2,
所以由F(x)的定义知m(a)=min,
即m(a)=
(ⅱ)当0≤x≤2时,F(x)=f(x)≤max=2=F(2).
当2≤x≤6时,F(x)=g(x)≤max
=max=max.
所以,M(a)=