- 2021-04-16 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版九年级数学(下册)第三章圆
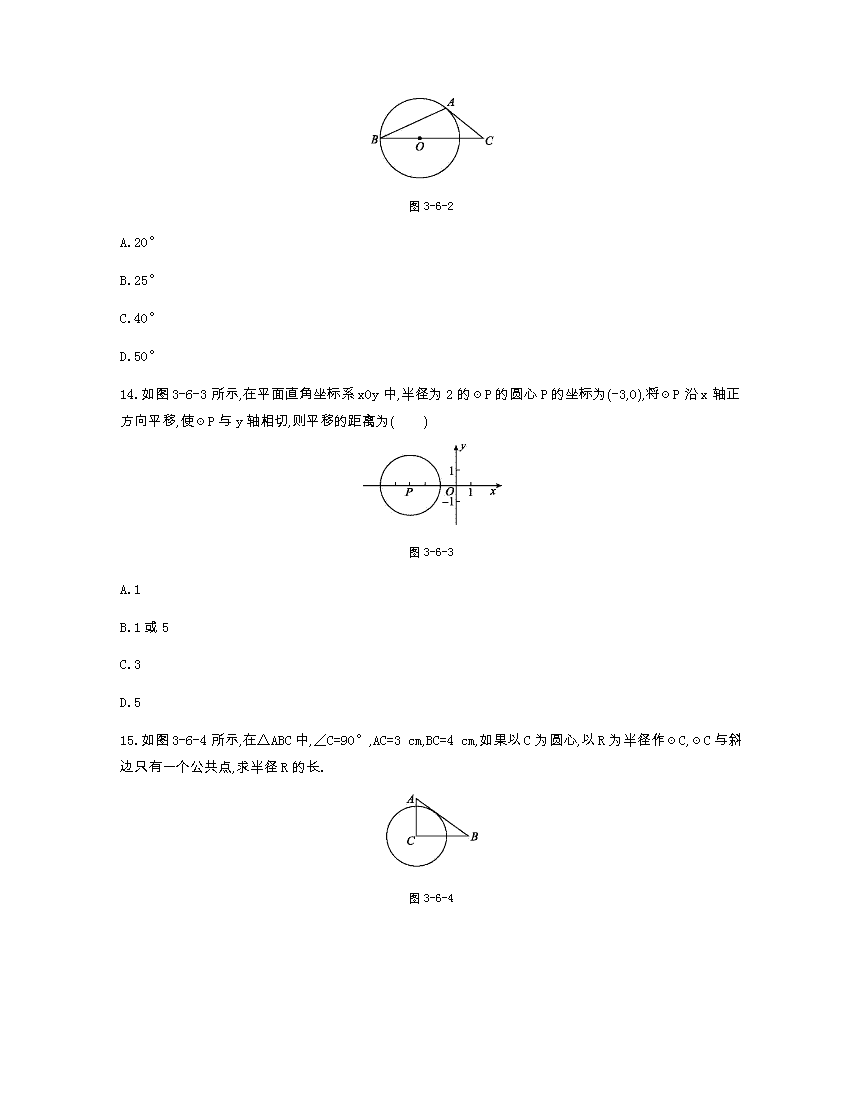
北师大版九年级数学(下册) 第三章 圆 3.6直线和圆的位置关系 课时练习 1.一条直线与一个圆有两个公共点,叫做这条直线与这个圆 . 2.一条直线与一个圆只有一个公共点,叫做这条直线与这个圆 ,这条直线叫做圆的 ,这个唯一的公共点叫做 . 3.一条直线与一个圆没有公共点,叫做这条直线与这个圆 . 4.设圆的半径为r,圆心到直线的距离为d,则: 直线和圆相交时,d r; 直线和圆相切时,d r; 直线和圆相离时,d r. 5.圆的切线垂直于过 的半径. 6.若直线l上一点到圆心的距离等于☉O的半径,则l与☉O的位置关系是( ) A.相交 B.相交或相切 C.相切 D.相离 7.已知☉O的半径为5,直线l上有一点P满足PO=5,则直线l与☉O的位置关系是( ) A.相切 B.相离 C.相离或相切 D.相切或相交 8.如图3-6-1所示,PA切☉O于点A,若∠APO=30°,OP=2,则☉O的半径是( ) 图3-6-1 A. B.1 C.2 D.4 9.已知☉O的半径为5 cm,O到直线l的距离为d,当d=4 cm时,直线l与☉O ;当d= 时,直线l与☉O相切;当d=6 cm时,直线l与☉O . 10.已知圆的直径等于30 cm,直线l与圆只有一个公共点,则圆心到直线l的距离是 cm. 11.已知圆的直径为13 cm,如果直线和圆心的距离为4.5 cm,那么直线和圆有 个公共点. 12.已知☉O的半径为5,直线l是☉O的切线,则点O到直线l的距离是( ) A.2.5 B.3 C.5 D.10 13.如图3-6-2所示,AB是☉O的弦,AC是☉O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于( ) 图3-6-2 A.20° B.25° C.40° D.50° 14.如图3-6-3所示,在平面直角坐标系xOy中,半径为2的☉P的圆心P的坐标为(-3,0),将☉P沿x轴正方向平移,使☉P与y轴相切,则平移的距离为( ) 图3-6-3 A.1 B.1或5 C.3 D.5 15.如图3-6-4所示,在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,如果以C为圆心,以R为半径作☉C,☉C与斜边只有一个公共点,求半径R的长. 图3-6-4 16.设圆的半径为r,圆心到直线的距离为d,则直线与圆相切⇔d r. 17.切线的判定: (1)过半径外端且 半径的直线是圆的切线. (2)如果圆心到一条直线的距离等于 ,那么这条直线是圆的切线. 18.三角形的内切圆: (1)和三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心是三角形 的交点,叫做三角形的 . (2)三角形的内心到三角形 的距离相等. 19.下列直线中,一定是圆的切线的是( ) A.与圆有公共点的直线 B.垂直于圆的半径的直线 C.与圆心的距离等于半径的直线 D.经过圆的直径一端的直线 20.三角形的内心是( ) A.三条边的中线的交点 B.三条角平分线的交点 C.三条边的垂直平分线的交点 D.三边的三条高的交点 21.如图3-6-5所示,AB是☉O的直径,点C在AB的延长线上,CD与☉O相切于点D,若∠C=20°,则∠CDA= . 图3-6-5 22.如图3-6-6所示,A,B是☉O上两点,AC是过A点的一条直线.若∠AOB=120°,则当∠CAB等 于 时,AC才能成为☉O的切线. 图3-6-6 23.如图3-6-7所示,直线AD经过直径AB的一端点A,C为☉O上一点,且∠CAD=∠CBA,则直线AD是☉O的 . 图3-6-7 24.如图3-6-8所示,在☉O中,AB是直径,过B点作☉O的切线BC,连接CO,若AD∥OC交☉O于点D.求证:CD是☉O的切线. 图3-6-8 参考答案 1.相交 2.相切 切线 切点 3.相离 4.< = > 5.切点 6.B 7.D 8.B 9.相交 5 cm 相离 10.15 11.2 12.C 13.C 14.B 15.解:如图,设☉C与AB相切于点D,即R=CD. 由AC=3 cm,BC=4 cm, 得AB==5(cm), 故AB·CD=AC·BC, ∴CD===2.4(cm), 即R=2.4 cm. 16.= 17.(1)垂直于 (2)半径 18.(1)相切 三条角平分线 内心 (2)三边 19.C 20.B 21.125° 22.60° 23.切线 24.证明:连接OD. ∵AD∥OC, ∴∠COB=∠A,∠COD=∠ODA. ∵OA=OD, ∴∠ODA=∠OAD. ∴∠COB=∠COD. ∵CO为公共边,OD=OB, ∴△COB≌△COD. ∴∠OBC=∠ODC. ∵BC是☉O的切线,AB是直径, ∴∠OBC=90°,∴∠ODC=90°, ∴CD是☉O的切线.查看更多