湘教版（2012）初中数学八年级下册 2平行四边形的判定（2）导学案

湘教版（2012）初中数学八年级下册 2平行四边形的判定（2）导学案

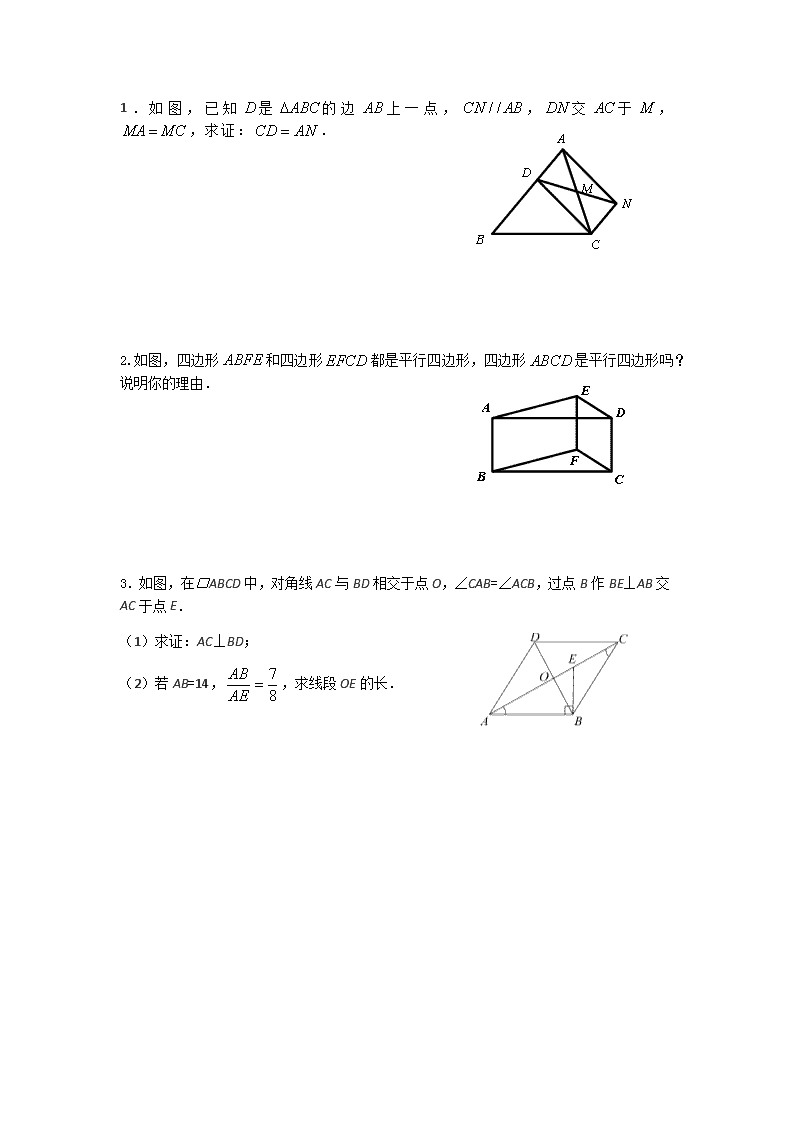
平行四边形的判定（2）导学案 学习目标： 1.会证明平行四边形的判定定理。 2.熟悉平行四边形的判定，并能初步利用平行四边形的判定来解决简单问题。 3.能灵活选择平行四边形的四种判定定理判定一个四边形是否是平行四边形。 学习重点：理解掌握“对角线互相平分的四边形是平行四边形，两组对角分别相等的四边形 是平行四边形”这一判定定理。 学习难点：判定定理的证明方法及运用。 一、学习导入 上节课我们学到的平行四边形的判定方法有： （1） （2） （3） 二、自主探究 探究一：学完“平行四边形的性质和上节课的关于平行四边形的三种判定方法”后，甲同学 结合下图就如何判定一个四边形 ABCD 是平行四边形，还提出了自己的看法，把你帮他进 行证明. 证一证：若 OA=O ,C OD，OB 则四边形 ABCD 是平行四边形. 平行四边形判定方法 4：___________________________________ 几何语言表示：__________________________________ 探究二：若是两组对角分别相等的四边形，是不是平行四边形？ 证一证：在四边形 ABCD 中，∠A =∠C ∠B=∠D。 求证：四边形 ABCD 是平行四边形 平行四边形判定方法 5：___________________________________ 几何语言表示：__________________________________ 总结：本堂课所学的平行四边形判定方法： （1）_______________________________________________________ （2）_______________________________________________________ 三、活学活用 1.关于四边形 ABCD ，①两组对边分别平行；②两组对边分别相等；③有一组对边平行且 相等；④对角线 AC 和 BD 相等；⑤一组对边相等，另一组对边平行；以上五个条件中可 以判定四边形 ABCD 是平行四边形的有（ ） A.1 个 B.2 个 C.3 个 D.4 个 2.下列条件中，不能判定四边形 ABCD 是平行四边形的是（ ） A、∠A=∠C，∠B=∠D B、∠A=∠B=∠C=90° C、∠A+∠B=180 ° ，∠B+∠C=180° D、∠A+∠B=180° ，∠C+∠D=180° 3.如图，在平行 四边形 ABCD 中，对角线 AC 和 BD 相交于点 O ，已知点 ,E F 分别 为 ,OA OC 的中点，证明：四边形 BFDE 是平行四边形. 四、技能提升 1．如图，已知 D 是 ABC 的边 AB 上一点， / /CN AB ，DN 交 AC 于 M ，MA MC ， 求证： CD AN ． 2.如图，四边形 ABFE 和四边形 EFCD 都是平行四边形，四边形 ABCD 是平行四边形吗？ 说明你的理由． 3. 如图，在□ABCD 中，对角线 AC 与 BD 相交于点 O，∠CAB=∠ACB，过点 B 作 BE⊥AB 交 AC 于点 E． （1）求证：AC⊥BD； （2）若 AB=14， 8 7 AE AB ，求线段 OE 的长．