- 2021-04-15 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考复习利用轴对称性质求几何最值
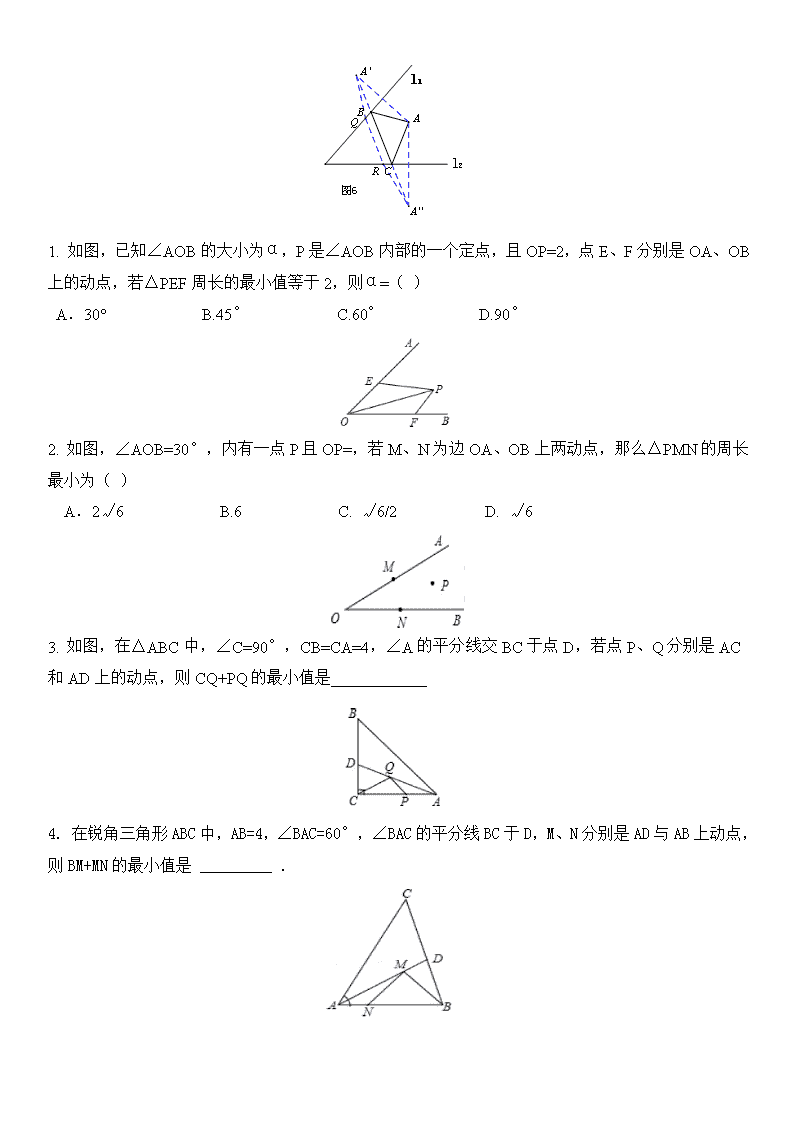
轴对称中几何动点最值问题总结 轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形” 中,为应用某些基本定理提供方便。比如我们可以利用轴对称性质求几何图形中一些线段和的最大值 或最小值问题。 利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个: (1)两点之间线段最短; (2)三角形两边之和大于第三边; (3)垂线段最短。 初中阶段利用轴对称性质求最值的题目可以归结为:两点一线,两点两线,一点两线三类线段和的 最值问题。下面对三类线段和的最值问题进行分析、讨论。 (1) 两点一线的最值问题: (两个定点 + 一个动点) 问题特征:已知两个定点位于一条直线的同一侧,在直线上求一动点的位置,使动点与定点线段和最 短。 核心思路:这类最值问题所求的线段和中只有一个动点,解决这类题目的方法是找出任一定点关于直 线的对称点,连结这个对称点与另一定点,交直线于一点,交点即为动点满足最值的位置。 变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、正方 形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。 1. 如图,等边△ABC 的边长为 6,AD 是 BC 边上的中线,M 是 AD 上的动点,E 是 AC 边上一点, 若 AE=2,EM+CM 的最小值为( ) A.4 B.8 C. D. 2. 如图,等边△ABC 的边长为 4,AD 是 BC 边上的中线,F 是 AD 边上的动点,E 是 AC 边上一点,若 AE=2,当 EF+CF 取得最小值时,则∠ECF 的度数为( ) A.15° B.22.5° C.30° D. 45° 3. 如图,Rt△ABC 中,AC=BC=4,点 D,E 分别是 AB,AC 的中点,在 CD 上找一点 P,使 PA+PE 最小, 则这个最小值是 _____________. 4. (2006•河南)如图,在△ABC 中,AC=BC=2,∠ACB=90°,D 是 BC 边的中点,E 是 AB 边上一动点, 则 EC+ED 的最小值是_____________. 5.如图,在正方形 ABCD 中,E 是 AB 上一点,BE=2,AE=3BE,P 是 AC 上一动点,则 PB+PE 的最小值是( ) A. B. C. D. 10 6..(2009•抚顺)如图所示,正方形 ABCD 的面积为 12,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为( ) A.2√3 B. 2√6 C. 3 D. √6 (2) 一点两线的最值问题: (两个动点+一个定点) 问题特征:已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最短。 核心思路:这类问题实际上是两点两线段最值问题的变式,通过做这一定点关于两条线的对称点,实 现“搬点移线”,把线段“移”到同一直线上来解决。 变异类型: 例 1 :如图 6,接力赛场上,甲同学站在 L1、L2 两条交叉跑道之间的任意一点 A 处,要将接力棒传 给站在 L1 跑道上的乙同学,乙同学要将接力棒传给站在 L2 跑道上的丙同学,丙同学跑回 A 处,试 找出乙丙同学所站的最佳位置使比赛的路程最短。 1. 如图,已知∠AOB 的大小为α,P 是∠AOB 内部的一个定点,且 OP=2,点 E、F 分别是 OA、OB 上的动点,若△PEF 周长的最小值等于 2,则α=( ) A.30° B.45° C.60° D.90° 2. 如图,∠AOB=30°,内有一点 P 且 OP=,若 M、N 为边 OA、OB 上两动点,那么△PMN 的周长 最小为( ) A.2√6 B.6 C. √6/2 D. √6 3. 如图,在△ABC 中,∠C=90°,CB=CA=4,∠A 的平分线交 BC 于点 D,若点 P、Q 分别是 AC 和 AD 上的动点,则 CQ+PQ 的最小值是____________ 4. 在锐角三角形 ABC 中,AB=4,∠BAC=60°,∠BAC 的平分线 BC 于 D,M、N 分别是 AD 与 AB 上动点, 则 BM+MN 的最小值是 _________ . l2 l1 图6 C B A' A'' AQ R (3) 两点两线的最值问题: (两个动点+两个定点) 问题特征:两动点,其中一个随另一个动(一个主动,一个从动),并且两动点间的距离保持不变。 核心思路:用平移方法,可把两动点变成一个动点,转化为“两个定点和一个动点”类型来解。 变异类型: 例 1 如图 4,河岸两侧有 、 两个村庄,为了村民出行方便,计划在河上修一座桥,桥修在 何处才能两村村民来往路程最短? 解析:设桥端两动点为 、 ,那么 点随 点而动, 等于河宽,且 垂直于河岸。 将 向上平移河宽长到 ,线段 与河北岸线的交点即为桥端 点位置。四边形 为平行四 边形, ,此时 值最小。那么来往 、 两村最短路程为: 。 2.如图,在直角坐标系中有线段 AB,AB=50cm,A、B 到 x 轴的距离分别为 10cm 和 40cm,B 点到 y 轴的距离 为 30cm,现在在 x 轴、y 轴上分别有动点 P、Q,当四边形 PABQ 的周长最短时,则这个值为( ) A.50 B.50√5 C. 50(√5-1) D. 50(√5-1) 3. (2010 年天津市中考)在平面角坐标系中,矩形 的顶点 在坐标原点,顶点 、 分别 在 轴、 轴的正半轴上, , , 为边 的中点。 (1)若 为边 上的一个动点,当 的周长最小时,求点 的坐标; (2)若 , 为边 上的两个动点,且 ,当四边形 的周长最小时,求点 , 的坐 标。 解析:作点 关于 轴的对称点 ,则 , 。 (1)连接 交 轴于点 ,连接 ,此时 的周长最小。由 可知 , 那么 ,则 。 (2)将 向左平移 2 个单位( )到 点,定点 、 分别到动点 、 的距离和等于为定点 、 到动点 的距离和,即 。从而把“两个定点和两个动点”类问题转化成“两个定点和一个 动点”类型。 在 上 截 取 , 连 接 交 轴 于 , 四 边 形 为 平 行 四 边 形 , 。 此 时 值最小,则四边形 的周长最小。由 、 可求直线 解析 式为 ,当 时, ,即 ,则 。(也可以用(1)中相似的方法求 坐标) (4) 两点两线的最值问题: (两个动点+两个定点) 问题特征:两动点分别在两条直线上独立运动,一动点分别到一定点和另一动点的距离和最小。 核心思路:利用轴对称变换,使一动点在另一动点的对称点与定点的线段上(两点之间线段最短), 且这条线段垂直于另一动点的对称点所在直线(连接直线外一点与直线上各点的所有线段中,垂线段 最短)时,两线段和最小,最小值等于这条垂线段的长。 变异类型:演变为多边形周长、折线段等最值问题。 例 5 (2009 年陕西省中考)如图 6,在锐角 中, , , 的平分线交 于点 , 、 分别是 和 上的动点,则 的最小值为 4 。 解析:角平分线所在直线是角的对称轴, 上动点 关于 的对称点 在 上, , ,当 时, 最小。 作 于 ,交 于 , ∵ , ∴ 作 交 于 , 2:如图 9,在矩形 ABCD 中,AB=20cm,BC=10cm,在 AC,AB 上各取一点 M,N,使 BM+MN 的值最小,求 这个最小值。 分析:在△ABC 中,AB=20cm,BC=10cm,由勾股定理得 AC==10 cm,由 AC×BO=AB×BC,得 BO=4 cm,所以 BB’=8 cm。 由△ABC∽△B’NB,得 B’N=16cm ,即 BM+MN 的最小值为 16cm 。 3 :如图 5,∠MON=30°,边 OM、ON 分别有定点 A、D,OA=2,OD=5,在 ON、OM 边上确定动点 B、C 的位 置,使折线 ABCD 的长度最短,这时折线 ABCD 的长度为() 分析:若 A 位于 ON 的另一侧,D 位于 OM 的另一侧,则连接 AD 与 OM、ON 边相交可得 B、C 点的位置。可以 想办法在保持线段 AB、CD 长度不变的情况下,将点 A“搬”至 ON 的另一侧,将点 D“搬”至 OM 的另一侧,将 线段 AB、CD“移”至 BC 所在直线来考虑。作 A 关于 ON 的对称点 A’, D 关于 ON 的对称点 D’,连接 A’D’交 ON,OM 于点 B,C,此时折线 ABCD 的长度最短,连接 OA’,OD’,∠A’OB=∠AOB=∠D’OA=30°,故∠ A’OD’=90°,OA’=OA=2,OD’=OD=5,故折线 ABCD 的长度 等 于 A’D’= 。 图9 OM N B' CD BA 5 5 5 29 图5 C B D' A' O N M A D查看更多