高三数学立体几何历年高考题

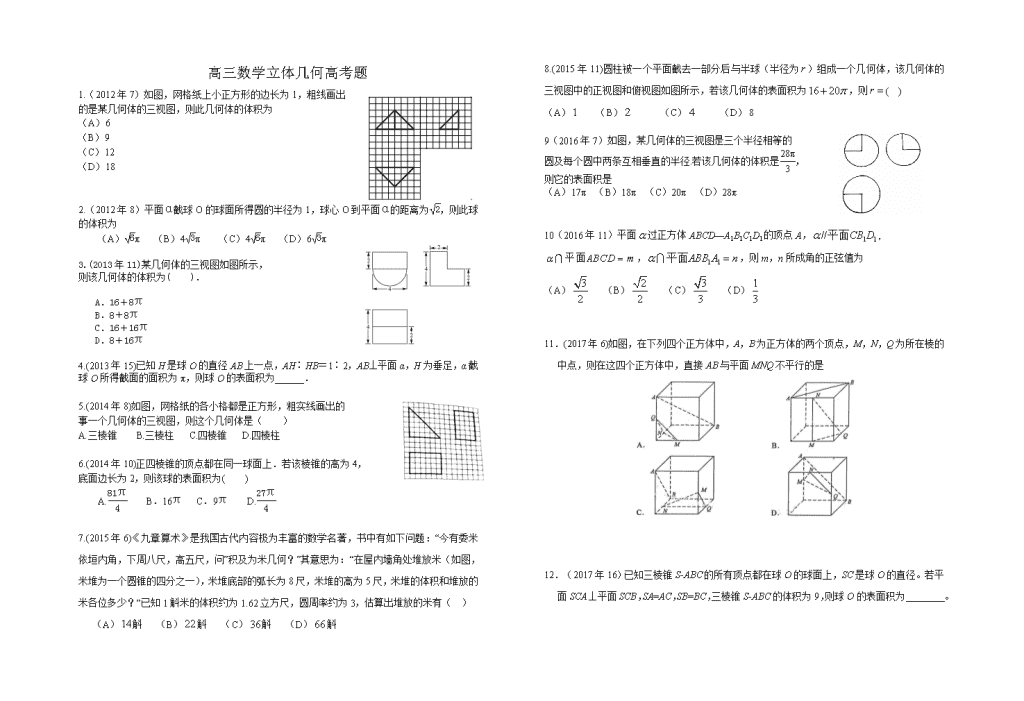
高三数学立体几何历年高考题

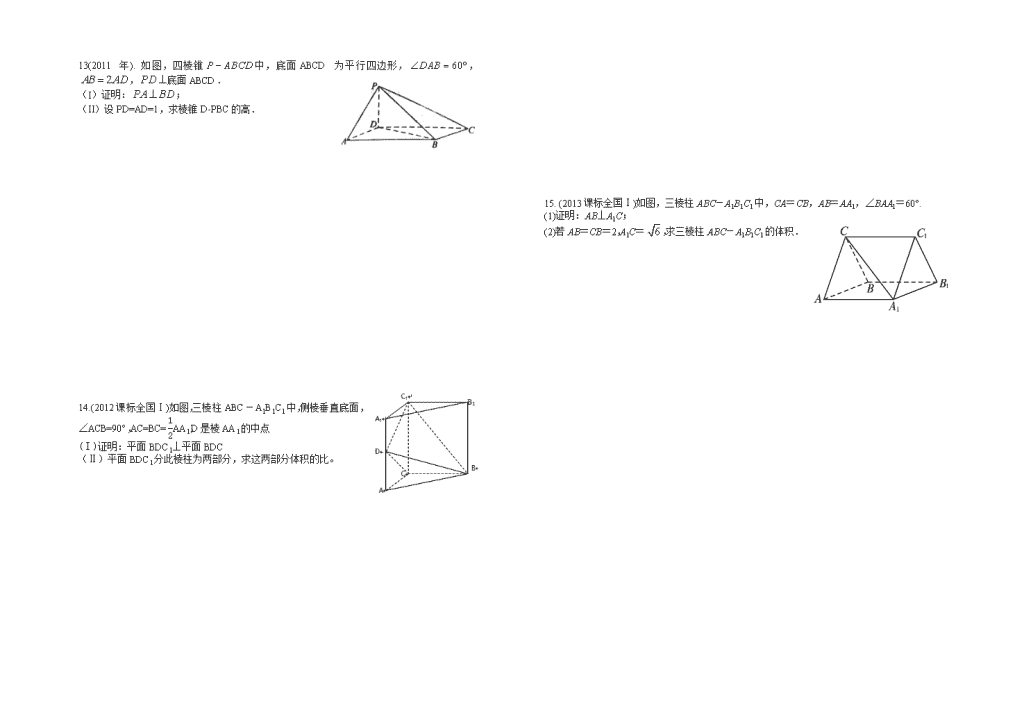
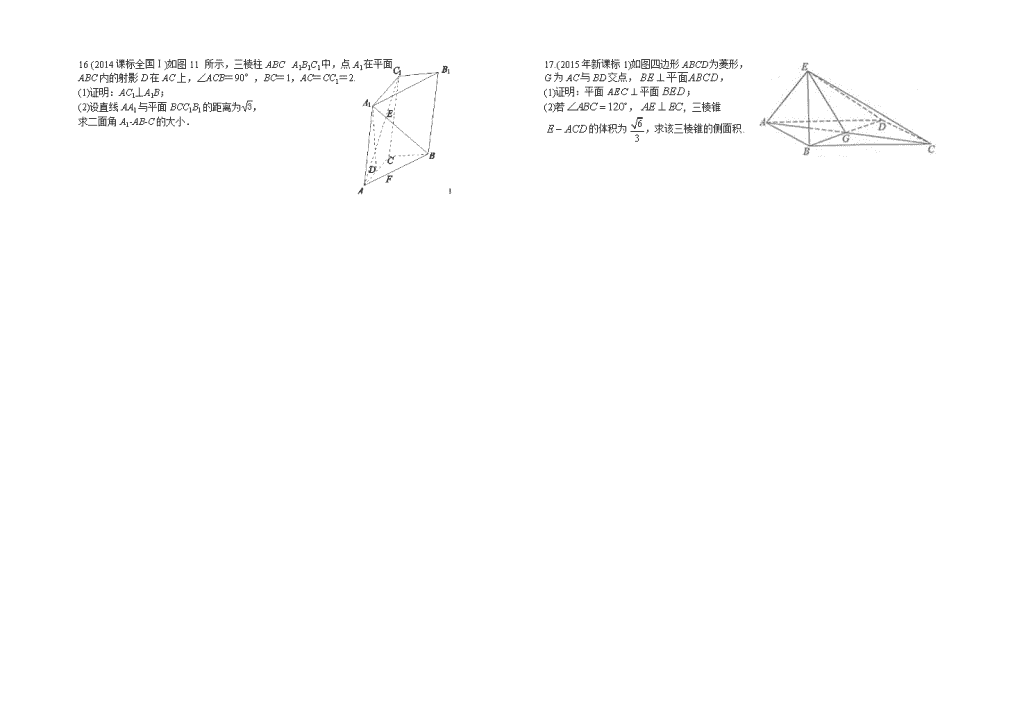
高三数学立体几何高考题 ‎1.（2012年7）如图，网格纸上小正方形的边长为1，粗线画出 的是某几何体的三视图，则此几何体的体积为 ‎（A）6 ‎ ‎（B）9 ‎ ‎（C）12‎ ‎（D）18‎ ‎ ‎ ‎2.（2012年8）平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为 ‎ ‎（A）π （B）4π （C）4π （D）6π ‎3.(2013年11)某几何体的三视图如图所示，‎ 则该几何体的体积为(　　)．‎ A．16＋8π ‎ B．8＋8π C．16＋16π ‎ D．8＋16π ‎4.(2013年15)已知H是球O的直径AB上一点，AH∶HB＝1∶2，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为______．‎ ‎5.(2014年8)如图，网格纸的各小格都是正方形，粗实线画出的 事一个几何体的三视图，则这个几何体是（ ）‎ A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱 ‎ ‎ ‎6.(2014年10)正四棱锥的顶点都在同一球面上．若该棱锥的高为4，‎ 底面边长为2，则该球的表面积为(　　)‎ A. B．16π C．9π D. ‎7.(2015年6)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问”积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各位多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有（ ）‎ ‎（A）斛 （B）斛 （C）斛 （D）斛 ‎8.(2015年11)圆柱被一个平面截去一部分后与半球（半径为）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为，则( )‎ ‎（A） （B） （C） （D）‎ ‎9（2016年7）如图，某几何体的三视图是三个半径相等的 圆及每个圆中两条互相垂直的半径.若该几何体的体积是，‎ 则它的表面积是 ‎（A）17π （B）18π （C）20π （D）28π ‎ ‎10（2016年11）平面过正方体ABCD—A1B1C1D1的顶点A，,‎ ‎，，则m，n所成角的正弦值为 ‎（A） （B） （C） （D）‎ ‎11．(2017年6)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直接AB与平面MNQ不平行的是 ‎12．（2017年16）已知三棱锥S-ABC的所有顶点都在球O的球面上，SC是球O的直径。若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S-ABC的体积为9，则球O的表面积为________。‎ ‎13(2011年).如图，四棱锥中，底面ABCD为平行四边形，，，底面ABCD．‎ ‎（I）证明：；‎ ‎（II）设PD=AD=1，求棱锥D-PBC的高．‎ ‎14.(2012课标全国Ⅰ)如图，三棱柱ABC－A1B‎1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=AA1，D是棱AA1的中点 ‎(Ｉ)证明：平面BDC1⊥平面BDC ‎（Ⅱ）平面BDC1分此棱柱为两部分，求这两部分体积的比。‎ ‎15. (2013课标全国Ⅰ)如图，三棱柱ABC－A1B‎1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.‎ ‎(1)证明：AB⊥A‎1C；‎ ‎(2)若AB＝CB＝2，A‎1C＝，求三棱柱ABC－A1B‎1C1的体积．‎ ‎16 (2014课标全国Ⅰ)如图11所示，三棱柱ABC A1B1C1中，点A1在平面 ABC内的射影D在AC上，∠ACB＝90°，BC＝1，AC＝CC1＝2.‎ ‎(1)证明：AC1⊥A1B；‎ ‎(2)设直线AA1与平面BCC1B1的距离为，‎ 求二面角A1-AB-C的大小．‎ ‎17.(2015年新课标1)如图四边形ABCD为菱形，‎ G为AC与BD交点，，‎ ‎(1)证明：平面平面；‎ ‎(2)若， 三棱锥 的体积为，求该三棱锥的侧面积.‎ ‎18 (2016年新课标1)如图，已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连结PE并延长交AB于点G.‎ ‎（I）证明：G是AB的中点；‎ ‎（II）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．‎ ‎19(2017年新课标1)如图，在四棱锥P-ABCD中，AB//CD，且 ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC,,‎ 且四棱锥P-ABCD的体积为，求该四棱锥的侧面积.‎ 高三数学立体几何高考题答案 ‎1.答案：B ‎2.答案：B ‎3.解析：该几何体为一个半圆柱与一个长方体组成的一个组合体．‎ V半圆柱＝π×22×4＝8π，‎ V长方体＝4×2×2＝16.‎ 所以所求体积为16＋8π.故选A.‎ ‎4.解析：如图，‎ 设球O的半径为R，则AH＝，‎ OH＝.又∵π·EH2＝π，∴EH＝1.‎ ‎∵在Rt△OEH中，R2＝，∴R2＝.∴S球＝4πR2＝.‎ ‎5.答案：B ‎6．A　[解析] 如图所示，因为正四棱锥的底面边长为2，‎ 所以AE＝AC＝.设球心为O，球的半径为R，则OE＝4－R，‎ OA＝R.又因为△AOE为直角三角形，所以OA2＝OE2＋AE2，‎ 即R2＝(4－R)2＋2，解得R＝，‎ 所以该球的表面积S＝4πR2＝4π2＝.‎ ‎7.答案：B ‎8.答案：B ‎9.试题分析：由三视图知：该几何体是个球，设球的半径为，则，‎ 解得，所以它的表面积是，故选A．‎ ‎10试题分析：如图所成角的正弦值为 ‎11.答案：A ‎12答案：‎ ‎13解：（Ⅰ）因为， 由余弦定理得 ‎ 从而BD2+AD2= AB2，故BDAD 又PD底面ABCD，可得BDPD 所以BD平面PAD. 故 PABD ‎（Ⅱ）如图，作DEPB，垂足为E。已知PD底面ABCD，则PDBC。‎ 由（Ⅰ）知BDAD，又BC//AD，所以BCBD。‎ 故BC平面PBD，BCDE。‎ 则DE平面PBC。‎ 由题设知，PD=1，则BD=，PB=2，‎ 根据BE·PB=PD·BD，得DE=，即棱锥D—PBC的高为 ‎14‎ ‎15．1)证明：取AB的中点O，连结OC，OA1，A1B.‎ 因为CA＝CB，所以OC⊥AB.‎ 由于AB＝AA1，∠BAA1＝60°，‎ 故△AA1B为等边三角形，‎ 所以OA1⊥AB.‎ 因为OC∩OA1＝O，所以 AB⊥平面OA‎1C.‎ 又A‎1C⊂平面OA‎1C，故AB⊥A‎1C.‎ ‎(2)解：由题设知△ABC与△AA1B都是边长为2的等边三角形，‎ 所以OC＝OA1＝.‎ 又A‎1C＝，则A‎1C2＝OC2＋，故OA1⊥OC.‎ 因为OC∩AB＝O，所以OA1⊥平面ABC，OA1为三棱柱ABC－A1B‎1C1的高．‎ 又△ABC的面积S△ABC＝，故三棱柱ABC－A1B‎1C1的体积V＝S△ABC×OA1＝3.‎ ‎16．解：方法一：(1)证明：因为A1D⊥平面ABC，A1D⊂平面AA1C1C，‎ 故平面AA1C1C⊥平面ABC.又BC⊥AC，‎ 平面AA1C1C∩平面ABC＝AC，所以BC⊥平面AA1C1C.‎ 连接A1C，因为侧面AA1C1C为菱形，故AC1⊥A1C.‎ 由三垂线定理得AC1⊥A1B.‎ ‎(2)BC⊥平面AA1C1C，BC⊂平面BCC1B1，‎ 故平面AA1C1C⊥平面BCC1B1.‎ 作A1E⊥CC1，E为垂足，则A1E⊥平面BCC1B1.‎ 又直线AA1∥平面BCC1B1，因而A1E为直线AA1与平面BCC1B1的距离，即A1E＝.‎ 因为A1C为∠ACC1的平分线，故A1D＝A1E＝.‎ 作DF⊥AB，F为垂足，连接A1F.由三垂线定理得A1F⊥AB，‎ 故∠A1FD为二面角A1 AB C的平面角．‎ 由AD＝＝1，得D为AC中点，‎ 所以DF＝，tan∠A1FD＝＝，所以cos∠A1FD＝.‎ 所以二面角A1 AB C的大小为arccos.‎ ‎17、解：（I）因为四边形ABCD为菱形，所以AC⊥BD.‎ 因为BE⊥平面ABCD,所以AC⊥BE,故AC⊥平面BED.‎ 又AC平面AEC,所以平面AEC⊥平面BED. ……5分 ‎ ‎（II）设AB=，在菱形ABCD中，又∠ABC= ，可得 AG=GC=，GB=GD=.‎ 因为AE⊥EC,所以在Rt△AEC中，可的EG=.‎ 由BE⊥平面ABCD,知△EBG为直角三角形，可得BE=.‎ 由已知得，三棱锥E-ACD的体积=×AC·GD·BE=.‎ 故=2 ……9分 ‎ 从而可得AE=EC=ED=.‎ 所以△EAC的面积为3，△EAD的面积与 △ECD的面积均为.‎ 故三棱锥E-ACD的侧面积为3+2. ……12分 ‎18试题分析：（1）‎ ‎ ‎ ‎（II）在平面内，过点作的平行线交于点，‎ 即为在平面内的正投影.‎ 理由如下：由已知可得，，又,所以,因此平面，即点为在平面内的正投影.‎ 连结，因为在平面内的正投影为，所以是正三角形的中心.‎ 由（I）知，是的中点，所以在上，故 由题设可得平面，平面，所以，‎ 因此 由已知，正三棱锥的侧面是直角三角形且，可得 ‎ 在等腰直角三角形中，可得 所以四面体的体积 ‎19.【解析】（1）由已知，得,.‎ 由于，故，从而平面.‎ 又平面，所以平面平面.‎ ‎（2）在平面内作，垂足为.‎ 由（1）知，平面，故，可得平面.‎ 设，则由已知可得，.‎ 故四棱锥的体积.‎ 由题设得，故.‎ 从而，，.‎ 可得四棱锥的侧面积为 ‎.‎