七年级下数学课件《互逆命题》 (16)_苏科版

七年级下数学课件《互逆命题》 (16)_苏科版

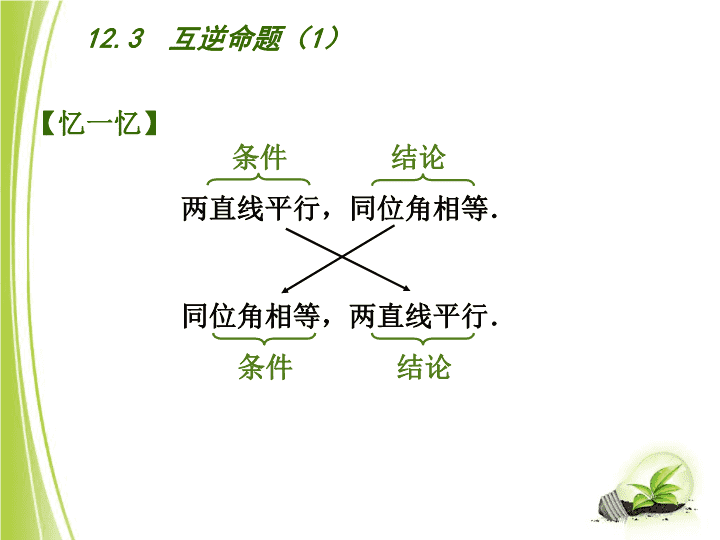
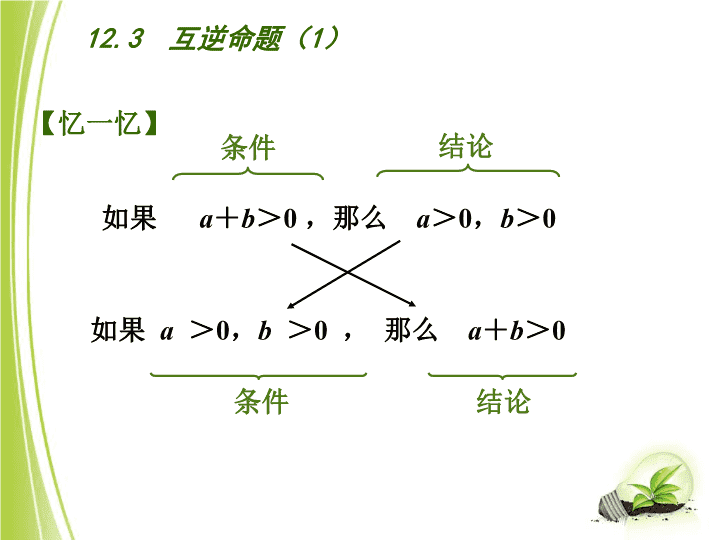
12.3　互逆命题（1） 12.3　互逆命题（1） 两直线平行，同位角相等． 条件 结论 同位角相等，两直线平行． 条件 结论 【忆一忆】 12.3　互逆命题（1） 如果 a＋b＞0 ，那么 a＞0，b＞0 如果 a ＞0，b ＞0 ， 那么 a＋b＞0 【忆一忆】 条件 结论 条件 结论 学习目标 n 1.通过具体实例，了解原命题及其逆命题的概念。 n 2.会识别两个命题是否是互逆命题，并会写出一个命题的逆命题。 n 3.知道原命题成立其逆命题不一定成立。 n 4了解反例的作用，知道利用反例可以证明一个命题是错误的。 学一学 阅读书本第157页试一试以上部分，思考完成下面问题： 1、互逆命题的定义： 两个命题中，如果第一个命题的条件 是 第二个命题的结论，而第一个命题的 又是第二个命题 的 ，那么这两个命题叫做互逆命题. 其中一个命题是 另一个命题 的 . 2、每一个命题都有逆命题吗？为什么？ 3、请你举出一组互逆命题。 知识点一 互逆命题的概念 两个命题中，如果第一个命题的条件是第二个命题 的结论，而第一个命题的结论又是第二个命题的条 件，那么这两个命题叫做互逆命题. 其中一个命题是另一个命题的逆命题. n 知识点二 互逆命题不是指一个命题，而是指两个命题之间的关系； 每一个命题都有逆命题。 　　1．下列各组命题是否是互逆命题： 　　（1）“正方形的四个角都是直角”与“四个 角都是直角的四边形是正方形”； 　　（2）“等于同一个角的两个角相等”与“如 果两个角都等于同一个角，那么这两个角相等”； 　　（3）“对顶角相等”与“如果两个角相等， 那么这两个角是对顶角”； 　　（4）“同位角相等，两直线平行”与“同位 角不相等，两直线不平行” ． 【自我检测一】 2 ．说出下列命题的逆命题，并与同学交流． （1）如果a2＝b2，那么a＝b； （2）如果两个角是对顶角，那么它们的平分线组成一 个平角； （3）末位数字是5的数，能被5整除； （4）锐角与钝角互为补角. 【自我检测一】 逆命题：如果a＝b，那么a2＝b2 . 逆命题：如果两个角的平分线组成一个平角， 那么这两个角是对顶角. 逆命题：能被5整除的数的末位数字是5． 逆命题：互为补角的两个角一个是锐角一个是 钝角． n注意：确定一个命题的逆命题时， 关键是先正确分析命题的条件和结论，然 后交换其位置就可以得到它的逆命题。但 要注意语言的调整，并不是机械的调换， 有时需要把命题写成“如果……那么……” 的形式帮助你写出逆命题。 学一学 阅读书本第158页，思考完成下面问题： 1、一个命题若是真命题需要推理证明，如 果是假命题应如何说明？ 2、说说你对一对互逆命题的真假性的看法， 如果原命题是真命题，它的逆命题一定是 真命题吗？ 自我检测二： 1、见 检测（一）第2题：判断原命题与逆 命题的真假。 2、举反例说明下列命题是假命题： （1）如果|a|＝|b| ，那么a＝b； （2）任何数的平方大于0； （3）两个锐角的和是钝角； （4）如果一点到线段两端的距离相等，那么 这点是这条线段的中点． 注意： 1、原命题与逆命题的真假没有任何联系，即 原命题是真命题，逆命题可能是假命题。真 命题应是公理、定理、定义以及由它们 推导出来的正确的结论。 2、说明一个命题是假命题只需举一个反例， 所谓反例是指举例子符合题中条件的要求， 但不符合题中结论的要求，举反例时要力求 简洁明了。这是数学中常用的方法！ 整理小结： （1）我获得的新知: (2) 我的疑惑 ： 快乐达标： 1.判断下列说法是否正确（正确打“√”，错误打“x”） （1）如果原命题是真命题，那么它的逆命题也是真命题； （ ） （2）如果原命题是假命题，那么它的逆命题也是假命题； （ ） （3）每一个命题都有逆命题； （ ） 2、请写出一个原命题是真命题，逆命题是假命题的 命题： 3、写出下列各命题的逆命题，并判断其逆命题是真命 题还是假命题，若是假命题，请举出一个反例说明。 (1)和为180°的两个角互为补角； (2)相等的角是内错角； (3) 垂直于同一条直线的两条直线平行。 4.如图，现有以下三个论断：①b⊥c， ②a⊥c，③a∥b。请以其中任意两个论 断为条件，第三个论断为结论构造一个 命题，并写出这个命题的逆命题。 a b c 判断你所构造的命题是真命题还是假 命题？ 【小结】： 本节课你学会了什么？你有什么收获？ 必做：课本P161习题12.3 第1（2）、2题. 选做：课本P161习题12.3第2(1)、(3)题 【课后作业】：