- 2021-04-15 发布 |
- 37.5 KB |
- 21页


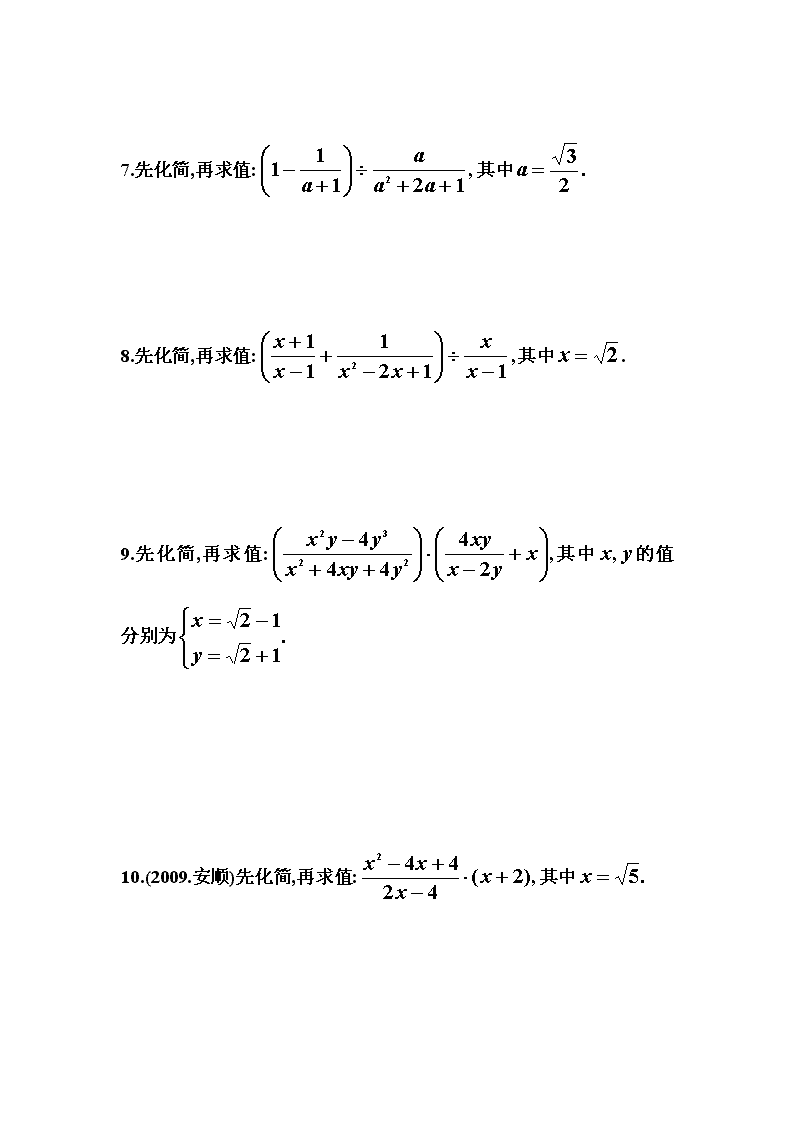
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考化简求值题专项练习及答案
专项辅导(4) 化简求值题及答案 化简求值题在中考数学中占有十分重要的地位,纵观近几年河南省的中考数学试题,都出现了此类题目,所占分值为8分,可见此类题目的重要性!在难度上化简求值题并不难,侧重于对基础知识的考查.进行适当的练习能够对此类题目更好的掌握,在考试中不至于失分! (2008.河南)1.先化简,再求值: 其中. (2009.河南)2.先化简然后从中选取一个合适的数作为的值代入求值. (2010.河南)3.已知将它们组合成 或的形式,请你从中任选一种进行计算,先化 简,再求值,其中 (2011.河南)4.先化简然后从-2≤≤2的范围内选取一个合适的整数作为的值代入求值. (2012.河南)5.先化简然后从<<的范围内选取一个合适的整数作为的值代入求值. 以下题目选取的是九年级上册数学中的化简求值题.请认真完成! 6.先化简,再求值:其中的值分别为 7.先化简,再求值:其中 8.先化简,再求值:其中. 9.先化简,再求值:其中的值分别为 10.(2009.安顺)先化简,再求值:其中 11.(2009.威海)先化简,再求值:其中 12.先化简,再求值:其中(乐山市中考题) 13.先化简然后再选取一个合适的值作为的值代入求值. 14.已知求的值. 15.先化简,再求值:() ÷,其中 是方程x2+3x+1=0的根. 16.(平顶山中考模拟)先化简,再求值:其中小明做这道题时,把抄成计算结果仍正确,请你通过计算说明原因. 17.(2005河南)已知求 18.(2003河南)已知求的值. 19.以后还有总的训练. 2012.11.15 以下为补充题目: 20.(2013.河南) 先化简,再求值:,其中. 21.(2014.河南)先化简,再求值:,其中. 22.(2015.河南)先化简,再求值:,其中, . 23.(2013.许昌一模)先化简,再求值:,然后选择一个你喜欢的数代入求值. 24.(2015.郑州外国语三模)先化简,再求值:,其中 . 25.(2015.郑州外国语月考)先化简,再求值:,其中 . 26.(2015.郑州市九年级一模)先化简,再取恰当的的值代入求值. 27.(2015.郑州市九年级二模)先化简,再从中选一个合适的整数代入求值. 28.(2015.平顶山一模)先化简,再求代数式的值,其中 . 29.(2014.新乡二模)先化简,再求值:,其中是一元二次方程的一个根. 30.(2015.洛阳一模)先化简,再求值:,其中满足. 31.(2014.贺州)先化简,再求值:,其中, . 32.(2014.泰州)先化简,再求值:,其中满足. 33.(2015.湖南岳阳)先化简,再求值:,其中. 34.(2014.苏州)先化简,再求值:,其中. 35.(2015.山东德州)先化简,再求值:,其中. 36.(2014.凉山州)先化简,再求值:,其中满足 37.(2014.宁夏)先化简,再求值:,其中, . 38.(2013.遵义)已知实数满足,求代数式 的值. 39.(2014.泉州)先化简,再求值:,其中. 40.(2013.曲靖改)先化简,再求值:,其中 . 2015.10.6 专项辅导(4) 化简求值题参考答案 ●1.解: 当时 原式 ●2.解: 当时 原式. 注意:这里. ●3.解: 当时 原式 或解: 当时 原式 注意:对于两种选择要注意运算顺序. ●4.解: 当时 原式 或当时 原式 注意:为保证本题中所有分式都有意义,只能取0或. ●5.解: ∵为整数 ∴若使分式有意义,只能取和1 当时 原式 (或当时 原式) ●6.解: 当时 原式 ●7.解: 当时 原式. ●8.解: 当时 原式 ●9.解: ∵ ∴原式 ●10.解: 当时 原式 ●11.解: 当时 原式 ●12.解: 当时 原式 ●13.解: 由题意可知: 当时 原式 ●14.解: ∵ ∴ ∴ ●15.解: ∵是方程的根 ∴ ∴ 原式 注意:对于此类题目,先不要急于解方程,应根据题目化简结果的特点,选择合适的处理方法,如本题可以考虑整体思想采用整体代入的方法. ●16.解: 当时 原式 因为化简结果里面没有,所以本题的计算结果与的取值无关,从而小明在抄错值的情况下所得结果依然正确. ●17.解: 当时 原式 ●18.解: ∴ ∴ ●19.以后还有总的训练. 以下为补充题目: ●20.解: 当时 原式 ●21.解: 当时 原式 ●22.解: 当,时 原式 ●23.解: 当时 原式 注意:本题,. ●24.解: ∵ ∴ ∵ ∴ ∴原式 ●25.解: ∵ ∴原式 ●26.解: ∵ ∴ 当时 原式 ●27.解: ∵ ∴ ∴在中,可取的整数只有2 当时 原式 ●28.解: 当时 原式 ●29.解: ∵是一元二次方程的一个根 ∴ 原式 ●30.解: 解之得: ∵ ∴ 当时 原式 ●31.解: 当,时 原式 ●32.解: ∵ ∴ 原式 ●33.解: 当时 原式 ●34.解: 当时 原式 ●35.解: 当时 原式 ●36.解: ∵ ∴ 原式 ●37.解: 当,时 原式 ●38.解: ∵ ∴ 原式 ●39.解: 当时 原式 ●40.解: 当时 原式 2015.10.6 星期二 15:36查看更多