高中数学必修1教案：第九章直线平面简单几何体(B)(第33课)球(3)

高中数学必修1教案：第九章直线平面简单几何体(B)(第33课)球(3)

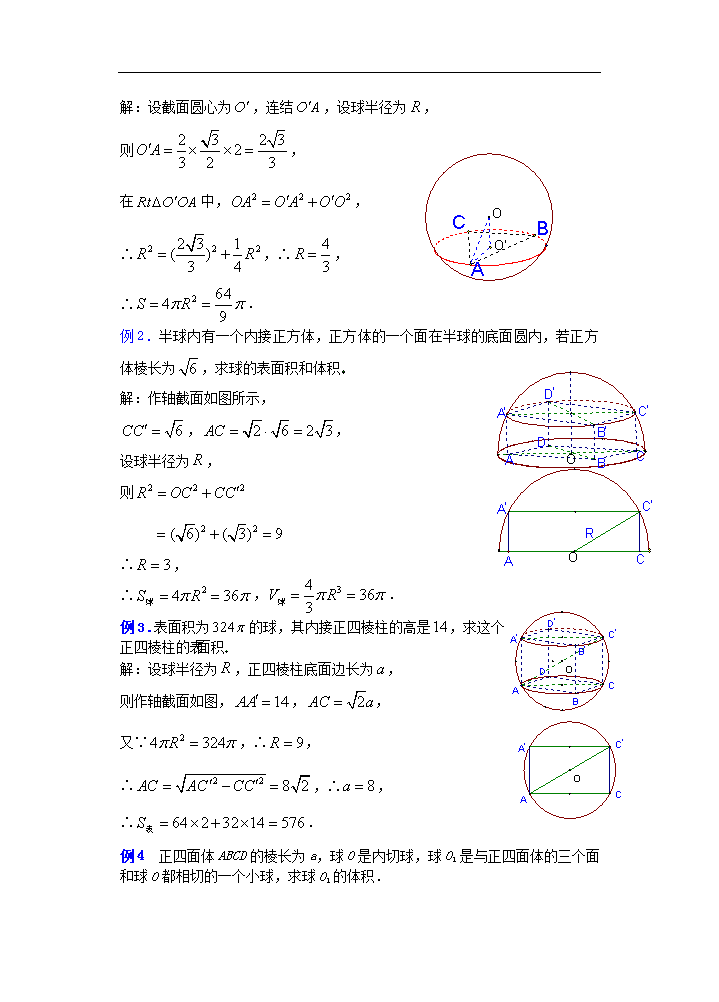
课 题：9．11球(三) ‎ 教学目的：‎ ‎1.了解球的表面积公式的推导过程，体会其基本思想；‎ ‎2.会用球的表面积公式解决有关问题 教学重点：球的表面积公式及其应用 教学难点：球的表面积公式及其应用 授课类型：新授课 ‎ 课时安排：1课时 ‎ 教 具：多媒体、实物投影仪 ‎ 教学过程：‎ 一、复习引入：1 球的概念：‎ ‎ 与定点距离等于或小于定长的点的集合，叫做球体，简称球定点叫球心，定长叫球的半径与定点距离等于定长的点的集合叫做球面一个球或球面用表示它的球心的字母表示，例如球．‎ ‎2．球的截面：‎ 用一平面去截一个球，设是平面的垂线段，为垂足，且，所得的截面是以球心在截面内的射影为圆心，以为半径的一个圆，截面是一个圆面 球面被经过球心的平面截得的圆叫做大圆，被不经过球心的平面截得的圆叫做小圆 ‎3．经度、纬度：‎ 经线：球面上从北极到南极的半个大圆；‎ 纬线：与赤道平面平行的平面截球面所得的小圆；‎ 经度：某地的经度就是经过这点的经线与地轴确定的半平面与经线及轴确定的半平面所成的二面角的度数；‎ 纬度：某地的纬度就是指过这点的球半径与赤道平面所成角的度数 ‎4．两点的球面距离：‎ 球面上两点之间的最短距离，就是经过两点的大圆在这两点间的一段劣弧的长度，我们把这个弧长叫做两点的球面距离 ‎5 半球的底面：‎ ‎ 已知半径为的球，用过球心的平面去截球，球被截面分成大小相等的两个半球，截面圆（包含它内部的点），叫做所得半球的底面 ‎6．球的体积公式：‎ 二、讲解新课：‎ ‎1 球的表面积：‎ 设球的半径为，我们把球面任意分割为一些“小球面片”，它们的面积分别用表示，则球的表面积:‎ 以这些“小球面片”为底，球心为顶点的“小锥体”的体积和等于求的体积，这些“小锥体”可近似地看成棱锥，“小锥体”的底面积可近似地等于“小锥体”的底面积，球的半径近似地等于小棱锥的高，因此，第个小棱锥的体积，当“小锥体”的底面非常小时，“小锥体”的底面几乎是“平的”，于是球的体积:‎ ‎，‎ 又∵，且 ‎∴可得，‎ 又∵，∴，‎ ‎∴即为球的表面积公式 三、讲解范例：‎ 例1 已知过球面上三点的截面和球心的距离为球半径的一半，且，求球的表面积 解：设截面圆心为，连结，设球半径为，‎ 则，‎ 在中，，‎ ‎∴，∴，‎ ‎∴．‎ 例2．半球内有一个内接正方体，正方体的一个面在半球的底面圆内，若正方体棱长为，求球的表面积和体积 解：作轴截面如图所示，‎ ‎，，‎ 设球半径为，‎ 则 ‎ ‎ ‎∴，‎ ‎∴，．‎ 例3．表面积为的球，其内接正四棱柱的高是，求这个正四棱柱的表面积 解：设球半径为，正四棱柱底面边长为，‎ 则作轴截面如图，，，‎ 又∵，∴，‎ ‎∴，∴，‎ ‎∴．‎ 例4 正四面体ABCD的棱长为a，球O是内切球，球O1是与正四面体的三个面和球O都相切的一个小球，求球O1的体积．‎ 分析：正四面体的内切球与各面的切点是面的中心，球心到各面的距离相等．‎ 解：如图，设球O半径为R，球O1的半径为r，E为CD中点，球O与平面ACD、BCD切于点F、G，球O1与平面ACD切于点H．‎ 由题设 ‎　．‎ ‎∵　△AOF∽△AEG ∴　，得．‎ ‎∵　△AO1H∽△AOF ∴ ，得．‎ ‎∴　．‎ 四、课堂练习：‎ ‎1球O1、O2、分别与正方体的各面、各条棱相切，正方体的各顶点都在球O3的表面上，求三个球的表面积之比．‎ 分析：球的表面积之比事实上就是半径之比的平方，故只需找到球半径之间的关系即可．‎ 解：设正方体棱长为a，则三个球的半径依次为、，‎ ‎∴ 三个球的表面积之比是．‎ 五、小结 ：球的表面积公式的推导及应用；球的内接正方体、长方体及外切正方体的有关计算 “分割求近似和化为准确和”‎ 的方法，是一种重要的数学思想方法——极限思想，它是今后要学习的微积分部分“定积分”内容的一个应用；球的体积公式和表面积公式要熟练掌握．‎ 六、课后作业：‎ 七、板书设计（略）‎ 八、课后记：‎