2020_2021学年新教材高中数学第八章立体几何初步8

2020_2021学年新教材高中数学第八章立体几何初步8

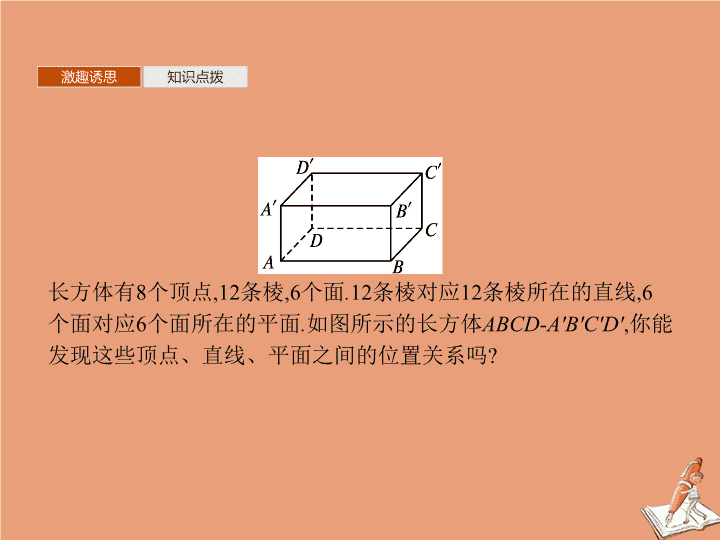
8 . 4 . 2 　 空间点、直线、平面之间的位置关系 课标阐释 思维脉络 1 . 借助长方体 , 了解空间两条直线间的位置关系 . 理解异面直线的定义 . ( 数学抽象、直观想象 ) 2 . 了解直线与平面、平面与平面之间的位置关系 , 并能判断这些位置关系 . ( 逻辑推理 ) 3 . 会用符号语言和图形语言表示直线与直线、直线与平面、平面与平面之间的位置关系 . ( 直观想象、逻辑推理 ) 激趣诱思 知识点拨 长方体有 8 个顶点 ,12 条棱 ,6 个面 . 12 条棱对应 12 条棱所在的直线 ,6 个面对应 6 个面所在的平面 . 如图所示的长方体 ABCD-A'B'C'D' , 你能发现这些顶点、直线、平面之间的位置关系吗 ? 激趣诱思 知识点拨 知识点一、空间中直线与直线的位置 关系 空间两条直线的位置关系有三种 : 微练习 平面内一点与平面外一点连线和这个平面内直线的关系是 　　　　 .  答案 : 相交或异面 激趣诱思 知识点拨 知识点二、空间中直线与平面的位置 关系 激趣诱思 知识点拨 微思考 观察如图所示的长方体 ABCD-A 1 B 1 C 1 D 1 , 线段 A 1 B 所在的直线与长方体的六个面所在平面有几种位置关系 ? 提示 : 直线 A 1 B 在平面 ABB 1 A 1 内 , 与平面 CDD 1 C 1 平行 , 与其余四个面相交 . 激趣诱思 知识点拨 微练习 直线 l 与平面 α 有两个公共点 , 则 ( 　　 ) A. l ∈ α B. l ∥ α C. l 与 α 相交 D. l ⊂ α 答案 : D 激趣诱思 知识点拨 知识点三、空间中平面与平面的位置 关系 激趣诱思 知识点拨 微练习 (1) 正方体的六个面中互相平行的平面有 ( 　　 ) A.1 对　　 B.2 对　　 C.3 对　　 D.4 对 解析 : 如图 , 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , 平面 ABCD ∥ 平面 A 1 B 1 C 1 D 1 , 平面 ABB 1 A 1 ∥ 平面 CDD 1 C 1 , 平面 ADD 1 A 1 ∥ 平面 BCC 1 B 1 , 故六个面中互相平行的平面有 3 对 . 答案 : C 探究一 探究二 探究三 素养形成 当堂检测 空间中两条直线位置关系的判定 例 1 (1) 在正方体 ABCD-A 1 B 1 C 1 D 1 中 , 判断 下列 直线 间的位置关系 : ① 直线 A 1 B 与直线 D 1 C 　　　 ;  ② 直线 A 1 B 与直线 B 1 C 　　　 ;  ③ 直线 D 1 D 与直线 CE ( E 为线段 C 1 D 1 的中点 ) 　　　　 ;  ④ 直线 AB 与直线 B 1 C 　　　　 .  (2) 已知三条直线 a , b , c , a 与 b 异面 , b 与 c 异面 , 则 a 与 c 有什么样的位置关系 ? 请画图说明 . 探究一 探究二 探究三 素养形成 当堂检测 分析 (1 ) (2) 根据异面直线的定义分析 . 探究一 探究二 探究三 素养形成 当堂检测 解 : (1) ① 平行 　 ② 异面 　 ③ 相交 　 ④ 异面 (2) 直线 a 与 c 的位置关系有三种情况 , 如图所示 . 直线 a 与 c 可能平行 , 如图 ① ; 可能相交 , 如图 ② ; 可能异面 , 如图 ③ . 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 空间中两条直线位置关系的判定方法 (1) 判定两条直线平行或相交可用平面几何的方法去判断 . (2) 判定两条直线是异面直线的方法 : ① 定义法 : 由定义判断两直线不可能在同一平面内 ; ② 排除法 ( 反证法 ): 排除两直线共面 ( 平行或相交 ); ③ 重要结论 : 连接平面内一点与平面外一点的直线和这个平面内不经过此点的直线是异面直线 . 如图 , A ∉ α , B ∈ α , l ⊂ α , B ∉ l ⇒ AB 与 l 是异面直线 . 延伸探究 在本例题的正方体中 , 所有与直线 AB 异面的棱所在的直线为 　　　　　 .  答案 : CC 1 , B 1 C 1 , DD 1 , A 1 D 1 探究一 探究二 探究三 素养形成 当堂检测 直线与平面的位置关系 例 2 给出下列四个命题 : ① 若直线 l 平行于平面 α 内的无数条直线 , 则 l ∥ α ; ② 若直线 a 在平面 α 外 , 则 a ∥ α ; ③ 若直线 a ∥ b , 直线 b ⊂ α , 则 a ∥ α , 其中真命题的个数为 ( 　　 ) A.1 B.2 C.3 D.0 分析 判断直线与平面位置关系 , 除了定义法外 , 还可以借助几何体模型 ( 如长方体等 ) 和举反例进行逐项判断 . 解析 : 对于 ① , 直线 l 虽与平面 α 内无数条直线平行 , 但 l 有可能在平面 α 内 , ∴ l 不一定平行于 α . 故 ① 错 . 对于 ② , ∵ 直线 a 在平面 α 外包括两种情形 : a ∥ α , a 与 α 相交 , 故 ② 错 . 对于 ③ , 由直线 a ∥ b , b ⊂ α , 只能说明 a 和 b 无公共点 , 但 a 可能在平面 α 内 , 故 ③ 错 . 答案 : A 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 直线与平面的位置关系有三种 , 即直线在平面内 , 直线与平面相交 , 直线与平面平行 . (1) 判断直线在平面内 , 需找到直线上不同的两点在平面内 , 根据基本事实 2 知直线在平面内 . (2) 判断直线与平面相交 , 据定义只需判定直线与平面有且只有一个公共点 . (3) 判断直线与平面平行 , 可根据定义判断直线与平面没有公共点 , 也可以排除直线与平面相交及直线在平面内两种情况 , 从而判断直线与平面平行 . 探究一 探究二 探究三 素养形成 当堂检测 延伸探究 若直线 a 不平行于平面 α , 则下列结论成立的是 ( 　　 ) A . α 内的所有直线均与 a 异面 B . α 内不存在与 a 平行的直线 C . α 内直线均与 a 相交 D . 直线 a 与平面 α 有公共点 解析 : 由于直线 a 不平行于平面 α , 则 a 在 α 内或 a 与 α 相交 , 故 A 错 ; 当 a ⊂ α 时 , 在平面 α 内存在与 a 平行的直线 , 故 B 错 ; 因为 α 内的直线也可能与 a 平行或异面 , 故 C 错 ; 由线面平行的定义知 D 正确 . 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 平面与平面的位置关系 例 3 给出的下列四个命题中 , 其中正确命题的个数是 ( 　　 ) ① 若平面 α 内有两条直线和平面 β 平行 , 则这两个平面平行 ; ② 若平面 α 内有无数条直线和平面 β 平行 , 则 α 与 β 平行 ; ③ 若平面 α 内 △ ABC 的三个顶点到平面 β 的距离相等 , 则 α 与 β 平行 ; ④ 若两个不重合平面有无数个公共点 , 则这两个平面的位置关系是相交 . A.0 B.1 C.3 D.4 分析 由平面间的位置关系逐一判断 . 探究一 探究二 探究三 素养形成 当堂检测 解析 : 如图甲 , 平面 α 内有无数条直线与 β 平行 , 但 α 与 β 相交 ; 如图乙 , △ ABC 的三个顶点到 β 的距离相等 , 但 α 与 β 相交 . 故 ①②③ 均错 . 不重合的两个平面 , 若它们有公共点 , 则它们有无数个公共点 , 都在它们的交线上 , 故 ④ 正确 . 答案 : B 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 平面与平面的位置关系的判断方法 判断两个平面相交 , 只需找到两个平面的一个公共点 , 就可根据基本事实 3 知 , 两个不重合的平面是相交的 . 判断两个平面平行 , 可根据定义判断两个平面没有公共点 , 也可以排除两个平面相交 , 从而判断两平面平行 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 已知下列说法 : ① 若两个平面 α ∥ β , a ⊂ α , b ⊂ β , 则 a ∥ b ; ② 若两个平面 α ∥ β , a ⊂ α , b ⊂ β , 则 a 与 b 一定不相交 ; ③ 若两个平面 α ∩ β =b , a ⊂ α , 则 a 与 β 一定相交 . 其中正确的是 　　　　　 . ( 将你认为正确的序号都填上 )  解析 : ① 错 , a 与 b 也可能异面 ; ② 对 , ∵ α ∥ β , ∴ α 与 β 无公共点 . 又 ∵ a ⊂ α , b ⊂ β , ∴ a 与 b 无公共点 , 即 a 与 b 一定不相交 ; ③ 错 , a 与 β 也可能平行 . 答案 : ② 探究一 探究二 探究三 素养形成 当堂检测 平面划分空间问题 典例 互不重合的三个平面最多可以把空间分成 　　　　　 部分 .  解析 : 互不重合的三个平面将空间分成五种情形 : 当三个平面互相平行时 , 将空间分成四部分 ; 当两个平面平行 , 第三个平面与它们相交时 , 将空间分成六部分 ; 当三个平面相交于同一条直线时 , 将空间分成六部分 ; 当三个平面相交于三条直线时 , 且三条交线交于同一点时 , 将空间分成八部分 ; 当三个平面相交于三条直线 , 且三条交线互相平行时 , 将空间分成七部分 . 即不重合的三个平面可以将空间分成四部分或六部分或七部分或八部分 . 所以最多将空间分成八部分 . 答案 : 八 方法点睛 平面划分空间问题 , 应根据平面的位置关系进行讨论分析 , 必要时可以借助空间模型来求解 . 探究一 探究二 探究三 素养形成 当堂检测 1 . 直线 a 与直线 b 相交 , 直线 c 与直线 b 相交 , 则直线 a 与直线 c 的位置关系是 ( 　　 ) A. 相交 B. 平行 C. 异面 D. 以上都有可能 解析 : 如图所示 , 在长方体 ABCD-A 1 B 1 C 1 D 1 中 , AB 与 AA 1 相交 , A 1 B 1 与 AA 1 相交 , AB ∥ A 1 B 1 ; 又 AD 与 AA 1 相交 , AB 与 AD 相交 ; 又 A 1 D 1 与 AA 1 相交 , AB 与 A 1 D 1 异面 . 故选 D. 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 2 . 若 a 是平面 α 外的一条直线 , 则直线 a 与平面 α 内的直线的位置关系是 ( 　　 ) A. 平行 B. 相交 C. 异面 D. 平行、相交或异面 解析 : 若 a ∥ α , 则 a 与 α 内的直线平行或异面 ; 若 a 与 α 相交 , 则 a 与 α 内的直线相交或异面 . 答案 : D 探究一 探究二 探究三 素养形成 当堂检测 3 . 如图 , 在长方体 ABCD-A 1 B 1 C 1 D 1 中 , 与 AA 1 异面的棱是 ( 　　 ) A .AB B .BB 1 C .DD 1 D .B 1 C 1 解析 : AA 1 ∥ BB 1 , AA 1 ∥ DD 1 , AA 1 ∩ AB=A , AA 1 与 B 1 C 1 是异面直线 . 答案 : D 4 . 过平面外两点 , 可作 　　　　　 个平面与已知平面平行 .  解析 : 若过两点的直线与已知平面相交 , 则作不出平面与已知平面平行 ; 若过两点的直线与已知平面平行 , 则可作一个平面与已知平面平行 . 答案 : 0 或 1