- 2021-04-15 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018上海市杨浦区2018届中考二模数学试卷含答案
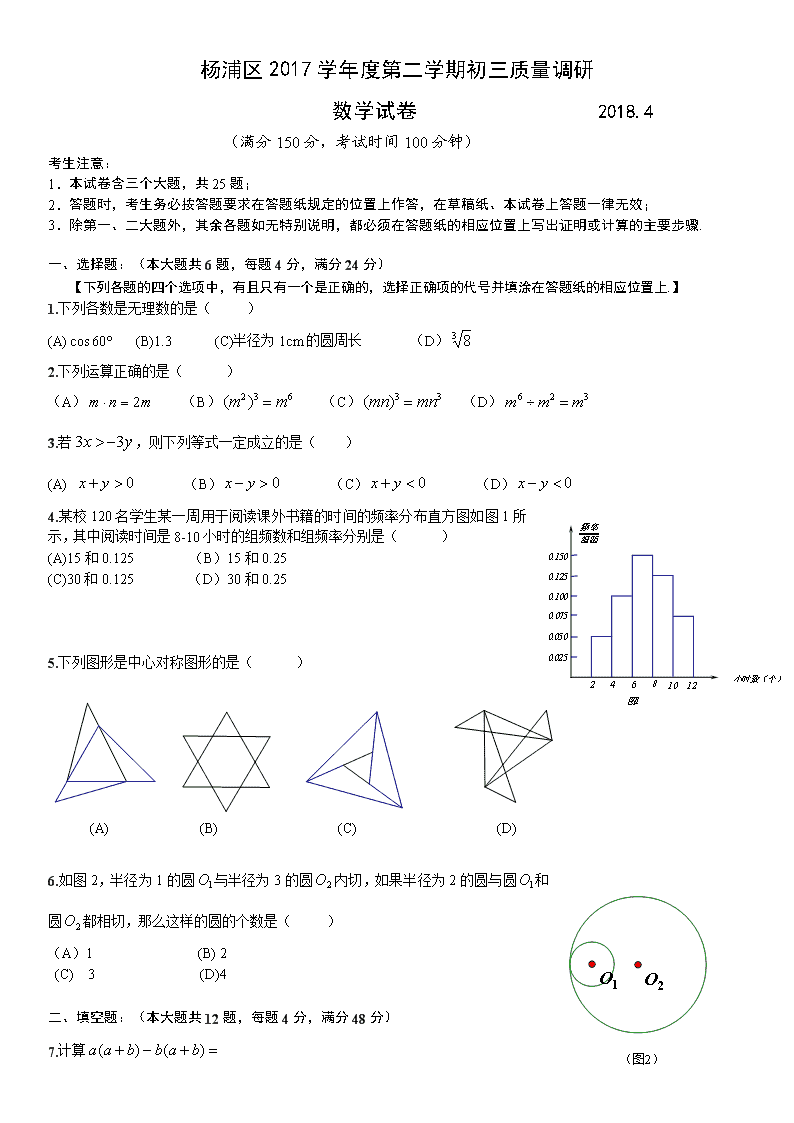
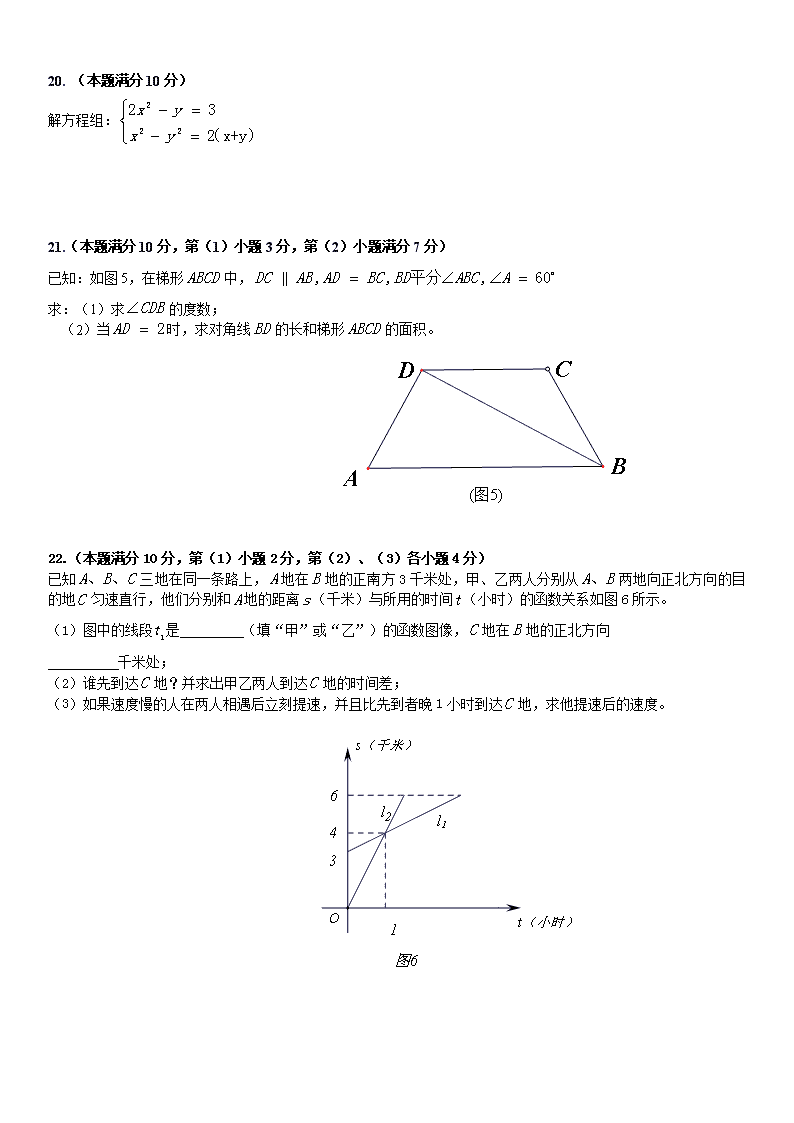
杨浦区2017学年度第二学期初三质量调研 数学试卷 2018.4 (满分150分,考试时间100分钟) 考生注意: 1.本试卷含三个大题,共25题; 2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效; 3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】 1.下列各数是无理数的是( ) (A) (B)1.3 (C)半径为1cm的圆周长 (D) 2.下列运算正确的是( ) (A) (B) (C) (D) 3.若,则下列等式一定成立的是( ) (A) (B) (C) (D) 4.某校120名学生某一周用于阅读课外书籍的时间的频率分布直方图如图1所示,其中阅读时间是8-10小时的组频数和组频率分别是( ) (A)15和0.125 (B)15和0.25 (C)30和0.125 (D)30和0.25 5.下列图形是中心对称图形的是( ) (A) (B) (C) (D) 6.如图2,半径为1的圆与半径为3的圆内切,如果半径为2的圆与圆和圆都相切,那么这样的圆的个数是( ) (A)1 (B) 2 (C) 3 (D)4 二、填空题:(本大题共12题,每题4分,满分48分) 7.计算 8.当时,化简 9. 函数中,自变量取值范围是 10. 如果反比例函数的图像经过点与,那么的值等于 11. 三人中至少两人性别相同的概率是 12. 25位同学10秒钟跳绳的成绩汇总如下表; 人数 1 2 3 4 5 10 次数 15 8 25 10 17 20 那么跳绳的中位数是 13.李明早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时分钟。如 果他骑自行车的平均速度是每分钟米,推车步行的平均速度是每分钟米,他家离学校的路程是米,设他推车步行的时间为分钟,那么可列出的方程是 14.四边形中,向量 15.若正边形的内角为,则边数为 16.如图3,中,,,的垂直平分线交于点,联结.如果,那么的周长为 . 17.如图4,正△的边长为,点、在半径为的圆上,点在圆内,将正绕点逆时针针旋转,当点第一次落在圆上时,旋转角的正切值为 . 18.当关于的一元二次方程有实数根,且其中一个根为另一个根的倍时,称之为“倍根方程”。如果关于的一元二次方程是“倍根方程”,那么的值为 . 三、解答题(本大题共7题,满分78分) 19.(本题满分10分) 先化简,再求值: 20. (本题满分10分) 解方程组: 21.(本题满分10分,第(1)小题3分,第(2)小题满分7分) 已知:如图5,在梯形中, 求:(1)求的度数; (2)当时,求对角线的长和梯形的面积。 22.(本题满分10分,第(1)小题2分,第(2)、(3)各小题4分) 已知三地在同一条路上,地在地的正南方3千米处,甲、乙两人分别从两地向正北方向的目的地匀速直行,他们分别和地的距离(千米)与所用的时间(小时)的函数关系如图6所示。 (1)图中的线段是 (填“甲”或“乙”)的函数图像,地在地的正北方向 千米处; (2)谁先到达地?并求出甲乙两人到达地的时间差; (3)如果速度慢的人在两人相遇后立刻提速,并且比先到者晚1小时到达地,求他提速后的速度。 23.(本题满分12分,第(1)小题6分,第(2)小题6分) 已知:如图7,在中,点为对角线的中点,过点的直线分别交边于点,过点的直线分别交边于点,且. (1)求证:四边形为平行四边形; (2)当四边形为矩形时,求证: . 24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分) 如图8,在平面直角坐标系中,抛物线与轴交于点、,与轴交于点,直线经过点、,点为抛物线上位于直线上方的一个动点. (1) 求抛物线的表达式; (2) 如图(1),当∥时,求的正切值; (3) 当以、为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点的坐标. 25. (本题满分14分,第(1)小题4分,第(2)小题6分,第(3)题4分) 如图9,在梯形中,,,,,点为边上一动点,作⊥,垂足在边上,以点为圆心,为半径画圆,交射线于点。 (1) 当圆过点时,求圆的半径; (2) 分别联结和,当时,以点为圆心,为半径的圆与圆相交,试求圆的半径的取值范围; (3) 将劣弧沿直线翻折交于点,试通过计算说明线段和的比值为定值,并求出次定值。 参考答案: 1、C 2、B 3、A 4、D 5、B 6、C 7、 8、 9、 且 10、 11、1 12、20 13、80x+250(15-x)=2900 14、 15、9 16、14 17、 18、-4或-1 19、 20、 21、(1)30° (2) 22、(1)乙 3 (2)甲 1.5小时 (3)千米每小时 23、略 24、(1) (2) (3) 25、(1)x=3 (2) (3)查看更多