中考数学专题 新概念型问题

中考数学专题 新概念型问题

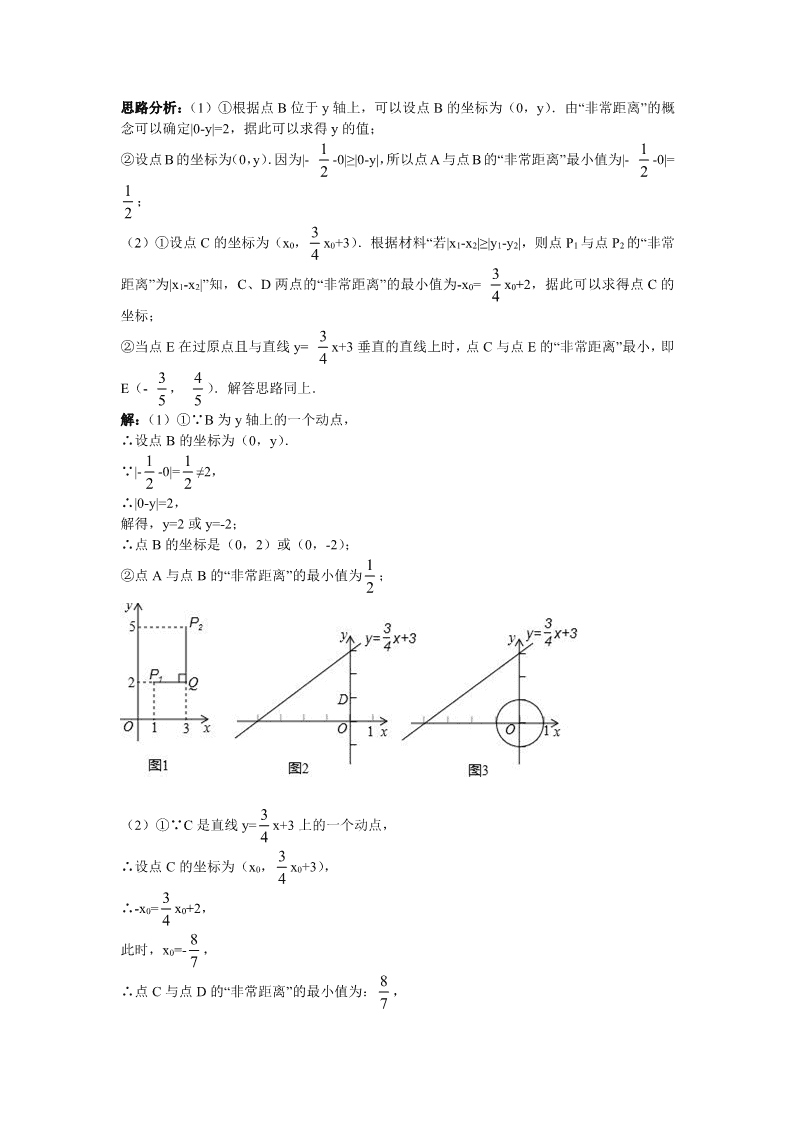
中考数学专题 新概念型问题 一、中考专题诠释 所谓“新概念”型问题，主要是指在问题中概念了中学数学中没有学过的一些概念、新运算、新符号，要求学生读懂题意并结合已有知识、能力进行理解，根据新概念进行运算、推理、迁移的一种题型.“新概念”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视学生应用新的知识解决问题的能力 二、解题策略和解法精讲 ‎“新概念型专题”关键要把握两点：一是掌握问题原型的特点及其问题解决的思想方法；二是根据问题情景的变化，通过认真思考，合理进行思想方法的迁移．‎ 三、中考典例剖析 考点一：规律题型中的新概念 例1我们把按照一定顺序排列的一列数称为数列，如1，3，9，19，33，…就是一个数列，如果一个数列从第二个数起，每一个数与它前一个数的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做这个等差数列的公差．如2，4，6，8，10就是一个等差数列，它的公差为2．如果一个数列的后一个数与前一个数的差组成的新数列是等差数列，则称这个数列为二阶等差数列．例如数列1，3，9，19，33，…，它的后一个数与前一个数的差组成的新数列是2，6，10，14，…，这是一个公差为4的等差数列，所以，数列1，3，9，19，33，…是一个二阶等差数列．那么，请问二阶等差数列1，3，7，13，…的第五个数应是 21‎ ‎．‎ 对应训练 ‎1．若x是不等于1的实数，我们把 称为x的差倒数，如2的差倒数是 =-1，-1的差倒数为 = ，现已知x1=- ，x2是x1的差倒数，x3是x2的差倒数，x4是x3的差倒数，…，依次类推，则x2012= ．‎ 考点二：运算题型中的新概念 例2 将4个数a，b，c，d排成2行、2列，两边各加一条竖直线记成，概念=ad-bc，上述记号就叫做2阶行列式．若=8，则x= 2‎ ‎．‎ 点评：此题考查了整式的混合运算，属于新概念的题型，涉及的知识有：完全平方公式，去括号、合并同类项法则，根据题意将所求的方程化为普通方程是解本题的关键．‎ 对应训练 ‎2．若（x1，y1）•（x2，y2）=x1x2+y1y2，则（4，5）•（6，8）=　 　．‎ 考点三：探索题型中的新概念 例3 如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”． （1）“抛物线三角形”一定是 等腰 三角形； （2）若抛物线y=-x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求b的值； （3）如图，△OAB是抛物线y=-x2+b′x（b′＞0）的“抛物线三角形”，是否存在以原点O为对称中心的矩形ABCD？若存在，求出过O、C、D三点的抛物线的表达式；若不存在，说明理由．‎ ‎ 考点四：开放题型中的新概念 例4 在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“非常距离”，给出如下概念： 若|x1-x2|≥|y1-y2|，则点P1与点P2的“非常距离”为|x1-x2|； 若|x1-x2|＜|y1-y2|，则点P1与点P2的“非常距离”为|y1-y2|． 例如：点P1（1，2），点P2（3，5），因为|1-3|＜|2-5|，所以点P1与点P2的“非常距离”为|2-5|=3，也就是图1中线段P1Q与线段P2Q长度的较大值（点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点）． （1）已知点A（-，0），B为y轴上的一个动点， ①若点A与点B的“非常距离”为2，写出一个满足条件的点B的坐标； ②直接写出点A与点B的“非常距离”的最小值； （2）已知C是直线y=x+3上的一个动点， ①如图2，点D的坐标是（0，1），求点C与点D的“非常距离”的最小值及相应的点C的坐标； ②如图3，E是以原点O为圆心，1为半径的圆上的一个动点，求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标． ‎ 思路分析：（1）①根据点B位于y轴上，可以设点B的坐标为（0，y）．由“非常距离”的概念可以确定|0-y|=2，据此可以求得y的值； ②设点B的坐标为（0，y）．因为|- -0|≥|0-y|，所以点A与点B的“非常距离”最小值为|- -0|= ； （2）①设点C的坐标为（x0，x0+3）．根据材料“若|x1-x2|≥|y1-y2|，则点P1与点P2的“非常距离”为|x1-x2|”知，C、D两点的“非常距离”的最小值为-x0= x0+2，据此可以求得点C的坐标； ②当点E在过原点且与直线y= x+3垂直的直线上时，点C与点E的“非常距离”最小，即E（- ， ）．解答思路同上．‎ 解：（1）①∵B为y轴上的一个动点， ∴设点B的坐标为（0，y）． ∵|--0|=≠2， ∴|0-y|=2， 解得，y=2或y=-2； ∴点B的坐标是（0，2）或（0，-2）； ②点A与点B的“非常距离”的最小值为； （2）①∵C是直线y=x+3上的一个动点， ∴设点C的坐标为（x0，x0+3）， ∴-x0=x0+2， 此时，x0=-， ∴点C与点D的“非常距离”的最小值为：， ‎ 此时C（-，）； ②E（-，）． --x0=x0+3-， 解得，x0=-， 则点C的坐标为（-，）， 最小值为1．‎ 点评：本题考查了一次函数综合题．对于信息给予题，一定要弄清楚题干中的已知条件．本题中的“非常距离”的概念是正确解题的关键．‎ 对应训练 ‎4．（2012•台州）请你规定一种适合任意非零实数a，b的新运算“a⊕b”，使得下列算式成立： 1⊕2=2⊕1=3，（-3）⊕（-4）=（-4）⊕（-3）=- ，（-3）⊕5=5⊕（-3）=- ，… 你规定的新运算a⊕b= （用a，b的一个代数式表示）．‎ 考点五：阅读材料题型中的新概念 将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]． （1）如图①，对△ABC作变换[60°，]得△AB′C′，则S△AB′C′：S△ABC= 3‎ ‎；直线BC与直线B′C′所夹的锐角为 60‎ 度； （2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值； （3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=l，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值． ‎