高考安徽卷理科数学试题及答案

高考安徽卷理科数学试题及答案

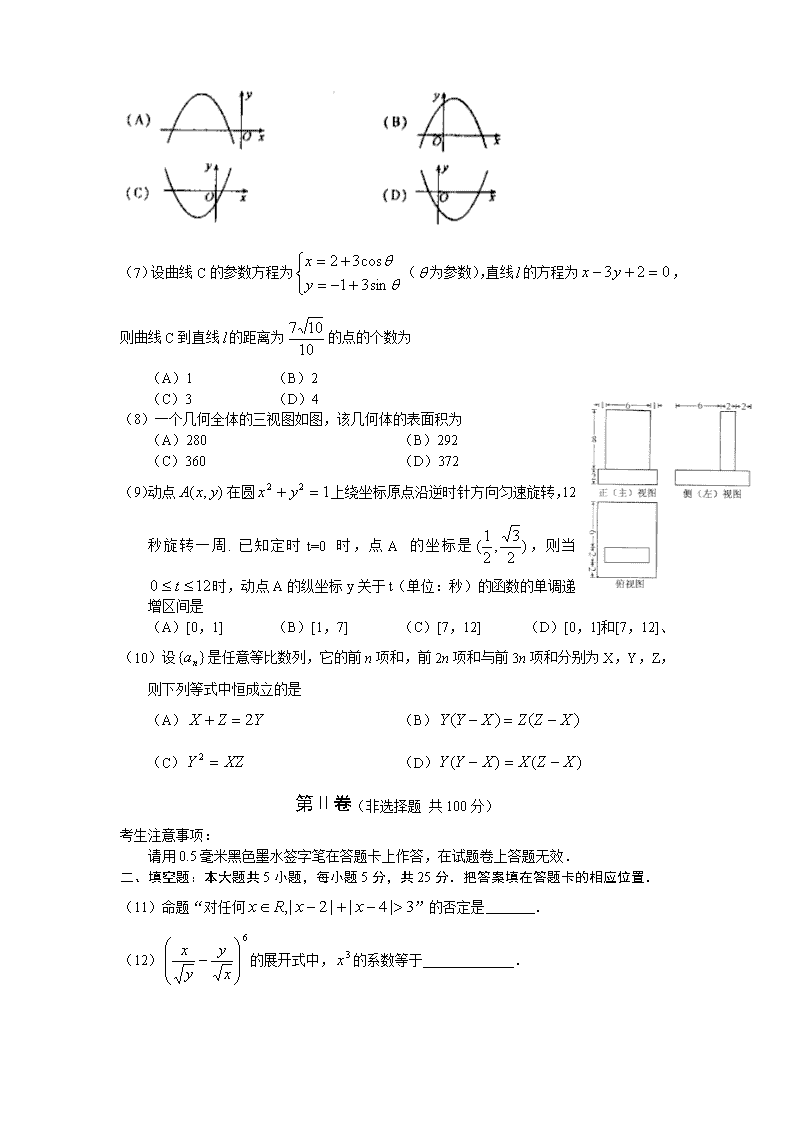
‎2010年高考安徽卷理科数学试题及答案 源头学子 http://www.wxckt.cn 特级教师王新敞 wxckt@126.com 参考公式：‎ 如果事件与互斥，那么 ‎ 如果与是两个任意事件，，那么如果事件与相互独立，那么 ‎ 第Ⅰ卷（选择题，共50分）‎ 一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎（1）是虚数单位，‎ ‎（A） （B） （C） （D）‎ ‎（2）若集合，则 ‎（A） （B）‎ ‎（C） （D）‎ ‎（3）设向量，则下列结论中正确的是 ‎ （A） （B） （C）垂直 （D）‎ ‎（4）若是R上周期为5的奇函数，且满足则=‎ ‎ （A）-1 （B）1 （C）-2 （D）2‎ ‎（5）双曲线方程为，则它的右焦点坐标为 ‎ （A） （B） （C） （D）‎ ‎（6）设，二次函数的图象可能是 ‎（7）设曲线C的参数方程为（为参数），直线的方程为，则曲线C到直线的距离为的点的个数为 ‎ （A）1 （B）2 ‎ ‎ （C）3 （D）4‎ ‎（8）一个几何全体的三视图如图，该几何体的表面积为 ‎ （A）280 （B）292 ‎ ‎ （C）360 （D）372‎ ‎（9）动点在圆上绕坐标原点沿逆时针方向匀速旋转，12秒旋转一周.已知定时t=0时，点A的坐标是，则当时，动点A的纵坐标y关于t（单位：秒）的函数的单调递增区间是 ‎ （A）[0，1] （B）[1，7] （C）[7，12] （D）[0，1]和[7，12]、‎ ‎（10）设是任意等比数列，它的前n项和，前2n项和与前3n项和分别为X，Y，Z，则下列等式中恒成立的是 ‎ （A） （B）‎ ‎ （C） （D）‎ 第Ⅱ卷（非选择题 共100分）‎ 考生注意事项：‎ ‎ 请用0.5毫米黑色墨水签字笔在答题卡上作答，在试题卷上答题无效．‎ 二、填空题：本大题共5小题，每小题5分，共25分．把答案填在答题卡的相应位置．‎ ‎（11）命题“对任何”的否定是 ．‎ ‎（12）的展开式中，的系数等于 ．‎ ‎（13）设满足约束条件若目标函数的最大值为8，则的最小值为 ．‎ ‎（14）如图所示，程序框图（算法流程图）的输出值 ．‎ ‎（15）甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球，先从甲罐中随机取出一球放入乙罐，分别以A1，A2和A3表示由甲罐取出的球是红球，白球和黑球的事件；再从乙罐中随机取出一球，以B表示由乙罐取出的球是红球的事件，则下列结论中正确的是　　（写出所有正确结论的编号）．‎ ‎ ①；‎ ‎ ②；‎ ‎ ③事件B与事件A1相互独立；‎ ‎ ④A1，A2，A3是两两互斥的事件；‎ ‎ ⑤的值不能确定，因为它与A1，A2，A3中究竟哪一个发生有关．‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤，解答写在答题卡上的指定区域内．‎ ‎（16）（本小题满分12分）‎ ‎ 设是锐角三角形，分别是内角A，B，C所对边长，并且 ‎ （Ⅰ）求角A的值；‎ ‎ （Ⅱ）若，求（其中）．‎ ‎（17）（本小题满分12分）‎ 设a为实数，函数 ‎ （I）求的单调区间与极值；‎ ‎ （II）求证：当时，‎ ‎（18）（本小题满分13分）‎ 如图，在多面体ABCDEF中，四边形ABCD是正方形，EF//AB，EF⊥FB，AB=2EF，‎ BF=FC，H为BC的中点.‎ ‎ （I）求证：FH//平面EDB；‎ ‎ （II）求证：AC⊥平面EDB；‎ ‎ （III）求二面角B—DE—C的大小. ‎ ‎（19）（本小题满分13分）‎ 已知椭圆E经过点A（2，3），对称轴为坐标轴，焦点F1，F2在x轴上，离心率 ‎ （I）求椭圆E的方程；‎ ‎ （II）求的角平分线所在直线的方程；‎ ‎ （III）在椭圆E上是否存在关于直线对称的相异两点？若存在，请找出；若不存在，说明理由.‎ ‎（20）（本小题满分12分）‎ 设数列中的每一项都不为0.‎ 证明，为等差数列的充分必要条件是：‎ 对任何，都有 ‎（21）（本小题满分13分）‎ 品酒师需要定期接受酒味鉴别功能测试，一种通常采用的测试方法如下：拿出n瓶外观相同但品质不同的酒让其品尝，要求其按品质优劣为它们排序，经过一段时间，等其记忆淡忘之后，再让其品尝这n瓶酒，并重新按品质优劣为它们排序，这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.‎ 现设n=4，分别以表示第一次排序时被排为1，2，3，4的四种酒在第二次排序时的序号，并令则X是对两次排序的偏离程度的一种描述.‎ ‎ （I）写出X的可能值集合；‎ ‎ （II）假设等可能地为1，2，3，4的各种排列，求X的分布列；‎ ‎ （III）某品酒师在相继进行的三轮测试中，都有，‎ ‎ （i）试按（II）中的结果，计算出现这种现象的概率（假定各轮测试相互独立）；‎ ‎ （ii）你认为该品酒师的酒味鉴别功能如何？说明理由.‎ ‎2010年高考安徽卷理科数学参考答案 一、选择题：本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎（1）B （2）A （3）C （4）A （5）C ‎（6）D （7）B （8）C （9）D （10）D ‎1. B 解析：本题考查了复数的四则运算问题。‎ 由于===+i；‎ ‎2. A 解析：本题考查了对数不等式的求解及集合的运算。‎ 由于A={x|x≥}={x|x≥}={x|0}；‎ ‎3. C 解析：本题考查了平面向量的坐标运算、平面向量的位置关系等。‎ 由于a=（1，0），b=（，），那么|a|=1，|b|=，选项A错；a•b=1×+0×=，选项B错；（a－b）•b=（，－）•（，）=×－×=0，即a－b与b垂直，选项C正确；≠，选项D错.‎ ‎4. A 解析：本题考查了函数的周期性、奇偶性及函数值与运算问题。‎ 由于f（x）是R上周期为5的奇函数，那么f（3）=f（3－5）=f（－2）=－f（2）=－2，f（4）=f（4－5）=f（－1）=－f（1）=－1，则f（3）－f（4）=－2－（－1）=－1；‎ ‎5. C 解析：本题考查了双曲线的几何性质。‎ 由于双曲线方程为x2－2y2=1，即x2－=1，那么a2=1，b2=，则有c2=a2+b2=，即c=，那么对应的右焦点坐标为（，0）；‎ ‎6. D 解析：本题考查了二次函数的图象与参数的关系。‎ 由于abc>0，那么当a>0时，对应的图象开口朝上，有bc>0，对称轴x=－<0时，有b>0，此时c>0，选项C错误；对称轴x=－>0时，有b>0，此时c>0，选项D正确；‎ ‎7. B 解析：本题考查了圆的参数方程，直线与圆的位置关系，点到直线的距离公式等。‎ 由曲线C的参数方程得对应的圆的圆心坐标为C（2，－1），半径r=3，那么C（2，－1）到直线x－3y+2=0的距离d==，那么曲线C与直线l相切，则C上到直线l距离为的点有2个；‎ ‎8. C 解析：本题考查了简单几何体的三视图与直观图的转化，以及简单几何体的表面积计算问题。‎ 由图中的三视图知，该几何体是由两个长方体组成的简单组合体，下面是一个长、宽、高分别为8、10、2的长方体，上面竖着是一个长、宽、高分别为6、2、8的长方体，那么其表面积等于下面长方体的表面积与上面长方体的侧面积之和，即S=2（8×10+8×2+10×2）+2（6×8+2×8）=360；‎ ‎9. D 解析：本题考查了平面解析几何的创新应用，三角函数概念及其三角函数的图象与性质等。‎ 由于12秒旋转一周，则每秒转过=，而t=0时，y==sin，那么动点A的纵坐标关于t的函数关系式为y=sin（t+）（t∈[0，12]），则对应的单调递增区间为t+∈[2kπ－，2kπ+]，k∈Z，则有t∈[12k－5，12k+1]，k∈Z，由于t∈[0，12]，则当k=0时，t∈[0，1]，当k=1时，t∈[7，12]；‎ ‎10. D 解析：本题考查了等比数列前n项的相关性质及其应用。‎ 由于等比数列{an}中Sn=X，S2n=Y，S3n=Z，根据等比数列的相关性质，对应的Sn，S2n－Sn，S3n－S2n也成等比数列，即X，Y－X，Z－Y成等比数列，则有（Y－X）2=X（Z－Y），即Y（Y－X）=X（Z－X）；‎ 二、填空题：本大题共5小题，每小题5分，共25分．把答案填在答题卡的相应位置．‎ ‎（11）存在 ‎（12）15（若只写，也可）‎ ‎（13）4 （14）12 （15）②④‎ ‎11. “存在x∈R，有|x－2|+|x－4|≤‎3”‎ 解析：本题考查了存在命题的否定。‎ 由于存在命题的否定是全称命题，对应“对任何x∈R，|x－2|+|x－4|>‎3”‎的否定就是“存在x∈R，有|x－2|+|x－4|≤‎3”‎；‎ ‎12. 15 解析：本题考查了二项展开式的性质与通项公式等。‎ 由于二项展开式的通项为Tr+1=（）6－r（－）r=（－1）r•••，令6－r=3，解得r=2，那其对应的系数为（－1）2•=15；‎ ‎13. 4 解析：本题考查了线性规划中的平面区域与函数值最值问题，以及利用基本不等式来求解最值问题。‎ 作出平面区域，如图中的阴影部分，由图知，当过点A（1，4）时，z=abx+y取得最大值8，此－ab==－4，即ab=4，而a>0，b>0，那么a+b≥2=4，当且仅当a=b=2时等号成立；‎ ‎14. 12 解析：本题考查了算法中的程序框图的识别与应用。‎ 当x=1时，经过判断其是奇数，则有x=1+1=2；经过判断其是偶数，则有x=2+2=4，经过判断x<8，则有x=4+1=5，经过判断其是奇数，则有x=5+1=6；经过判断其是偶数，则有x=6+2=8，经过判断x=8，则有x=8+1=9，经过判断其是奇数，则有x=9+1=10；经过判断其是偶数，则有x=10+2=12，经过判断x>8，输出x=12；‎ ‎15. ②④ 解析：本题考查了随机事件的概率，条件概率和互斥事件等问题。‎ 根据题意可得P（A1）=，P（A2）=，P（A3）=，可以判断④是正确的；而P（B）=×+×+×=，则①是错误的；由于P（B|A1）===，则②是正确的；同时可以判断出③和⑤是错误的；‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤，解答写在答题卡上的指定区域内．‎ ‎（16）（本小题满分12分）‎ ‎ 本题考查两角和的正弦公式，同角三角函数的基本关系，特殊角的三角函数值，向量的数量积，利用余弦定理解三角形等有关知识，考查综合运算求解能力.‎ ‎ 解：（I）因为 ‎ ‎ ‎ （II）由可得 ‎ ①‎ ‎ 由（I）知所以 ‎ ②‎ 由余弦定理知 及①代入，得 ③‎ ‎③+②×2，得，‎ 所以 ‎ 因此，c，b是一元二次方程的两个根.‎ 解此方程并由 ‎（17）（本小题满分12分）‎ 本题考查导数的运算，利用导数研究函数的单调区间，求函数的极值和证明函数不等式，考查运算能力、综合分析和解决问题的能力.‎ ‎ （I）解：由 令的变化情况如下表：‎ ‎—‎ ‎0‎ ‎+‎ 单调递减 ‎↘‎ 单调递增 ‎↗‎ 故的单调递减区间是，单调递增区间是，‎ 处取得极小值，‎ 极小值为 ‎ （II）证：设 于是 由（I）知当 于是当 而 即 ‎（18）（本小题满分13分）‎ ‎ 本题考查空间线面平行、线面垂直、面面垂直的判断与证明，考查二面角的求法以及利用向量知识解决几何问题的能力，同时考查空间想象能力、推理论证能力和运算能力.‎ ‎ [综合法]（1）证：设AC与BD交于点G，则G为AC的中点，连EG，GH，‎ ‎ 又H为BC的中点，‎ ‎ ∴四边形EFHG为平行四边形，‎ ‎∴EG//FH，而EG平面EDB，∴FH//平面EDB.‎ ‎ （II）证：由四边形ABCD为正方形，有AB⊥BC，又EF//AB，‎ ‎∴EF⊥BC.‎ 而EF⊥FB，∵EF⊥平面BFC，∴EF⊥FH，∴AB⊥FH.‎ 又BF=FC，H为BC的中点，∴FH⊥BC.‎ ‎∴FH⊥平面ABCD，∴FH⊥AC，‎ 又FH//BC，∴AC=EG.‎ 又AC⊥BD，EGBD=G，∴AG⊥平面EDB.‎ ‎ （III）解：EF⊥FB，∠BFC=90°，∴BF⊥平面CDEF， ‎ 在平面CDEF内过点F作FK⊥DE交DE的延长线于K，‎ 则∠FKB为二面角B—DE—C的一个平面角.‎ 设EF=1，则AB=2，FC=，DE=‎ 又EF//DC，∴∠KEF=∠EDC，∴sin∠EDC=sin∠KEF=‎ ‎∴FK=EFsin∠KEF=，tan∠FKB=∴∠FKB=60°‎ ‎∴二面角B—DE—C为60°.‎ ‎[向量法]‎ ‎∵四边形ABCD为正方形，∴AB⊥BC，又EF//AB，∴EF⊥BC.‎ 又EF⊥FB，∴EF⊥平面BFC.‎ ‎∴EF⊥FH，∴AB⊥FH.‎ 又BF=FC，H为BC的中点，∴FH⊥BC，∴FH⊥平面ABC.‎ 以H为坐标原点，轴正向，轴正向， ‎ 建立如图所示坐标系.‎ 设BH=1，则A（1，—2，0），B（1，0，0），‎ C（—1，0，0），D（—1，—2，0），E（0，—1，1），‎ F（0，0，1）.‎ ‎ （I）证：设AC与BD的交点为G，连GE，GH，‎ 则 平面EDB，HF不在平面EDB内，∴FH∥平面EBD，‎ ‎ （II）证： ‎ 又AC⊥BD，EG∩BD=G，∴AC⊥平面EDB.‎ ‎ （III）解：‎ 设平面BDE的法向量为 则 即二面角B—DE—C为60°.‎ ‎（19）（本小题满分13分）‎ ‎ 本题考查椭圆的定义及标准方程，椭圆的简单几何性质，直线的点斜式方程与一般方程，点到直线的距离公式，点关于直线的对称等基础知识；考查解析几何的基本思想、综合运算能力、探究意识与创新意识.‎ 解：（I）设椭圆E的方程为 将A（2，3）代入上式，得 ‎∴椭圆E的方程为 ‎ （II）解法1：由（I）知，所以 直线AF1的方程为：‎ 直线AF2的方程为：‎ 由点A在椭圆E上的位置知，直线l的斜率为正数.‎ 设上任一点，则 若（因其斜率为负，舍去）.‎ 所以直线l的方程为：‎ 解法2：‎ ‎ （III）解法1：假设存在这样的两个不同的点 由于M在l上，故 ①‎ 又B，C在椭圆上，所以有 两式相减，得 即 将该式写为，‎ 并将直线BC的斜率和线段BC的中点，表示代入该表达式中，‎ 得 ②‎ ‎①×2—②得，即BC的中点为点A，而这是不可能的.‎ ‎∴不存在满足题设条件的点B和C.‎ 解法2：‎ 假设存在，‎ 则 得一元二次方程 则是该方程的两个根，‎ 由韦达定理得 于是 ‎∴B，C的中点坐标为 又线段BC的中点在直线 即B，C的中点坐标为（2，3），与点A重合，矛盾.‎ ‎∴不存在满足题设条件的相异两点.‎ ‎（20）（本小题满分12分）‎ 本题考查等差数列、数学归纳法与充要条件等有关知识，考查推理论证、运算求解能力.‎ 证：先证必要性 设数列则所述等式显然成立，‎ 若，则 再证充分性.‎ 证法1：（数学归纳法）设所述的等式对一切都成立，首先，在等式 ‎ ①‎ 两端同乘成等差数列，‎ 记公差为 假设时，观察如下二等式 ‎ ②‎ ‎， ③‎ 将②代入③，得 在该式两端同乘 将 由数学归纳法原理知，对一切 所以的等差数列.‎ 证法2：[直接证法]依题意有 ‎ ①‎ ‎ ②‎ ‎②—①得 ‎，‎ 在上式两端同乘 同理可得 ③‎ ‎③—④得 即是等差数列，‎ ‎（21）（本小题满分13分）‎ 本题考查离散型随机变量及其分布列，考查在复杂场合下进行计数的能力，能过设置密切贴近生产、生活实际的问题情境，考查概率思想在现实生活中的应用，考查抽象概括能力、应用与创新意识.‎ 解：（I）X的可能值集合为{0，2，4，6，8}.‎ 在1，2，3，4中奇数与偶数各有两个，所以中的奇数个数等于 中的偶数个数，因此的奇偶性相同，‎ 从而必为偶数.‎ X的值非负，且易知其值不大于8.‎ 容易举出使得X的值等于0，2，4，6，8各值的排列的例子.‎ ‎ （II）可用列表或树状图列出1，2，3，4的一共24种排列，计算每种排列下的X值，在等可能的假定下，得到 X ‎0 2 4 6 8‎ P ‎ ‎ ‎ （III）（i）首先，将三轮测试都有的概率记做p，由上述结果和独立性假设，得 ‎ ‎ ‎ （ii）由于是一个很小的概率，这表明如果仅凭随机猜测得到三轮测试都有的结果的可能性很小，所以我们认为该品酒师确实有良好的味觉鉴别功能，不是靠随机猜测.‎ ‎2010年普通高等学校招生全国统一考试(安徽卷)‎ 数 学(理科)点评 今年高考数学试卷注重对思维的深刻性、灵活性的测查，突出考查学生数学应用能力、实践能力和创新意识，切实把数学建模、数学探究和数学文化融入到数学试题中。试卷命题的一个重要导向是稳为核心，稳中有变，立足基础、突出主干，能力立意、锐意创新。‎ ‎1、试题特点 ‎1、命题坚持稳中求变。题型结构不变，但在考查学生学习数学的过程与方法方面作了有益的尝试，如（19）的第三问设问“若存在，请找出；若不存在，说明理由”，解答是“不存在”，多少出乎考生的意料之外，即使考生顺利解答此题，也会不太相信，仔细检查会消耗一些时间；‎ ‎2、命题坚持能力立意，命题着重检测知识迁移能力，检测理性思维的深度、广度与进一步学习的潜能。‎ ‎3、试题源于教材，在总体稳定的前提下有所创新，同时兼顾不同版本教材。‎ ‎4、求稳的同时注重创新。今年开始命制“可以控制范围”的开放性试题，尝试考查学生的创新意识。如（21）“你认为该品酒师的酒味鉴别功能如何？说明理由”等。‎ ‎5、注意难度系数。与09年相比，今年数学理科卷选择题、填空题稍易；（20）是一道常规试题，但准确书写不易，特别是充要性的复习不到位；（21）如果采用列举法将24种排列全部列出，需要时间和耐心，稍有不慎，失误在所难免。整体看，今年试卷比2009年难。‎ ‎2、改革趋势：‎ ‎1、提高新情景、新题型的处理能力。‎ ‎2、注意数学建模和应用数学知识解决实际问题能力的提高。‎ ‎3、提高阅读和数学阅读能力。‎ ‎4、注重良好心理品质培养。如学习兴趣和学习信心、正确的自我定位、良好的考试心理、考试技巧和刻苦努力，锲而不舍的精神等。‎ ‎5、坚持常规的行之有效的集训方法。注重因材施教，分层推进；注重效率，减负增效，减少重复和不必要的消耗；在学生活动后讲评等。‎ ‎6、重视数学思想方法 ‎7、重视能力培养。如计算能力（尽管高考提倡多考点想，少考点算，但绝不是不要算，数学不少题目都离不开算，包括推理证明题在内；值得我们注意的是由于计算机、计算器的普及，学生作业量的减少，学生的运算能力一般比过去差，往往在高考解题中出现会而不对的现象，引起失分．学生运算能力的强弱，在高考中是很容易拉开分数差距的）思维能力、推理论证能力（学生在解答计算和证明题时，往往对证明题感到更加困难，尤其是比较复杂的综合性题目，不易找到突破口，教学中应加强对复杂问题的分析能力和推理能力的训练，同时，数学表达能力和证题的格式以及规范都应注意训练）　　　‎ ‎【 曾经改变过千万人的经典语录 】过去的一页，能不翻就不要翻，翻落了灰尘会迷了双眼；有些人说不出哪里好，但就是谁都 替代不了； 那些以前说着永不分离的人，早已经散落在天涯了；收拾起心情，继续走吧，错过花，你将收获雨；错过这一个，你才会遇到下一个。‎ 源头学子 http://www.wxckt.cn 特级教师王新敞 wxckt@126.com