- 2021-04-14 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级数学上册第二十四章圆24-4弧长和扇形面积第1课时弧长和扇形面积公式教案新版 人教版
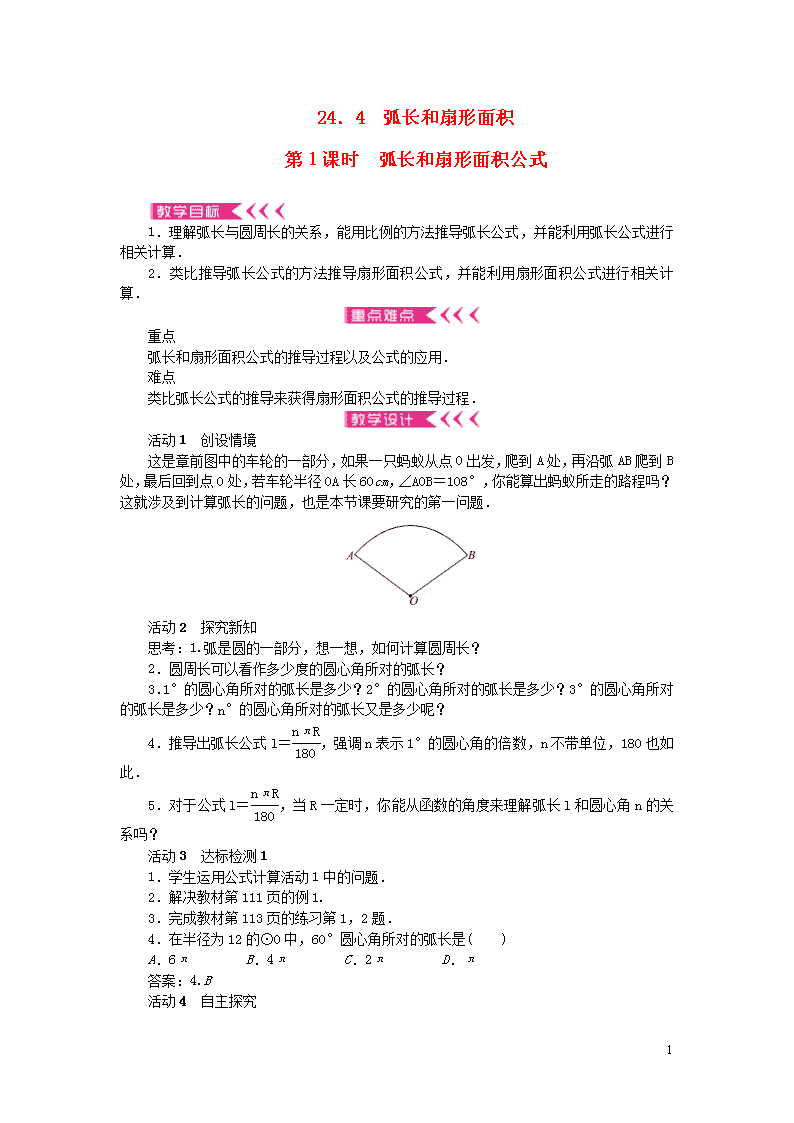
24.4 弧长和扇形面积 第1课时 弧长和扇形面积公式 1.理解弧长与圆周长的关系,能用比例的方法推导弧长公式,并能利用弧长公式进行相关计算. 2.类比推导弧长公式的方法推导扇形面积公式,并能利用扇形面积公式进行相关计算. 重点 弧长和扇形面积公式的推导过程以及公式的应用. 难点 类比弧长公式的推导来获得扇形面积公式的推导过程. 活动1 创设情境 这是章前图中的车轮的一部分,如果一只蚂蚁从点O出发,爬到A处,再沿弧AB爬到B处,最后回到点O处,若车轮半径OA长60 cm,∠AOB=108°,你能算出蚂蚁所走的路程吗?这就涉及到计算弧长的问题,也是本节课要研究的第一问题. 活动2 探究新知 思考:1.弧是圆的一部分,想一想,如何计算圆周长? 2.圆周长可以看作多少度的圆心角所对的弧长? 3.1°的圆心角所对的弧长是多少?2°的圆心角所对的弧长是多少?3°的圆心角所对的弧长是多少?n°的圆心角所对的弧长又是多少呢? 4.推导出弧长公式l=,强调n表示1°的圆心角的倍数,n不带单位,180也如此. 5.对于公式l=,当R一定时,你能从函数的角度来理解弧长l和圆心角n的关系吗? 活动3 达标检测1 1.学生运用公式计算活动1中的问题. 2.解决教材第111页的例1. 3.完成教材第113页的练习第1,2题. 4.在半径为12的⊙O中,60°圆心角所对的弧长是( ) A.6π B.4π C.2π D.π 答案:4.B 活动4 自主探究 3 1.观察问题1中蚂蚁所围成的图形是什么?请学生独立阅读教材第112页第1自然段. 2.我们知道弧是圆的一部分,所以我们把弧长的问题转化为圆周长的问题来解决.那么扇形呢?你能类比弧长的推导方式求出扇形的面积公式吗? 3.比较弧长公式和扇形面积公式,请推导出扇形面积和对应弧长的关系. 活动5 反馈新知 1.已知扇形的半径为3 cm,面积为3π cm2,则扇形的圆心角是________°,扇形的弧长是________cm.(结果保留π)(答案:120,2π) 2.师生共同完成教材第112页例2. 3.完成教材第113页练习第3题. 4.如图,已知扇形的圆心角是直角,半径是2,则图中阴影部分的面积是________.(结果不计算近似值)(答案:π-2) 5.方法小结: 问题1:求一个图形的面积,而这个图形是未知图形时,我 们应该把未知图形化为什么图形呢? 问题2:通过以前的学习,我们又是通过什么方式把未知图形化为已知图形的呢? 活动6 达标检测2 1.120°的圆心角所对的弧长是12π cm,则此弧所在的圆的半径是________. 2.如图,在4×4的方格中(共有16个方格),每个小方格都是边长为1的正方形.O,A,B分别是小正方形的顶点,则扇形OAB的弧长等于________.(结果保留根号及π) 3.如图,矩形ABCD中,AB=1,AD=,以AD的长为半径的⊙A交BC边于点E,则图中阴影部分的面积为________. 答案:1.18 cm;2.π;3.--π. 活动7 课堂小结与作业布置 课堂小结 1.弧长公式是什么?扇形的面积公式呢?是怎样推导出来的?如何理解这两个公式?这两个公式有什么作用?这两个公式有什么联系? 2.在解决部分与整体关系的问题时,我们应学会用什么方法去解决? 3 3.解决不规则图形的面积问题时,我们应用什么数学思想去添加辅助线? 作业布置 教材第115页 习题24.4第1题的(1),(2)题,第2~8题. 3查看更多