高考数学复习 17-18版 第9章 第49课 双曲线
第49课 双曲线
[最新考纲]
内容
要求
A
B
C
中心在坐标原点的双曲线
的标准方程与几何性质
√
1.双曲线的定义
(1)平面内与两个定点F1,F2(F1F2=2c>0)的距离之差的绝对值为非零常数2a(2a<2c)的点的轨迹叫作双曲线.这两个定点叫作双曲线的焦点.
(2)集合P={M|MF1-MF2=2a},F1F2=2c,
其中a,c为常数且a>0,c>0.
①当2a
F1F2时,M点不存在.
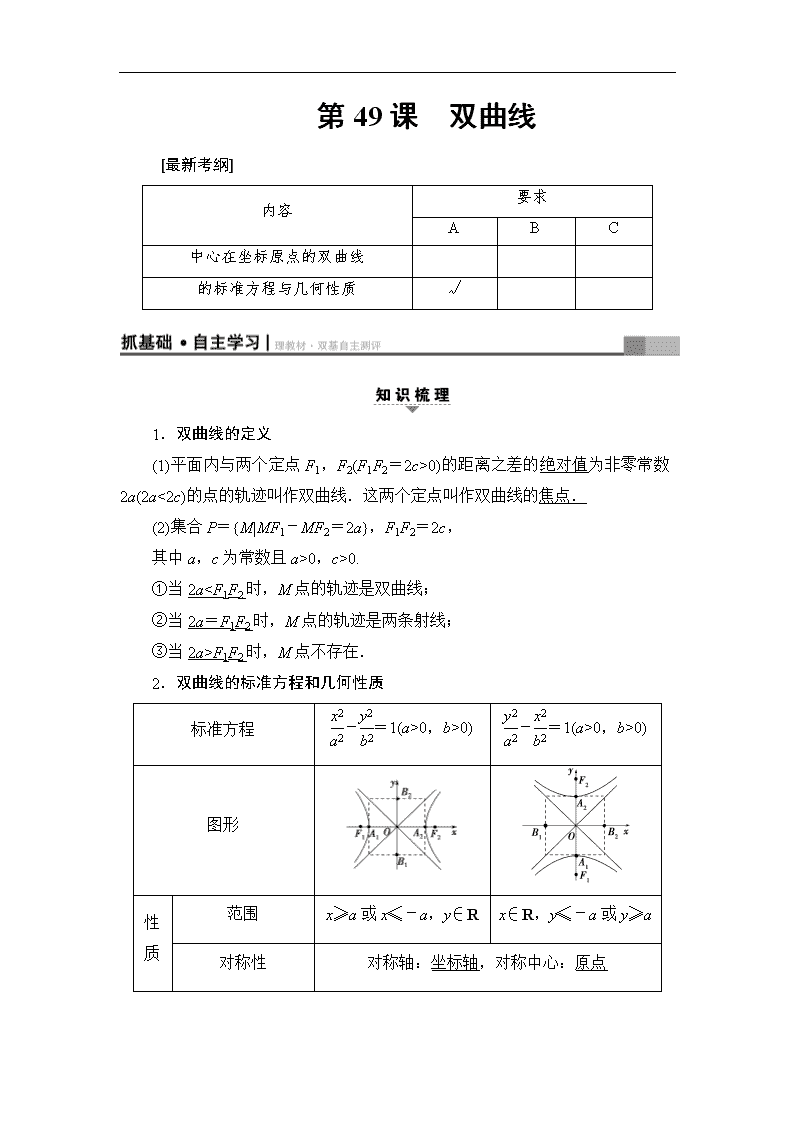
2.双曲线的标准方程和几何性质
标准方程
-=1(a>0,b>0)
-=1(a>0,b>0)
图形
性质
范围
x≥a或x≤-a,y∈R
x∈R,y≤-a或y≥a
对称性
对称轴:坐标轴,对称中心:原点
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
渐近线
y=±x
y=±x
离心率
e=,e∈(1,+∞),其中c=
a,b,c的关系
c2=a2+b2(c>a>0,c>b>0)
3.等轴双曲线
实轴和虚轴等长的双曲线叫作等轴双曲线,其渐近线方程为y=±x,离心率为e=.
1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)平面内到点F1(0,4),F2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.( )
(2)方程-=1(mn>0)表示焦点在x轴上的双曲线.( )
(3)双曲线方程-=λ(m>0,n>0,λ≠0)的渐近线方程是-=0,即±=0.( )
(4)等轴双曲线的渐近线互相垂直,离心率等于.( )
[答案] (1)× (2)× (3)√ (4)√
2.(教材改编)已知双曲线-=1(a>0)的离心率为2,则a=________.
1 [依题意,e===2,
∴=2a,则a2=1,a=1.]
3.(2017·泰州中学高三摸底考试)若双曲线x2-=1的焦点到渐近线的距离为2,则实数k的值是________.
8 [由题意得b=2⇒k=b2=8.]
4.(2016·江苏高考)在平面直角坐标系xOy中,双曲线-=1的焦距是________.
2 [由双曲线的标准方程,知a2=7,b2=3,所以c2=a2+b2=10,所以c=,从而焦距2c=2.]
5.(2016·北京高考改编)已知双曲线-=1(a>0,b>0)的一条渐近线为2x+y=0,一个焦点为(,0),则双曲线的方程为__________.
x2-=1 [由于2x+y=0是-=1的一条渐近线,
∴=2,即b=2a.①
又∵双曲线的一个焦点为(,0),则c=,
由a2+b2=c2,得a2+b2=5,②
联立①②得a2=1,b2=4.
∴所求双曲线的方程为x2-=1.]
双曲线的定义及应用
已知F是双曲线C:x2-=1的右焦点,P是C的左支上一点,A(0,6).则△APF周长的最小值为__________. 【导学号:62172269】
32 [由双曲线方程x2-=1可知,a=1,c=3,
故F(3,0),F1(-3,0),
当点P在双曲线左支上运动时,由双曲线定义知PF-PF1=2.所以PF=PF1+2,
从而△APF的周长=AP+PF+AF=AP+PF1+2+AF.
因为AF==15为定值,
所以当(AP+PF1)最小时,△APF的周长最小,A,F1,P三点共线.
又因为AP+PF1≥AF1=AF=15.
所以△APF周长的最小值为15+15+2=32.]
[规律方法] 1.应用双曲线的定义需注意的问题:
在双曲线的定义中要注意双曲线上的点(动点)具备的几何条件,即“到两定点(焦点)的距离之差的绝对值为一常数,且该常数必须小于两定点间的距离”.若定义中的“绝对值”去掉,点的轨迹是双曲线的一支.同时需注意定义的转化应用.
2.在焦点三角形中,注意定义、余弦定理的活用,常将PF1-PF2=2a平方,建立PF1·PF2间的联系.
[变式训练1] (1)已知双曲线C的离心率为2,焦点为F1,F2,点A在C上.若F1A=2F2A,则cos∠AF2F1=________.
(2)已知双曲线x2-=1的两个焦点为F1,F2,P为双曲线右支上一点.若PF1=PF2,则△F1PF2的面积为________.
(1) (2)24 [(1)由e==2得c=2a,如图,由双曲线的定义得F1A-F2A=2a.
又F1A=2F2A,故F1A=4a,
F2A=2a,
∴cos∠AF2F1==.
(2)由双曲线的定义可得
PF1-PF2=PF2=2a=2,
解得PF2=6,故PF1=8,又F1F2=10,
由勾股定理可知三角形PF1F2为直角三角形,因此S△PF1F2=PF1×PF2=24.]
双曲线的标准方程
(1)已知双曲线C:-=1的离心率e=,且其右焦点为F2(5,0),则双曲线C的方程为________.
(2)(2016·天津高考改编)已知双曲线-=1(a>0,b>0)的焦距为2,且双曲线的一条渐近线与直线2x+y=0垂直,则双曲线的方程为________.
(1)-=1 (2)-y2=1 [(1)由焦点F2(5,0)知c=5.
又e==,得a=4,b2=c2-a2=9.
∴双曲线C的标准方程为-=1.
(2)由焦距为2得c=.因为双曲线的一条渐近线与直线2x+y=0垂直,所以=.
又c2=a2+b2,解得a=2,b=1,
所以双曲线的方程为-y2=1.]
[规律方法] 1.确定双曲线的标准方程也需要一个“定位”条件,两个“定量”条件.“定位”是指确定焦点在哪条坐标轴上,“定量”是指确定a,b的值,常用待定系数法.若双曲线的焦点不能确定时,可设其方程为Ax2+By2
=1(AB<0).
2.对于共焦点、共渐近线的双曲线方程,可灵活设出恰当的形式求解.若已知渐近线方程为mx+ny=0,则双曲线方程可设为m2x2-n2y2=λ(λ≠0).
[变式训练2] (1)已知双曲线过点(4,),且渐近线方程为y=±x,则该双曲线的标准方程为________________.
(2)设椭圆C1的离心率为,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为__________.
(1)-y2=1 (2)-=1 [(1)∵双曲线的渐近线方程为y=±x,
∴可设双曲线的方程为x2-4y2=λ(λ≠0).
∵双曲线过点(4,),
∴λ=16-4×()2=4,
∴双曲线的标准方程为-y2=1.
(2)由题意知椭圆C1的焦点坐标为F1(-5,0),F2(5,0),设曲线C2上的一点P,则PF1-PF2=8.
由双曲线的定义知:a=4,b=3.
故曲线C2的标准方程为-=1,即-=1.]
双曲线的简单几何性质
(1)(2016·全国卷Ⅱ改编)已知F1,F2是双曲线E:-=1的左、右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为________.
(2)设双曲线-=1(a>0,b>0)的右焦点是F,左、右顶点分别是A1,A2,过F作A1A2的垂线与双曲线交于B,C两点.若A1B⊥A2C,则该双曲线的渐近线为__________. 【导学号:62172270】
(1) (2)x±y=0 [(1)如图,因为MF1⊥x轴,所以MF1=.
在Rt△MF1F2中,由sin∠MF2F1=得
tan∠MF2F1=.
所以=,即=,即=,
整理得c2-ac-a2=0,
两边同除以a2得e2-e-1=0.
解得e=(负值舍去).
(2)由题设易知A1(-a,0),A2(a,0),B,C.
因为A1B⊥A2C,
所以·=-1,整理得a=b.
因此该双曲线的渐近线为y=±x,即x±y=0.]
[规律方法] 1.(1)求双曲线的渐近线,要注意双曲线焦点位置的影响;(2)求离心率的关键是确定含a,b,c的齐次方程,但一定注意e>1这一条件.
2.双曲线中c2=a2+b2,可得双曲线渐近线的斜率与离心率的关系=.抓住双曲线中“六点”、“四线”、“两三角形”,研究a,b,c,e间相互关系及转化,简化解题过程.
[变式训练3] (1)(2017·无锡期末)设△ABC是等腰三角形,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为________.
(2)双曲线x2+my2=1的虚轴长是实轴长的2倍,则双曲线的渐近线方程为________.
(1) (2)x±2y=0 [(1)设AB=x,则BC=x,AC=x,
∴2a=x-x,2c=x,
∴e====.
(2)由题意可知a2=1,b2=-m,由于b=2a,故-m=4,∴m=-4.
由x2-4y2=0得x=±2y,即x±2y=0.
∴双曲线的渐近线方程为x±2y=0.]
[思想与方法]
1.求双曲线标准方程的主要方法:
(1)定义法:由条件判定动点的轨迹是双曲线,求出a2,b2,得双曲线方程.
(2)待定系数法:即“先定位,后定量”,如果不能确定焦点的位置,应注意分类讨论或恰当设置简化讨论.
①若已知双曲线过两点,焦点位置不能确定,可设方程为Ax2+By2=1(AB<0).
②当已知双曲线的渐近线方程bx±ay=0,求双曲线方程时,可设双曲线方程为b2x2-a2y2=λ(λ≠0).
③与双曲线-=1有相同的渐近线的双曲线方程可设为-=λ(λ≠0).
2.已知双曲线的标准方程求双曲线的渐近线方程,只需将双曲线的标准方程中“1”改为“0”即可.
[易错与防范]
1.区分双曲线中a,b,c的关系与椭圆中a,b,c的关系,在椭圆中a2=b2+c2,在双曲线中c2=a2+b2.
2.双曲线的离心率大于1,椭圆的离心率e∈(0,1).求它们的离心率,不要忽视这一前提条件,否则会产生增解或扩大取值范围.
3.直线与双曲线有一个公共点时,不一定相切,也可能直线与渐近线平行.
课时分层训练(四十九)
A组 基础达标
(建议用时:30分钟)
1.双曲线x2-=1的两条渐近线方程为________.
y=±2x [由x2-=0得y=±2x,即双曲线的两条渐进线方程为y=±2x.]
2.已知双曲线-y2=1(a>0)的一条渐近线为x+y=0,则a=__________.
【导学号:62172271】
[双曲线-y2=1的渐近线为y=±,已知一条渐近线为x+y=0,即y=-
x,因为a>0,所以=,所以a=.]
3.双曲线-=1的离心率为________.
[∵a2=4,b2=5,
∴c2=9,∴e==.]
4.若双曲线-=1的一条渐近线经过点(3,-4),则此双曲线的离心率为________. 【导学号:62172272】
[由双曲线的渐近线过点(3,-4)知=,∴=.
又b2=c2-a2,∴=,
即e2-1=,∴e2=,∴e=.]
5.已知点F1(-3,0)和F2(3,0),动点P到F1,F2的距离之差为4,则点P的轨迹方程为________.
-=1(x>0) [由题设知点P的轨迹方程是焦点在x轴上的双曲线的右支,设其方程为-=1(x>0,a>0,b>0),由题设知c=3,a=2,b2=9-4=5.
所以点P的轨迹方程为-=1(x>0).]
6.已知F为双曲线C:x2-my2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为________.
[由双曲线方程知a2=3m,b2=3,
∴c==.
不妨设点F为右焦点,则F(,0).
又双曲线的一条渐近线为x-y=0,
∴d==.]
7.(2016·全国卷Ⅰ改编)已知方程-=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是________.
(-1,3) [∵原方程表示双曲线,且两焦点间的距离为4.
∴则
因此-10,即-20,b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为E的两个焦点,且2AB=3BC,则E的离心率是________.
2 [如图,由题意知AB=,BC=2c.
又2AB=3BC,
∴2×=3×2c,即2b2=3ac,
∴2(c2-a2)=3ac,两边同除以a2,并整理得2e2-3e-2=0,解得e=2(负值舍去).]
B组 能力提升
(建议用时:15分钟)
1.已知F为双曲线C:-=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为________.
44 [由双曲线C的方程,知a=3,b=4,c=5,
∴点A(5,0)是双曲线C的右焦点,
且PQ=QA+PA=4b=16,
由双曲线定义,得PF-PA=6,
QF-QA=6.
∴PF+QF=12+PA+QA=28,
因此△PQF的周长为PF+QF+PQ=28+16=44.]
2.已知点F是双曲线-=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
(1,2) [由题意易知点F的坐标为(-c,0),A,B,E(a,0),∵△
ABE是锐角三角形,∴·>0,
即·=·>0,整理得3e2+2e>e4,
∴e(e3-3e-3+1)<0,
∴e(e+1)2(e-2)<0,
解得e∈(0,2),又e>1,∴e∈(1,2).]
3.(2016·北京高考)双曲线-=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点.若正方形OABC的边长为2,则a=__________.
2 [双曲线-=1的渐近线方程为y=±x,易得两条渐近线方程互相垂直,由双曲线的对称性知=1.
又正方形OABC的边长为2,所以c=2,
所以a2+b2=c2=8,因此a=2.]
4.已知双曲线-=1(a>0,b>0)的一个焦点为F(2,0),且双曲线的渐近线与圆(x-2)2+y2=3相切,则双曲线的方程为__________.
x2-=1 [由双曲线的渐近线y=±x,即bx±ay=0与圆(x-2)2+y2=3相切,
∴=,则b2=3a2.①
又双曲线的一个焦点为F(2,0),
∴a2+b2=4,②
联立①②,解得a2=1,b2=3.
故所求双曲线的方程为x2-=1.]
5.(2017·南通三模)在平面直角坐标系xOy中,双曲线-y2=1与抛物线y2=-12x有相同的焦点,则双曲线的两条渐近线的方程为________.
y=±x [抛物线y2=-12x的焦点为(-3,0),∴a2+1=9,∴a=±2.
∴双曲线的两条渐近线方程为y=±=±x.]
6.(2016·天津高考改编)已知双曲线-=1(b>0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A,B,C,D四点,四边形ABCD的面积为2b,则双曲线的方程为________.
-=1 [由题意知双曲线的渐近线方程为y=±x,圆的方程为x2+y2=4,联立
解得或
即第一象限的交点为.
由双曲线和圆的对称性得四边形ABCD为矩形,其相邻两边长为,,故=2b,得b2=12.
故双曲线的方程为-=1.]