- 2021-04-14 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件《三角形的中位线》 (14)_苏科版
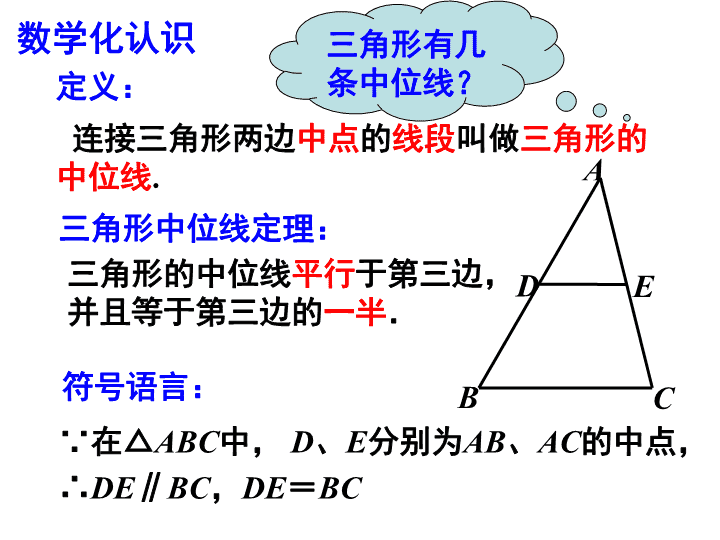
9.5 三角形的中位线 连接三角形两边中点的线段叫做三角形的 中位线. 三角形有几 条中位线? 数学化认识 定义: A B C D E ∵在△ABC中, D、E分别为AB、AC的中点, ∴DE∥BC,DE=BC 三角形中位线定理: 三角形的中位线平行于第三边, 并且等于第三边的一半. 符号语言: A B C D E (a) A B C D E F (b) (1) 如图(a),已知D、E分别为AB和AC 的中点,DE=5,求BC的长; 基础练习 (2) 如图(b),已知D、E、F分别为AB、 AC、BC的中点,AC=8,∠C=70°, 求DF的长和∠EDF的度数; A B C D E F (c) (3) 如图(c),已知D、E、F分别为AB、 AC、BC的中点,若△DEF的周长为10cm, 求△ABC的周长;试想一下如果连接AF, 那么AF与DE有什么关系? 为什么? 基础练习 三角形三条中位线围 成的三角形叫中点三 角形. 例1 如图,在四边形ABCD中,E、F、G、H 分别是四边中点,则四边形EFGH是平行四 边形吗?为什么? 例题讲解 A B F C G D E H 变1:如果改为矩 形ABCD,那四边 形EFGH还是平行 四边形吗?会不会 是特殊的平行四边 形?为什么? 例1 如图,在四边形ABCD中,E、F、G、H 分别是四边中点,则四边形EFGH是平行四 边形吗?为什么? 例题讲解 A B F C G D E H 变2:如果四边形 ABCD不是矩形, 四边形EFGH有没 有可能是菱形?如 果可能,需要添加 什么条件? 例1 如图,在四边形ABCD中,E、F、G、H 分别是四边中点,则四边形EFGH是平行四 边形吗?为什么? 例题讲解 A B F C G D E H 变3:如果改为菱 形ABCD,那四边 形EFGH又会是什 么图形呢?为什么? 例1 如图,在四边形ABCD中,E、F、G、H 分别是四边中点,则四边形EFGH是平行四 边形吗?为什么? 例题讲解 A B F C G D E H 变4:同样的,如 果四边形ABCD不 是菱形,那么四边 形EFGH能成为矩 形吗?如果可能, 需要添加什么条件? 例1 如图,在四边形ABCD中,E、F、G、H 分别是四边中点,则四边形EFGH是平行四 边形吗?为什么? 例题讲解 A B F C G D E H 变5:四边形ABCD 满足什么条件,能 让四边形EFGH成 为正方形? 例2 如图,在四边形ABCD中,AC=BD,E、 F、G、H分别是四边中点. 求证:四边形EFGH是菱形. 例题讲解 A B F C G D E H 归纳总结 (1) 顺次连接四边形中点所得的图形形状跟 哪些因素密切相关? (2) 主要有哪几种情况呢? 1. 顺次连结矩形四边中点所得的四边形是( ) A. 矩形 B. 菱形 C. 正方形 D. 以上都不对 课堂反馈 2. 如果四边形的对角线互相垂直,那么顺次连 结四边形中点所得的四边形是( ) A. 矩形 B. 菱形 C. 正方形 D. 以上都不对 3. 如果顺次连结四边形各边中点组成的四边形 是菱形,那么原来的四边形的对角线( ) A. 互相平分 B. 互相垂直 C. 相等 D. 相等且互相平分 B A C 课堂反馈 4. 顺次连结下列各四边形中点所得的四边形是 矩形的是( ) A. 平行四边形 B. 等腰梯形 C. 矩形 D. 菱形或对角线互相垂直的四边形 D 6. 已知以一个三角形各边中点为顶点的三角 形的周长为8cm,则原三角形的周长为 _____cm 5. 已知三角形的3条中位线分别为3cm、4cm、 6cm,则这个三角形的周长是( ) A. 3cm B. 26cm C. 24cm D. 65cm B 16 7. 如图,A、B两地被建筑物阻隔,为测量A、 B两地的距离,在地面上选一点C,连接CA、 CB,分别取CA、CB的中点D、E. (1) 若DE的长度为36米,求A、B两地之间的 距离. (2) 如果D、E两点之间还有阻隔,你有什么方 法? 课堂反馈 8. 书P87 练习1,2 三角形的中位线有什么性质? 课堂小结 如图,在平行四边形ABCD中,E、F分别 是BC、AD的中点,AE与BF相交于点G, DE与CF相交于点H,试说明GH∥AD且 GH= AD. 2 1 G H E F D A B C 拓展延伸查看更多