- 2021-04-14 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修4教案:2_4_1平面向量数量积的物理背景及其含义
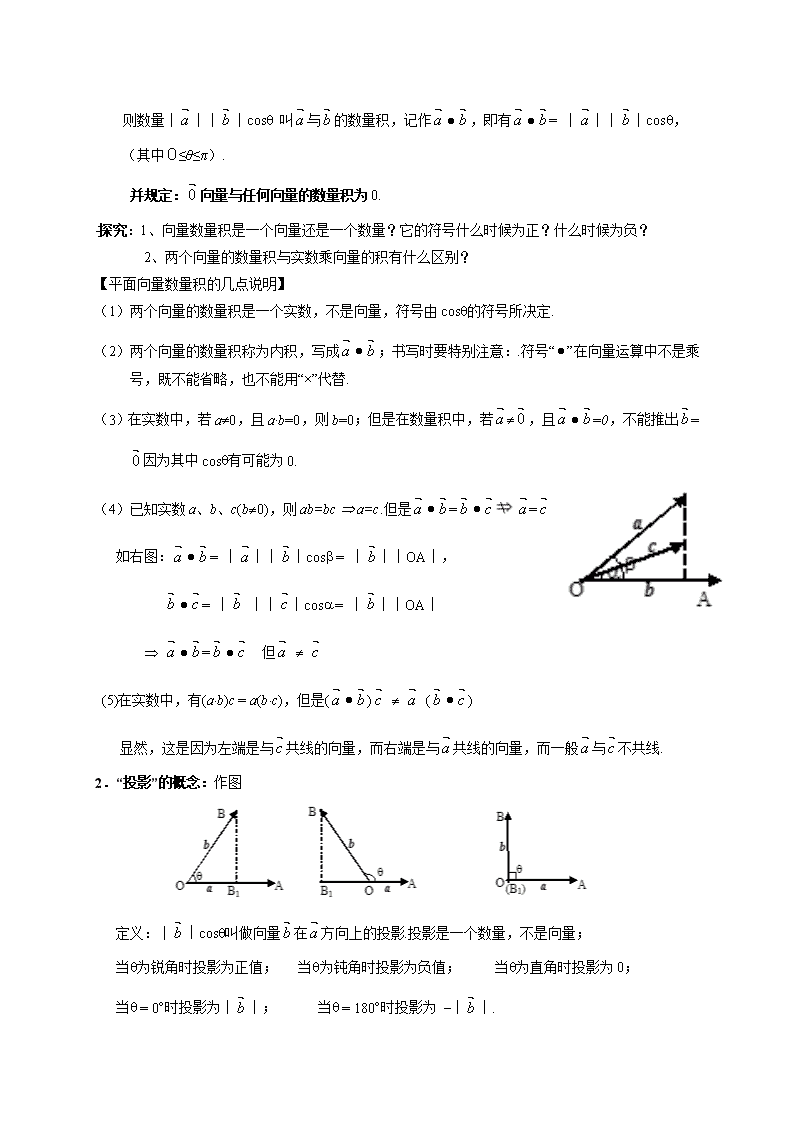
2. 4.1平面向量的数量积的物理背景及其含义 教学目的: 1.掌握平面向量的数量积及其几何意义; 2.掌握平面向量数量积的重要性质及运算律; 3.了解用平面向量的数量积可以处理垂直的问题; 4.掌握向量垂直的条件. 教学重点:平面向量的数量积定义 教学难点:平面向量数量积的定义及运算律的理解和平面向量数量积的应用 教学过程: 一、复习引入: (1)两个非零向量夹角的概念: 已知非零向量与,作=,=,则∠AOB=θ(0≤θ≤π)叫与的夹角. 说明:(1)当θ=0时,与同向; (2)当θ=π时,与反向; (3)当θ=时,与垂直,记⊥; (4)注意在两向量的夹角定义,两向量必须是同起点的.范围是0°≤q≤180° (2)两向量共线的判定定理 (3)练习 1.若=(2,3),=(4,-1+y),且∥,则y=( ) A.6 B.5 C.7 D.8 2.若A(x,-1),B(1,3),C(2,5)三点共线,则x的值为( ) A.-3 B.-1 C.1 D.3 (4)力做的功:W = ||||cosq,q是与的夹角. 功是标量,力和位移是向量,功是由力和位移确定的,类比这种运算,我们引入“数量积”的概念。 二、讲解新课: 1.平面向量数量积(内积)的定义:已知两个非零向量与,它们的夹角是θ, 则数量││││cosq 叫与的数量积,记作,即有= ││││cosq, (其中0≤θ≤π). 并规定:向量与任何向量的数量积为0. ×探究:1、向量数量积是一个向量还是一个数量?它的符号什么时候为正?什么时候为负? 2、两个向量的数量积与实数乘向量的积有什么区别? 【平面向量数量积的几点说明】 (1)两个向量的数量积是一个实数,不是向量,符号由cosq的符号所决定. (2)两个向量的数量积称为内积,写成;书写时要特别注意:.符号“”在向量运算中不是乘号,既不能省略,也不能用“×”代替. (3)在实数中,若a¹0,且a×b=0,则b=0;但是在数量积中,若¹,且=0,不能推出=因为其中cosq有可能为0. (4)已知实数a、b、c(b¹0),则ab=bc Þ a=c.但是== 如右图:= ││││cosb = │││OA│, = │ │││cosa = │││OA│ Þ = 但 ¹ (5)在实数中,有(a×b)c = a(b×c),但是() ¹ () 显然,这是因为左端是与共线的向量,而右端是与共线的向量,而一般与不共线. 2.“投影”的概念:作图 定义:││cosq叫做向量在方向上的投影.投影是一个数量,不是向量; 当q为锐角时投影为正值; 当q为钝角时投影为负值; 当q为直角时投影为0; 当q = 0°时投影为││; 当q = 180°时投影为 -││. 3.向量的数量积的几何意义: 数量积等于的长度与在方向上投影││cosq的乘积. 探究1、:两个向量的数量积的性质:设、为两个非零向量, 1、^ Û = 0 2、当与同向时, = ||||; 当与反向时, = -||||. 特别的×= ||2或 │ │ ≤|||| cosq = 探究2、:平面向量数量积的运算律 (1).交换律: = (2).数乘结合律:()× =(×) = ×() (3).分配律:(+)×=×+× 说明:(1)一般地,(·)≠(·) (2)·=·,≠= (3)有如下常用性质:2=||2, (+)(+)=·+·+·+· 三、讲解范例: 例1.证明:①(+)2=2+2·+2 ②(+)(-)=2-2 例2.已知││=12,││=9,,求与的夹角θ。 例3.已知││=6,││=4,与的夹角为60o求:(1)(+2)·(-3). (2)│+│与│-│. ( 利用 ) 例4.已知││=3,││=4, 且与不共线,k为何值时,向量+k与-k互相垂直. 四、课堂练习: 1.课后练习1、2、3、题 2.已知││=8,││=10,│+│=16,与的夹角θ的余弦. 五、课堂小结: 1.平面向量的数量积及其几何意义; 2.平面向量数量积的重要性质及运算律; 3.向量垂直的条件. 六、作业布置:习题2.4 A组1、2、3、题查看更多