华师版数学八年级下册同步课件-第20章 数据的整理与初步处理-20平均数

华师版数学八年级下册同步课件-第20章 数据的整理与初步处理-20平均数

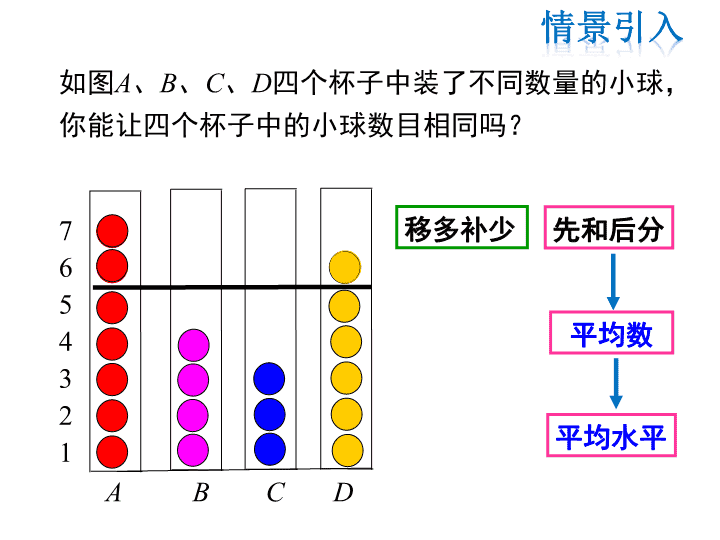
第20章 数据的整理与初步处理 20.1 平均数 1 平均数的意义 2 用计算器求平均数 7 6 5 4 3 2 1 A B C D 平均数 先和后分移多补少 如图A、B、C、D四个杯子中装了不同数量的小球， 你能让四个杯子中的小球数目相同吗？ 平均水平 当你听到“小亮的身高在班上是中等偏上的”， “A 篮球队队员比B 队更年轻”等诸如此类的说 法时，你思考过这些话的含义吗？你知道人们是 如何作出这些判断的吗？ 数学上，我们常借助平均数、中位数、众数、 方差等来对数据进行分析和刻画. 1 平均数 问题1 2018年重庆7月中旬一周的每天最高气温如下： 星期 一 二 三 四 五 六 日 气温/ °C 38 36 38 36 38 36 37 你能快速计算这一周的平均最高气温吗？ 38 36 38 36 38 36 37 =377      问题2 想一想 北京金隅（冠军） 广东东莞银行（亚军） 号码 身高/厘米 年龄/岁 号码 身高/厘米 年龄/岁 3 188 35 3 205 31 6 175 28 5 206 21 7 190 27 6 188 23 8 188 22 7 196 29 9 196 22 8 201 29 10 206 22 9 211 25 12 195 29 10 190 23 13 209 22 11 206 23 20 204 19 12 212 23 21 185 23 20 203 21 25 204 23 22 216 22 31 195 28 30 180 19 32 211 26 32 207 21 51 202 26 0 183 27 哪支球队队 员的身高更 高？哪支球 队的队员更 为年轻？你 是怎样判断 的？与同伴 交流. 思考 日常生活中，我们常用平均数表示一组数 据的“平均水平”. 一般地，如果有 n 个数据 x1，x2，…，xn， 我们把 表示这组数据的平均数， 用“ ” 表示 ，即 1 2 ... n n x x x   x 1 2 ... n n x x xx    ★平均数的概念 植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系. 12 10 8 6 4 2 0 0 请根据图中信息计算： (1)总共有多少人参加了本次活 动？ (2)总共植树多少棵？ (3)平均每人植树多少棵？ 例1 解：（1）参加本次活动的总人数是 1+8+1+10+8+3+1=32（人）. （2）总共植树 3×8+4×1+5×10+6×8+7×3+8×1=155（棵）. （3）平均每人植树 （棵）.155 4.832  12 10 8 6 4 2 0 0 某班级为了解同学年龄情况，作了一次年龄调查， 结果如下：13岁8人，14岁16人，15岁24人，16岁2 人．求这个班级学生的平均年龄（结果取整数）． 13 8 14 16 15 24 16 2 148 16 24 2x + + += + + +      解：这个班级学生的平均年龄为：　 所以，这个班级学生的平均年龄约为14岁．　　　 练一练 丁丁所在的八年级（1）班共有学生40人.下图是 该校各班学生人数分布情况： （1）请计算该校八年级每班平均人数； （2）请计算各班学生人数，并绘制条形统计图. 利用扇形的大小来表示部分占总体的 百分比大小的统计图叫做扇形统计图. 例2 解: 八年级总人数是: 40÷20%=200(人) 八年级每班平均人数是: 200÷5=40(人) 班级人数是: 2班: 200×23%=46(人) 3班: 200×20%=40(人) 4班: 200×18%=36(人) 5班: 200×19%=38(人) 根据表格数据制作各班人数的条形统计图.水平线 上超出部分与下方不足部分在数量上有什么关系？ 班级 1班 2班 3班 4班 5班 人数 40 46 40 36 38 思考 1. 按 ，打开计算器; 2. 按 ，启动计算机功能; 3. 按 输入所有数据: 4.按 ,即可获得这组数据的统计值，其中 平均数为40. ， 你可以根据计算器使用说明书动手试一试，了解怎样修改 已经输入的数据，怎样简便地输入多个相同的数据. 班级 1班 2班 3班 4班 5班 人数 40 46 40 36 38 用计算器求八年级各班学生的平均数 2 用计算器求平均数 1.某商场用单价5元每千克的糖果1千克, 单价7元每千 克的糖果2千克,单价8元每千克的糖果5千克, 混合为 什锦糖果销售, 那么这种什锦糖果的单价是______. (保留1位小数) 7.4元 2. 某次数学测验成绩统计如下: 得100分3人, 得95分 5人,得90分6人, 得80分12人,得70分16人, 得60分5 人, 则该班这次测验的平均得分是______.78.6分 3.已知:x1,x2,x3,…, x10的平均数是a，x11,x12,x13,… ,x30 的平均数是b，则x1,x2,x3,… ,x30的平均数是（ ） A.(a+b) B.(a+b) C.(a+3b)÷3 D.(a+2b)÷3 D 4.若x1,x2,…, xn的平均数为a. (1)则数据x1+3,x2+3,…,xn+3的平均数为 . (2)则数据10x1,10x2,… ,10xn 的平均数为 . a+3 10a 解: 甲的平均成绩为 ， 85 78 85 73 80 254 + + + = . 5.如果公司想招一名综合能力较强的翻译，请计算 两名应聘者的平均成绩，应该录用谁？ 应试者 听 说 读 写 甲 85 78 85 73 乙 73 80 82 83 显然甲的成绩比乙高， 所以从成绩看，应该 录取甲． 平均数 概念 计算公式 用计算器求平均值 1 2 3 nx x x xx n    