2015年高考试题——数学理（湖南卷）原卷版

2015年高考试题——数学理（湖南卷）原卷版

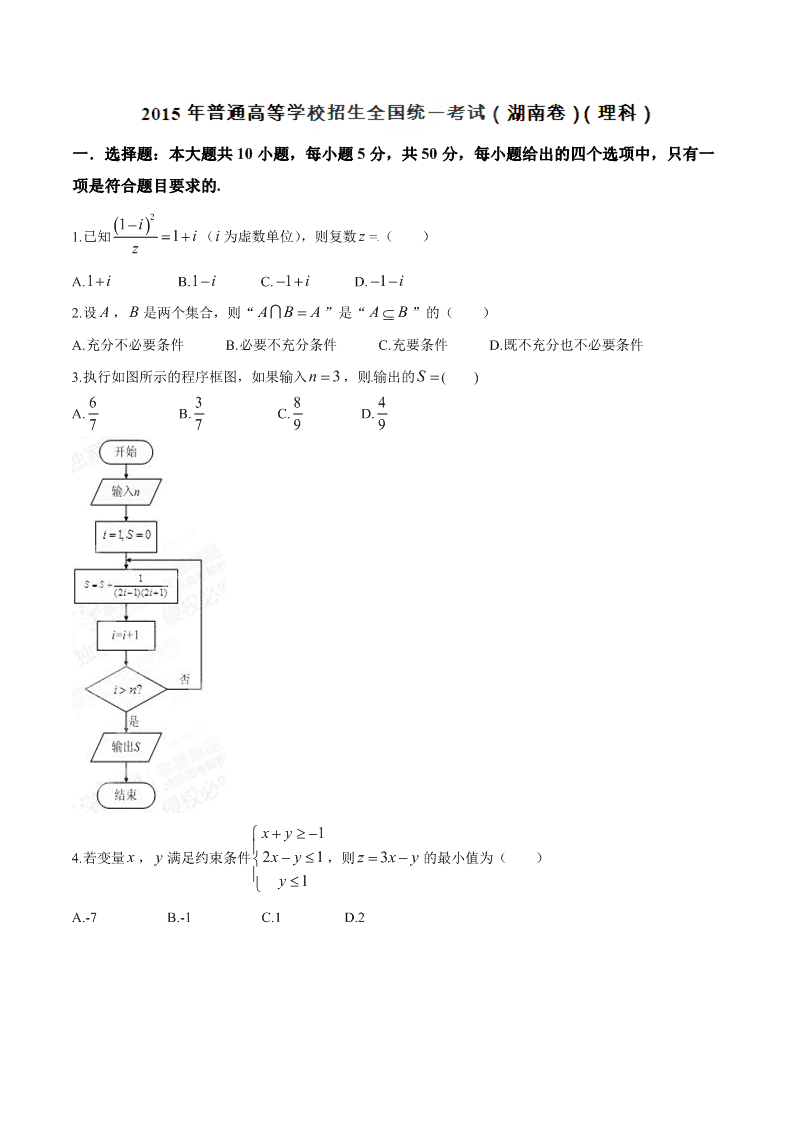
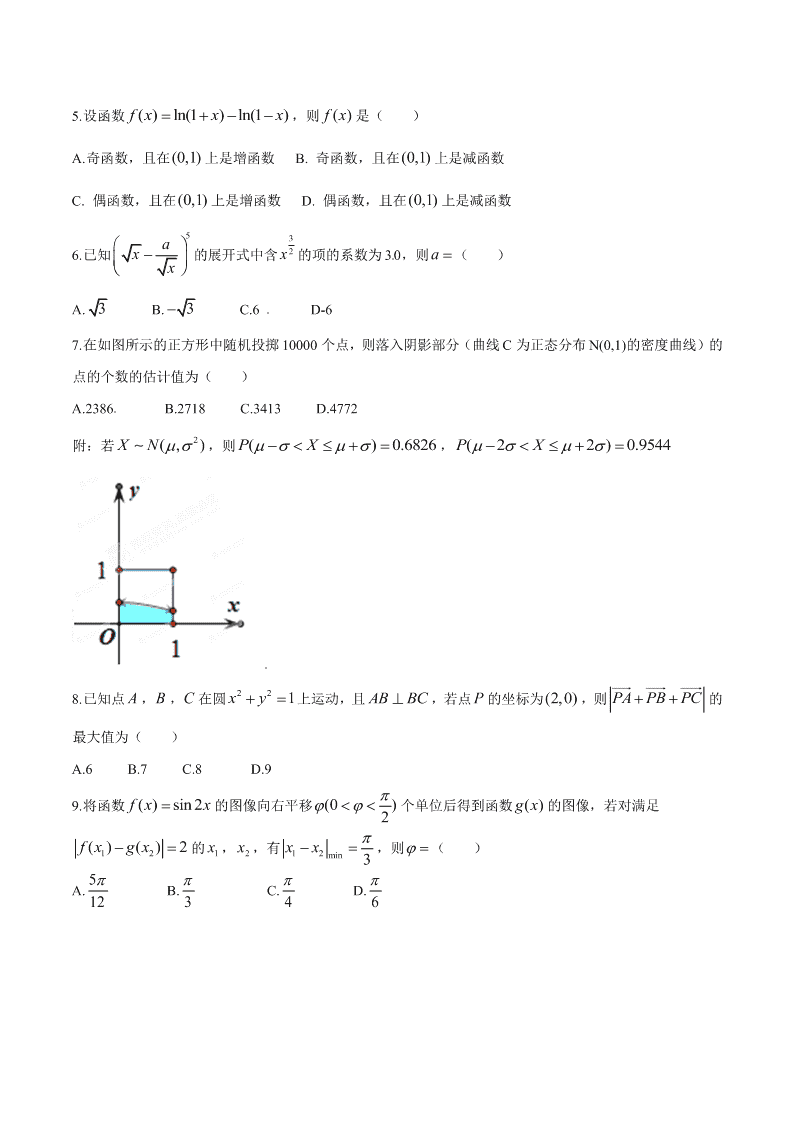
一．选择题：本大题共 10 小题，每小题 5 分，共 50 分，每小题给出的四个选项中，只有一 项是符合题目要求的. 1.已知  21 1i iz  （i 为虚数单位），则复数 z =（ ） A.1 i B.1 i C. 1 i D. 1 i 2.设 A ， B 是两个集合，则“ A B A ”是“ AB ”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3.执行如图所示的程序框图，如果输入 3n  ，则输出的 S  ( ) A. 6 7 B. 3 7 C. 8 9 D. 4 9 4.若变量 x ， y 满足约束条件 1 21 1 xy xy y        ，则 3z x y的最小值为（ ） A.-7 B.-1 C.1 D.2 5.设函数 ( ) ln(1 ) ln(1 )f x x x    ，则 ()fx是（ ） A.奇函数，且在(0,1) 上是增函数 B. 奇函数，且在 上是减函数 C. 偶函数，且在 上是增函数 D. 偶函数，且在 上是减函数 6.已知 5ax x  的展开式中含 3 2x 的项的系数为 30，则 a  （ ） A. 3 B. 3 C.6 D-6 7.在如图所示的正方形中随机投掷 10000 个点，则落入阴影部分（曲线 C 为正态分布 N(0,1)的密度曲线）的 点的个数的估计值为（ ） A.2386 B.2718 C.3413 D.4772 附：若 2( , )XN ，则 6826.0)(   XP ， 9544.0)22(   XP 8.已知点 A ，B ，C 在圆 221xy上运动，且 AB BC ，若点 P 的坐标为(2,0) ，则 PA PB PC 的 最大值为（ ） A.6 B.7 C.8 D.9 9.将函数 ( ) sin 2f x x 的图像向右平移 (0 )2  个单位后得到函数 ()gx的图像，若对满足 12( ) ( ) 2f x g x的 1x ， 2x ，有 12min 3xx ，则  （ ） A. 5 12  B. 3  C. 4  D. 6  10.某工件的三视图如图 3 所示，现将该工件通过切割，加工成一个体积尽可能大的长方体新工件，并使新 工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率= 新工件的体积 原工件的体积 ）（ ） A. 8 9 B. 16 9 C. 34( 2 1)   D. 312( 2 1)   二．填空题：本大题共 5 小题，每小题 5 分，共 25 分.[来源:学,科,网] 11. 2 0 ( 1)x dx   . 12.在一次马拉松比赛中，35 名运动员的成绩（单位：分钟）的茎叶图如图所示，若将运动员按成绩由好到 差编为1 35 号，再用系统抽样方法从中抽取 7 人，则其中成绩在区间[139,151]上的运动员人数是 . 13.设 F 是双曲线C ： 22 221xy ab的一个焦点，若C 上存在点 P ，使线段 PF 的中点恰为其虚轴的一[来源:Zxxk.Com] 个端点，则C 的离心率为 . 14.设 nS 为等比数列 na 的前 n 项和，若 1 1a  ，且 13S ， 22S ， 3S 成等差数列，则 na  . 15.已知 3 2 ,() , x x afx x x a     ，若存在实数b ，使函数 ( ) ( )g x f x b有两个零点，则 a 的取值范围 是 .[来源:学科网] 三．解答题：本大题共 6 小题，共 75 分，解答应写出文字说明、证明过程或演算步骤． 16.（1）如图，在圆O 中，相交于点 E 的两弦 AB ，CD 的中点分别是 M ， N ，直线 MO 与直线CD 相交 于点 F ，证明： （1） 180MEN NOM    ； （2） FE FN FM FO   （Ⅱ）已知直线 35 2: 13 2 xt l yt     （t 为参数），以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系，曲 线C 的极坐标方程为 2cos . （1） 将曲线 C 的极坐标方程化为直角坐标方程； （2） 设点 M 的直角坐标为(5, 3) ，直线l 与曲线 C 的交点为 A ， B ，求| | | |MA MB 的值.[来源:学科网] （Ⅲ）设 0, 0ab，且 11ab ab   . （1） 2ab； （2） 2 2aa与 2 2bb不可能同时成立. 17.设 ABC 的内角 A ， B ，C 的对边分别为 a ，b ，c ， tana b A ，且 B 为钝角. （1）证明： 2BA ； （2）求sin sinAC 的取值范围. 18.某商场举行有奖促销活动，顾客购买一定金额商品后即可抽奖，每次抽奖都从装有 4 个红球、6 个白球 的甲箱和装有 5 个红球、5 个白球的乙箱中，各随机摸出 1 个球，在摸出的 2 个球中，若都是红球，则获一 等奖；若只有 1 个红球，则获二等奖；若没有红球，则不获奖. （1）求顾客抽奖 1 次能获奖的概率； （2）若某顾客有 3 次抽奖机会，记该顾客在 3 次抽奖中获一等奖的次数为 X ，求 X 的分布列和数学期望. .19.如图，已知四棱台 1 1 1 1ABCD A B C D 上、下底面分别是边长为 3 和 6 的正方形， 1 6AA  ，且 1AA  底面 ABCD ，点 P ，Q 分别在棱 1DD ，BC 上. （1）若 P 是 1DD 的中点，证明： 1AB PQ ； （2）若 //PQ 平面 11ABB A ，二面角 P QD A的余弦值为 3 7 ，求四面体 ADPQ 的体积. 20.已知抛物线 2 1 :4C x y 的焦点 F 也是椭圆 22 2 22: 1( 0)yxC a bab    的一个焦点， 1C 与 2C 的公共弦 的长为 26. （1）求 2C 的方程； （2）过点 F 的直线l 与 1C 相交于 A ， B 两点，与 相交于C ， D 两点，且 AC 与 BD 同向 （ⅰ）若| | | |AC BD ，求直线l 的斜率 （ⅱ）设 在点 A 处的切线与 x 轴的交点为 M ，证明：直线 绕点 F 旋转时， MFD 总是钝角三角形 [来源:学#科#网] 21.已知 0a  ，函数 ( ) sin ( [0, ))axf x e x x   ，记 nx 为 ()fx的从小到大的第 n *()nN 个极值点，证 明： （1）数列{ ( )}nfx 是等比数列 （2）若 2 1 1 a e   ，则对一切 *nN ， | ( ) |nnx f x 恒成立.