八年级上数学课件八年级上册数学课件《平均数》 北师大版 (7)_北师大版

八年级上数学课件八年级上册数学课件《平均数》 北师大版 (7)_北师大版

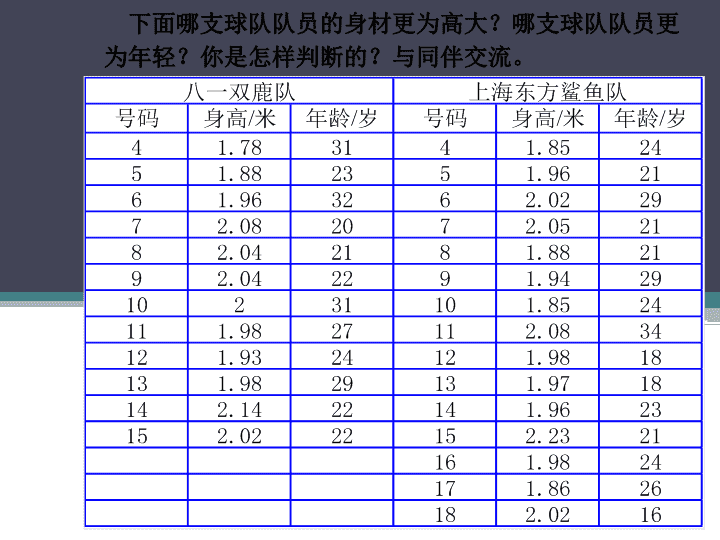
平均数 下面哪支球队队员的身材更为高大？哪支球队队员更 为年轻？你是怎样判断的？与同伴交流。 号码 身高/米 年龄/岁 号码 身高/米 年龄/岁 4 1.78 31 4 1.85 24 5 1.88 23 5 1.96 21 6 1.96 32 6 2.02 29 7 2.08 20 7 2.05 21 8 2.04 21 8 1.88 21 9 2.04 22 9 1.94 29 10 2 31 10 1.85 24 11 1.98 27 11 2.08 34 12 1.93 24 12 1.98 18 13 1.98 29 13 1.97 18 14 2.14 22 14 1.96 23 15 2.02 22 15 2.23 21 16 1.98 24 17 1.86 26 18 2.02 16 八一双鹿队 上海东方鲨鱼队 日常生活中，我们常用平均数 表示一组 数据的“平均水平”。 一般地，对于 n 个数 x1，x2，…，xn， 我们把 ( x1+x2+…+xn ) ÷ n 叫做这 n 个数的 算术平均数，简称平均数。记为 x 。 东方大鲨鱼队队员的平均年龄： 上海东方大鲨鱼队 号码 身高/ 米 年龄/ 岁 4 1.85 24 5 1.96 21 6 2.02 29 7 2.05 21 8 1.88 21 9 1.94 29 10 1.85 24 11 2.08 34 12 1.98 18 13 1.97 18 14 1.96 23 15 2.23 21 16 1.98 24 17 1.86 26 18 2.02 16 平均年龄 = （16×1+18×2+21×4+23×1+24×3+26×1 +29×2+34×1）÷（1+2+4+1+3+1+2+1） ≈23.3（岁） 例： 某广告公司欲招聘广告策划人员一名，对A ， B，C 三名候选人进行了三项素质测试，他们的各 项测试成绩如下表所示： 测试项目 测试成绩 A B C 创 新 72 85 67 综合知识 50 74 70 语 言 88 45 67 （1） 如果根据三项测试的平均成绩决定录用人选， 那么谁将被录用？ （2）根据实际需要，公司将创新、综合知识和语 言三项测试得分按 4∶ 3∶ 1 的比例确定各人的测试 成绩，此时谁将被录用？ 在实际问题中，一组数据里的各个数 据的“重要程度” 未必相同。因而，在 计算这组数据的平均数时，往往给每个 数据一个“权 ”。 　 如例题中 4，3，1 分别是创新、综 合知识、语言三项测试成绩的权，而称 （72×4+50×3+88×1）÷（4+3+1） 为A的三项测试成绩的 加权平均数。 算术平均数是加权平均数各项的 权都相等 的一种特殊情况，即算术 平均数是加权平均数,而加权平均数 不一定是算术平均数。 由于权的不同，导致结果不同，故 权的差异对结果有影响。