- 2021-04-14 发布 |
- 37.5 KB |
- 3页


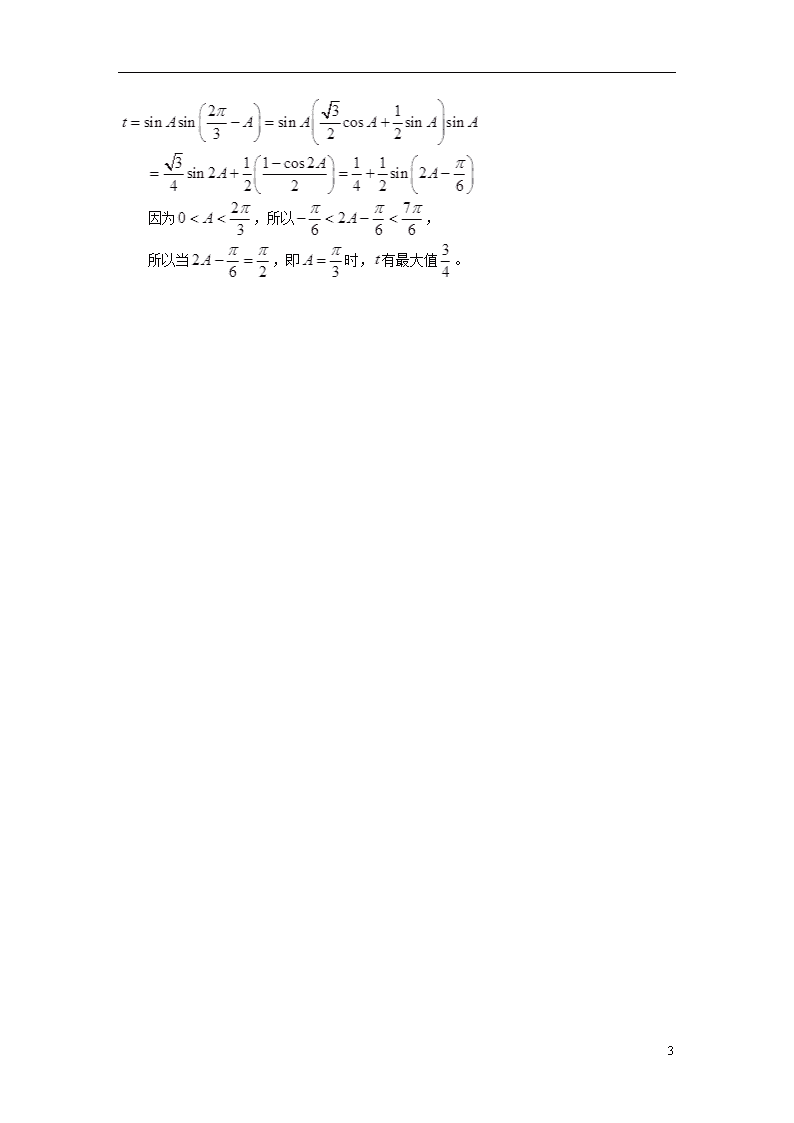
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高中数学 第1章 解三角形余弦定理
余弦定理 (答题时间:40分钟) 1. △ABC的内角的对边分别为,若成等比数列,且,则___________。 2. 在中,,则该三角形最大角的余弦值为__________。 3. 在△ABC中,设AD为BC边上的高,且AD=BC,b,c分别表示角B,C所对的边长,则的取值范围是____________。 4. 设△ABC的内角A,B,C所对的边分别为a,b,c。若(a+b-c)(a+b+c)=ab,则角C=________。 5. 在△ABC中,BC=,AC=1,以AB为边作等腰直角三角形ABD(B为直角顶点,C、D两点在直线AB的两侧)。当变化时,线段CD长的最大值为_________。 *6. 在△ABC中,角A,B,C所对的边分别为a,b,c,已知b=3,c=8,角A为锐角,△ABC的面积为6。 (1)求角A的大小; (2)求a的值。 **7. 在中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列。 (1)若,,求边c的值; (2)设,求t的最大值。 3 1. 解:∵成等比数列,∴,又∵,∴, ∴。 2. 解:先由c2=a2+b2-2abcosC求出c=3,∴最大边为b,最大角为B, ∴cosB=。 3. 解:因为BC边上的高AD=BC=a,所以,则,又, 所以, 其中有tanA=2,又由基本不等式有所以的取值范围。 4. 解:所以 。 5. 解:设,,则在三角形BCD中,由余弦定理可知,在三角形ABC中,由余弦定理可知,可得,所以,令,则,当时等号成立,即CD长的最大值为3。 6. 解:(1)∵S△ABC=bcsinA=×3×8×sinA=6,∴sinA=, ∵A为锐角,∴A=。 (2)由余弦定理知a===7。 7. 解:(1)因为角成等差数列,所以, 因为,所以。 因为,,, 所以, 所以或(舍去)。 (2)因为,所以 3 因为,所以, 所以当,即时,有最大值。 3查看更多