2019年高考数学精讲二轮练习2-5-2

2019年高考数学精讲二轮练习2-5-2

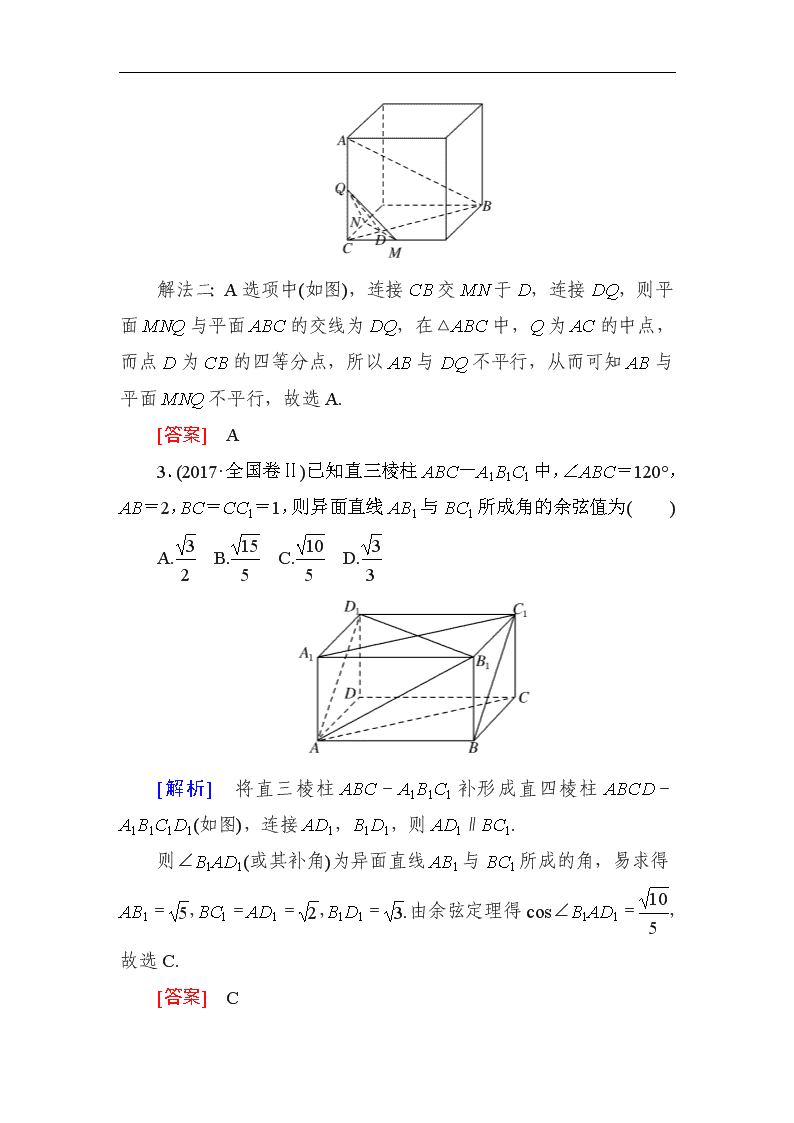
‎1．(2018·浙江卷)已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎[解析]　∵m⊄α，n⊂α，m∥n，∴m∥α，故充分性成立．而由m∥α，n⊂α，得m∥n或m与n异面，故必要性不成立，故选A.‎ ‎[答案]　A ‎2．(2017·全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是(　　)‎ ‎[解析]　解法一：B选项中，AB∥MQ，且AB⊄平面MNQ，MQ⊂平面MNQ，则AB∥平面MNQ；C选项中，AB∥MQ，且AB⊄平面MNQ，MQ⊂平面MNQ，则AB∥平面MNQ；D选项中，AB∥NQ，且AB⊄平面MNQ，NQ⊂平面MNQ，则AB∥平面MNQ，故选A.‎ 解法二：A选项中(如图)，连接CB交MN于D，连接DQ，则平面MNQ与平面ABC的交线为DQ，在△ABC中，Q为AC的中点，而点D为CB的四等分点，所以AB与DQ不平行，从而可知AB与平面MNQ不平行，故选A.‎ ‎[答案]　A ‎3．(2017·全国卷Ⅱ)已知直三棱柱ABC－A1B1C1中，∠ABC＝120°，AB＝2，BC＝CC1＝1，则异面直线AB1与BC1所成角的余弦值为(　　)‎ A. B. C. D. ‎[解析]　将直三棱柱ABC－A1B1C1补形成直四棱柱ABCD－A1B1C1D1(如图)，连接AD1，B1D1，则AD1∥BC1.‎ 则∠B1AD1(或其补角)为异面直线AB1与BC1所成的角，易求得AB1＝，BC1＝AD1＝，B1D1＝.由余弦定理得cos∠B1AD1＝，故选C.‎ ‎[答案]　C ‎4．(2018·全国卷Ⅱ)如图，在三棱锥P－ABC中，AB＝BC＝2，PA＝PB＝PC＝AC＝4，O为AC的中点．‎ ‎(1)证明：PO⊥平面ABC；‎ ‎(2)若点M在棱BC上，且MC＝2MB，求点C到平面POM的距离．‎ ‎[解]　(1)证明：因为AP＝CP＝AC＝4，O为AC的中点，所以OP⊥AC，且OP＝2.‎ 连接OB，因为AB＝BC＝AC，‎ 所以△ABC为等腰直角三角形，且OB⊥AC，OB＝AC＝2.‎ 由OP2＋OB2＝PB2知，OP⊥OB.‎ 由OP⊥OB，OP⊥AC知PO⊥平面ABC.‎ ‎(2)作CH⊥OM，垂足为H.又由(1)可得OP⊥CH，所以CH⊥平面POM.‎ 故CH的长为点C到平面POM的距离．‎ 由题设可知OC＝AC＝2，CM＝BC＝，∠ACB＝45°.所以OM＝，CH＝＝.‎ 所以点C到平面POM的距离为.‎ ‎1.高考对此部分的命题较为稳定，一般为“一小一大”或“一大”，即一道选择或填空题和一道解答题或一道解答题．‎ ‎2．选择题一般在第3～5题的位置，填空题一般在第14题的位置，多考查线面位置关系的判断，难度较小．‎ ‎3．解答题多出现在第18或19题的位置，考查空间中平行或垂直关系的证明、点到平面的距离及三棱锥体积的计算．‎