- 2021-04-14 发布 |
- 37.5 KB |
- 18页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2019届一轮复习北师大版算法初步、推理与证明、复数学案
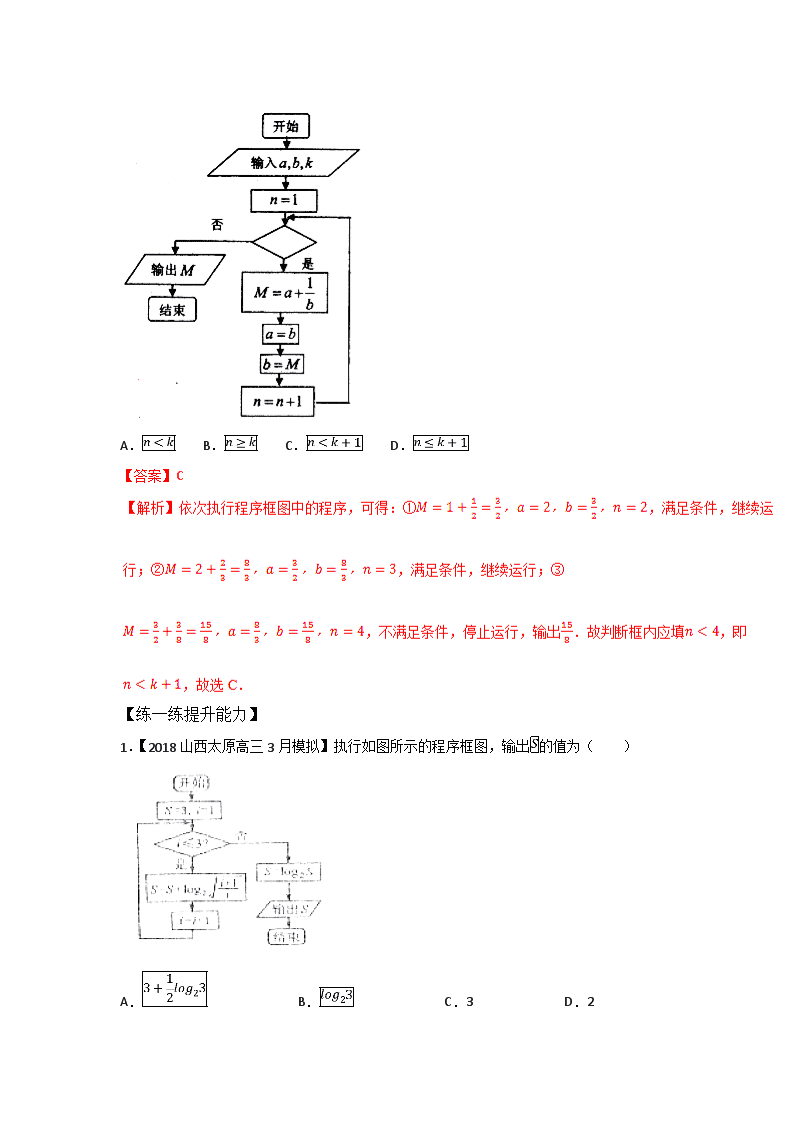
第十三章 算法初步、推与证明、复数 程序框图 【背一背重点知识】 1.算法的定义 算法是指按照 一定规则解决某一类问题的明确和有限的步骤. 2.程序框图 (1)程序框图又称 流程图,是一种用规定的程序、流程线及文字说明 准确、直观地表示算法的图形. (2)程序框图通常由程序框和流程线组成. (3)基本的程序框有终端框(起止框) 、输入、输出框 、处框(执行框) 、判断框. 3.三种基本逻辑结构 顺序结构 由若干个依次执行的步骤组成的,这是任何一个算法都离不开的基本结构 条件结构 算法的流程根据条件是否成立 有不同的流向,条件结构就是处这种过程的结构 循环结构 从某处开始,按照一定的条件反复执行某些步骤的情况,反复执行的步骤称为循环体 【讲一讲提高技能】 1. 必备技能 (1)控制循环结构的是计数变量和累加变量的变化规律以及循环结束的条件.在解答这类题目时首先要弄清楚这两个变量的变化规律,其次要看清楚循环结束的条件,这个条件由输出要求所决定,看清楚是满足条件时结束还是不满足条件时结束. (2)条件结构的程序框图中对判断条件的分类是逐级进行的,其中没有遗漏也没有重复,在解题时对判断条件要仔细辨别,看清楚条件和函数的对应关系,对条件中的数值不要漏掉也不要重复了端点值. 2. 典型例题 例1.【2018河北石家庄高三教 质量检测(二)】我国魏晋期间的伟大的数 家刘徽,是最早提出用逻辑推理的方式 论证数 命题的人,他创立了“割圆术”,得到了著名的“徽率”,即圆周率精确到小数点后两位的近似值 ,如图就是利用“割圆术”的思想设计的一个程序框图,则输出的值为( )(参考数据 ,,) A.24 B.36 C.48 D.12 【答案】C 【易错点睛】应用循环结构应注意的三个问题分别为 (1)确定循环变量和初始值;(2)确定算法中反复执行的部分,即循环体;(3)确定循环的终止条件.同时依次计算出每次的循环结果,直到不满足循环条件为止是解答此类问题的常用方法. 例2.【2018广东六校(广州二中,深圳实验,珠海一中,中山纪念,东莞中 ,惠州一中)高三下 期第三次联考】执行下面的程序框图,如果输入的分别为1,2,3,输出的,那么,判断框中应填入的条件为( ) A. B. C. D. 【答案】C 【练一练提升能力】 1.【2018山西太原高三3月模拟】执行如图所示的程序框图,输出的值为( ) A. B. C.3 D.2 【答案】D 【解析】,所以,故选D. 2.【2018甘肃高三第一次诊断性考试】如图所示,若程序框图输出的所有实数对所对应的点都在函数的图象上,则( ) A. B. C. D. 【答案】B 【解析】执行程序框图 ,是,输出(1,1);,是,输出(2,2);,是,输出(3,4);,否,结束循环.根据题意函数经过点(1,1),(2,2),(3,4).所以 ,解得 .故选B. 合情推理与演绎推理 【背一背重点知识】 1.合情推是根据已有的事实和正确的结论(包括定义、公、定等),实验和实践的结果,以及个人的经验和直觉等推测某些结果的推过程,归纳和类比是合情推常见的方法,在解决问题的过程中,合情推具有猜测和发现结论、探索和提供思路的作用,有利于创新意识的培养. 2.演绎推是指如果推是从一般性的原出发,推出某个特殊情况下的结论,我们把这种推称为演绎推. 演绎推的一般模式是“三段论”,包括 ①大前提;②小前提;③结论. 3.证明方法 (1)直接证明 ①综合法 一般地,利用已知条件和某些数 定义、定、公等,经过一系列的推论证,最后推导出所要证明的结论成立,这种证明方法叫综合法.综合法又叫顺推法或由因导果法. ②分析法 一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定、公等),这种证明方法叫分析法.分析法又叫逆推法或执果索因法. (2)间接证明——反证法 一般地,假设原命题不成立,经过正确的推,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这种证明方法叫反证法. (3)数 归纳法 一般地,证明一个与正整数n有关的命题,可按下列步骤进行 ①(归纳奠基)证明当n取第一个值n0 (n0∈N )时命题成立; ②(归纳递推)假设n= ( ≥n0, ∈N )时命题成立,证明当n= +1时命题也成立. 只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.上述证明方法叫做数 归纳法. 【讲一讲提高技能】 1.必备技能 A.归纳推的一般步骤是 (1)通过观察个别情况发现某些相同的性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想). B.类比推是由特殊到特殊的推,其一般步骤是 (1)找出两类事物之间的相似性或一致性; (2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想). 类比是根据两个不同的对象,在某些方面(如特征、属性、关系等)的类同之处,猜测这两个对象在其他方面也可能有类同之处,并作出某种判断的推方法.类比是 研究最普遍的方法之一.在数 中,类比是发现概念、方法、定和公式的重要手段,也是开拓新领域和创造新分支的重要手段.类比在数 中应用广泛.数与式、平面与空间、一元与多元、低次与高次、相等与不等、有限与无限之间有不少结论,都是先用类比法猜想,而后加以证明的. 类比推的关键是找到合适的类比对象,如上例中的椭圆类比到双曲线,常见的平面几何中的一些定、公式、结论等,可以类比到立体几何中,得到类似的结论.一般平面中的一些元素与空间中的一些元素的类比如表所示 平面 空间 点 线 线 面 圆 球 三角形 三棱锥 角 二面角 面积 体积 周长 表面积 …… …… C.演绎推是由一般性的命题推出特殊性命题的一种推模式,是一种必然性推.演绎推的前提与结论之间有蕴含关系,因而,只要前提是真实的,推的形式是正确的,那么结论必定是真实的,但是错误的前提可能导致错误的结论. 演绎推的主要形式,就是由大前提、小前提推出结论的三段论式推.用集合论的观点 讲,就是 若集合M的所有元素都具有性质P,S是M的子集,那么S中所有元素都具有性质P. D.合情推推出的结论不一定正确,有待进一步证明,演绎推在大前提、小前提和推形式都正确的前提下得到的结论一定正确. 2.典型例题 例1.【2018江西南昌高三一模】平面内直角三角形两直角边长分别为,则斜边长为,直角顶点到斜边的距离为,空间中三棱锥的三条侧棱两两垂直,三个侧面的面积分别为,类比推理可得底面积为,则三棱锥顶点到底面的距离为( ) A. B. C. D. 【答案】C 【名师点睛】类比推理是由特殊到特殊的推理,是两类类似的对象之间的推理,其中一个对象具有某个性质,则另一个对象也具有类似的性质.在进行类比时,要充分考虑已知对象性质的推理过程,然后类比推导类比对象的性质.类比推理时要尽量从本质上去类比,不要被表面现象迷惑,否则会犯机械类比的错误. 例2.【2018四川成都七中高三上 期一诊模拟】在直角坐标平面上的一列点简记为若由构成的数列满足其中为方向与轴正方向相同的单位向量,则称为点列.有下列说法 ①为点列; ②若为点列,且点在点的右上方.任取其中连续三点则可以为锐角三角形; ③若为点列,正整数若,满足则 ④若为点列,正整数若,满足则. 其中,正确说法的个数为() A.1 B.2 C.3 D.4 【答案】C 【解析】①由题意可知,,显然有是 点列,①正确;②在中,,,点在点的右上方,为点列,,,则,为钝角,为钝角三角形,不可以为锐角三角形,②错; ③,, ,③正确; ④同理②, 由于为点列,于是,可推导,,即,④正确,正确说法的个数为,故选C. 【思路点晴】演绎推理是由一般到特殊的推理,数 的证明过程主要是通过演绎推理进行的,只要采用的演绎推理的大前提、小前提和推理形式是正确的,其结论一定是正确,一定要注意推理过程的正确性与完备性. 【练一练提升能力】 1.【2018山东淄博部分 校高三12月摸底考试】《聊斋志异》中有这样一首诗 “挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术” ,,则按照以上规律,若具有 “穿墙术”,则n= A.35 B.48 C.63 D.80 【答案】C 【解析】根据规律得,所以,选C. 2.【2018吉林乾安县第七中 高三上 期第三次模拟考试】 在一次体育兴趣小组的聚会中,要安排人的座位,使他们在如图所示的个椅子中就坐,且相邻座位(如与,与)上的人要有共同的体育兴趣爱好.现已知这人的体育兴趣爱好如下表所示,且小林坐在号位置上,则号位置上坐的是( ) 小林 小方 小马 小张 小李 小周 体育兴趣爱好 篮球, 球,羽毛球 足球,排球,跆拳道 篮球,棒球,乒乓球 击剑, 球,足球 棒球,排球,羽毛球 跆拳道,击剑,自行车 A.小方 B.小张 C.小周 D.小马 【答案】A 【解析】重新整理,篮球 小林,小马; 球 小林,小张; 羽毛球 小林,小李; 足球 小方,小张; 排球 小方,小李; 跆拳道 小方,小周; 棒球 小马,小李; 击剑 小周,小张 乒乓球 小马; 自行车 小周 由于小周的自行车与小马的乒乓球没有共同兴趣爱好者,所以小周两边一事实上是跆拳道与击剑的,小马两边只能是棒球与篮球的.即小马与小林一定相邻,所以1号位是小林,2 号位一定是小马,3号位就是棒球的小李.小周与小张及小方一定相邻,所以小周坐5号位. 从3号位角度,4号位只能是排球和羽毛球(小林,不可能),所以是排球小方.6号位小张.选A. 1 2 3 4 5 6 1 小林 小马 小李 小方 小周 小张 小林 复数的概念、四则运算 【背一背重点知识】 1.复数的有关概念 (1)复数的概念 形如的数叫复数,其中分别是它的实部和虚部.若,则为实数,若,则为虚数,若,则为纯虚数. (2)复数相等 ⇔(). (3)共轭复数 与共轭⇔,() (4)复数的模 向量的模叫做复数的模,记作或,即==. 2.复数的几何意义 (1)复平面的概念 建立直角坐标系 表示复数的平面叫做复平面. (2)实轴、虚轴 在复平面内,轴叫做实轴,轴叫做虚轴,实轴上的点都表示实数;除原点以外,虚轴上的点都表示纯虚数. (3)复数的几何表示 复数复平面内的点平面向量. 3.复数的运算 (1)复数的加、减、乘、除运算法则 (2)复数加法的运算定律 复数的加法满足交换律、结合律. 【讲一讲提高技能】 1必备技能 (1)复数的概念 对于复数a+bi(a,b∈R),a叫做实部,b叫做虚部;当且仅当b=0时,复数a+bi(a,b∈R)是实数a;当b≠0时,复数a+bi叫做虚数;当a=0且b≠0时,复数a+bi叫做纯虚数. (2)复数的运算法则与实数运算法则相同,主要是除法法则的运用,另外复数中的几个常用结论应记熟 (1)(1±i)2=±2i;(2) ;;(3)i4n=1;i4n+1=i;i4n+2=-1;i4n+3=-i; i4n+i4n+1+i4n+2+i4n+3=0;(4)设ω=,则ω0=1;ω2=;ω3=1;1+ω+ω2=0. 2典型例题 例1.【2018河北石家庄高三教 质量检测(二)】已知复数满足,若的虚部为,则复数在复平面内对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【答案】A 【解析】,虚部为,即,故对应点在第一象限. 例2.【2018江西金溪一中、余江一中等五市八校高三上 期第一次联考】若,则( ) A. B. C. D. 【答案】D 【解析】 由,则,故选D. 【方法点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如.其次要熟悉复数相关基本概念,如复数的实部为、虚部为、模为、对应点为、共轭为 【练一练提升能力】 1.【2018辽宁凌 市高三毕业班一模】设是虚数单位,若复数是纯虚数,则( ) A. B. C. D. 【答案】B 【解析】是纯虚数,故故选B. 2.【2018江西上饶市高三上 期第一次模拟】已知复数满足,则( ) A.1 B. C. D. 【答案】A 【解析】,则,故选A. (一)选择题(12 5=60分) 1.【2018甘肃高三第一次诊断性考试】如图所示,若程序框图输出的所有实数对所对应的点都在函数的图象上,则pu实数的值依次为( ) A. B. C. D. 【答案】B 【解析】根据框图得到x=1,y=1,输出点(1,1),这个点在函数上,故得到b=0,x=2,y=3,输出(2,3)故得到a=3,b=0.故选B. 2.【2018湖北武汉高中毕业生二月调研】已知是虚数单位,若复数满足,则( ) A.-5 B.5 C. D. 【答案】B 【解析】,所以,又,选B. 3.【2018四川广元高三第一次高考适应性统考】二维空间中,圆的一维测度(周长),二维测度(面积),三维空间中,球的二维测度(表面积),三维测度(体积),应用合情推理,若四维空间中,“超球”的三维测度,则其思维测度W=( ) A. B. C. D. 【答案】A 【解析】由题意得, 二维空间中,二维测度的导数为一维测度;三维空间中,三维测度的导数为二维测度.由此归纳,在四维空间中,四维测度的导数为三维测度,故.选A. 4.【2018湖北武汉高中毕业生二月调研】执行如图所示的程序框图,则输出的值为( ) A.3 B.4 C.5 D.6 【答案】B 【解析】第一次执行循环时,;第二次执行循环时,;第三次执行循环时,;第四次执行循环时,,终止循环,故输出值. 5.【2018山西太原高三3月模拟考试】若复数在复平面内对应的点在第四象限,则实数的取值范围是( ) A. B. C. D. 【答案】A 【解析】 ,所以,选A. 6.【2018山西晋中市高三1月高考适应性调研考试】若执行下图所示的程序,输出的结果为,则判断框中应填入的条件为( ) A. B. C. D. 【答案】C 7.【2018湖南五市十校教研教改共同体高三12月联考】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第代“勾股树”所有正方形的面积的和为( ) A. B. C. D. 【答案】D 【解析】最大的正方形面积为1,当n=1时,由勾股定理知正方形面积的和为2,依次类推,可得所有正方形面积的和为,选D. 8.【2018山东淄博高三3月模拟考试】在复平面内,复数满足,则对应的点位于 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【答案】B 【解析】∵,∴,∴,故对应的点在第二象限.故选B. 9.【2018山西高三名校模拟考试第一次五校联考】某次夏令营中途休息期间,3位同 根据胡老师的口音对她是哪个地方的人进行了判断 甲说胡老师不是上海人,是福州人; 乙说胡老师不是福州人,是南昌人; 丙说胡老师既不是福州人,也不是广州人. 听完以上3人的判断后,胡老师笑着说,你们3人中有1人说的全对,有1人说对了一半,另一人说的全不对,由此可推测胡老师( ) A.一定是南昌人 B.一定是广州人 C.一定是福州人 D.可能是上海人 【答案】D 【解析】在A中,若胡老师是南昌人,则甲说的全不对,乙说对了一半,丙说的全对,满足条件,故胡老师有可能是南昌人,但不能说一定是南昌人,故A错误;在B中,若胡老师是广州人,则甲说的全不对,乙说的全不对,丙说的全对,不满足条件,故B错误;在C中,若胡老师是福州人,则甲说对一半,乙说的全不对,丙说的全不对,不满足条件,故C错误;在D中,若胡老师是上海人,由甲说的对一半,乙说的全不对,丙说的全对,满足条件,故D正确. 10.【2018安徽马鞍山、含山高三联考】已知表示正整数的所有因数中最大的奇数,例如 12的因数有1,2,3,4,6,12,则;21的因数有1,3,7,21,则,那么的值为( ) A.2488 B.2495 C.2498 D.2500 【答案】D 【解析】由的定义知,且若为奇数则,则 , ,故选D. 11.【2018广东珠海一中等六校高三第三次联考】已知 为虚数单位),又数列满足 当时,;当,为的虚部,若数列的前项和为,则( ) A. B. C. D. 【答案】C 【解析】,∴,又, ∴, , ,故选C. 12.【2018贵州省铜仁一中高三模拟】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本 ”图.下列数表的构造思路就 于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( ) A. B. C. D. 【答案】B (二)填空题(4 5=20分) 13.【2018吉林长春高三质量监测(二)】更相减损术是出自《九章算术》的一种算法.如图所示的程序框图是根据更相减损术写出的,若输入,则输出的值为_____. 【答案】13 【解析】输入,执行程序框图,第一次;第二次;第三次;第四次,满足输出条件,输出的的值为,故答案为. 14.【2018广东华南师大附中高三综合测试(三)】已知为虚数单位,复数满足,则__________. 【答案】2 【解析】,,所以. 15.【2018东北三省三校(哈师大附中、东北师大附中、辽宁省实验中 )高三第一次模拟】甲、乙、丙三位教师分别在哈尔滨、长春、沈阳的三所中 里教不同的 、、,已知 ①甲不在哈尔滨工作,乙不在长春工作;②在哈尔滨工作的教师不教 ; ③在长春工作的教师教 ;④乙不教 . 可以判断乙教的 是______________. 【答案】C 【解析】由乙不在长春工作,而在长春工作的教师教A ,则乙不教A ;又乙不教B ,所以乙教C ,而在哈尔滨工作的教师不教C ,故乙在沈阳教C .故填C. 16.【2018山西晋城高三一模】由1,7,9三个数字组合成一个四位数(其中数字9是重复的),这个四位数有如下信息 (1)与四位数1799有且只有两个位置的数字是相同的;(2)与四位数7991有且只有一个位置的数字是相同的,则满足信息的四位数是__________. 【答案】1979 【解析】由信息(1)列举出满足条件的所有可能的四位数,共有五种,分别是 1997,1979,9791,9719,7199. 若这个数是1997,则与7991有两个位置的数字相同,与信息(2)矛盾;若这个数是1979,则满足信息(2);若这个数是9791,则与7991有两个位置的数字相同,与信息(2)矛盾;若这个数是9719,则与7991四个个位置的数字均不同,与信息(2)矛盾;若这个数是7199,则与7991有两个位置的数字相同,与信息(2)矛盾. = 综上可得这个四位数只能是1979.查看更多