- 2021-04-14 发布 |
- 37.5 KB |
- 38页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考文科数学复习备课课件:第二节 算法与程序框图
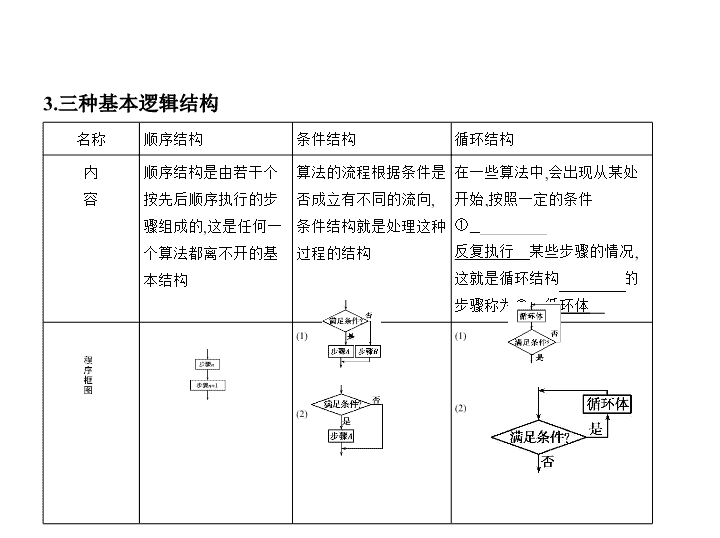
文数 课标 版 第二节 算法与程序框图 2.程序框图 (1)程序框图又称流程图,是一种用程序框、流程线及文字说明来表示 算法的图形. (2)基本的程序框有终端框(起止框),输入、输出框,处理框(执行框),判断 框. 1.算法的定义 算法通常是指按照一定规则解决某一类问题的明确和有限的步骤. 教材研读 3.三种基本逻辑结构 名称 顺序结构 条件结构 循环结构 内 容 顺序结构是由若干个按先后顺序执行的步骤组成的,这是任何一 个算法都离不开的基本结构 算法的流程根据条件是否成立有不同的流向,条件结构就是处理这种过程的结构 在一些算法中,会出现从某处开始,按照一定的条件 ① 反复执行 某些步骤的情况,这就是循环结构,反复执行的步骤称为② 循环体 (1) (2) (1) (2) 4.基本算法语句 (1)输入、输出、赋值语句的一般格式与功能 语句 一般格式 功能 输入语句 ③ INPUT “提示内容”;变 输入信息 输出语句 ④ PRINT “提示内容”;表达式 输出常量、变量的值和系统信息 赋值语句 ⑤ 变量=表达式 将表达式的值赋给变量 (2)条件语句的格式及框图 a.IF-THEN格式 b.IF-THEN-ELSE格式 (3)循环语句的格式及框图 a.UNTIL语句 b.WHILE语句 判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)算法的每一步都有确定的意义,且可以无限地运算. ( × ) (2)一个程序框图一定包含顺序结构,也包含条件结构和循环结构. ( × ) (3)一个循环结构一定包含条件结构. (√) (4)5= x 是赋值语句. ( × ) (5)输入语句可以同时给多个变量赋值. (√) 1.执行如图所示的程序框图,若输入 x =2,则输出的 y 值为 ( ) A.0 B.1 C.2 D.3 答案 B ∵2>0,∴ y =2 × 2-3=1. 2.(2016北京,3,5分)执行如图所示的程序框图,输出的 s 值为 ( ) A.8 B.9 C.27 D.36 答案 B 由题意,知 这时3>2,输出 s =9,故选B. 3.阅读下边的程序框图,运行相应的程序,则输出 S 的值为 ( ) A.-10 B.6 C.14 D.18 答案 B 由题意知: i =2, S =20-2=18; i =4, S =18-4=14; i =8, S =14-8=6,满足 i > 5的条件,结束循环,输出 S 的值为6,故选B. 4.执行如图所示的程序框图,则输出的 k 的值是 . 答案 6 解析 由不等式 k 2 -6 k +5>0可得 k >5或 k <1,所以执行程序框图可得 k =6. 5.某程序框图如图所示,则该程序运行后输出的值是 . 答案 解析 由程序框图可知: T =1, i =2; T = , i =3; T = , i =4; T = , i =5; T = , i =6. 此时 i =6>5,输出 T ,所以输出的值为 . 考点一 程序框图的应用 典例1 (1)(2016福建福州五校联考)定义[ x ]为不超过 x 的最大整数,例如 [1.3]=1.执行如图所示的程序框图,当输入的 x 为4.7时,输出的 y 值为( ) 考点突破 A.7 B.8.6 C.10.2 D.11.8 (2)(2016课标全国Ⅰ,10,5分)执行下面的程序框图,如果输入的 x =0, y =1, n =1,则输出 x , y 的值满足 ( ) A. y =2 x B. y =3 x C. y =4 x D. y =5 x (3)(2015课标Ⅱ,8,5分)下边程序框图的算法思路源于我国古代数学名 著《九章算术》中的“更相减损术”.执行该程序框图,若输入的 a , b 分 别为14,18,则输出的 a = ( ) A.0 B.2 C.4 D.14 答案 (1)C (2)C (3)B 解析 (1)当输入的 x 为4.7时,执行程序框图可知,4.7-[4.7]=0.7,即4.7-[4.7] 不等于0,因而可得 y =7+([4.7-3]+1) × 1.6=10.2,输出的值为10.2.故选C. (2)执行程序框图:当 n =1时, x =0, y =1,此时0 2 +1 2 ≥ 36不成立;当 n =2时, x = , y =2,此时 +2 2 ≥ 36不成立;当 n =3时, x = , y =6,此时 +6 2 ≥ 36成立,结 束循环,输出 x 的值为 , y 的值为6,满足 y =4 x ,故选C. (3)执行程序框图:当 a =14, b =18时, a < b ,则 b =18-14=4; 当 a =14, b =4时, a > b ,则 a =14-4=10; 当 a =10, b =4时, a > b ,则 a =10-4=6; 当 a =6, b =4时, a > b ,则 a =6-4=2; 当 a =2, b =4时, a < b ,则 b =4-2=2, 此时 a = b =2,输出 a 为2,故选B. 易错警示 执行循环结构首先要分清是先执行循环体,再判断条件,还是先判断条 件,再执行循环体;其次注意控制循环的变量是什么,何时退出循环;最后 要清楚循环体内的程序是什么,是如何变化的. 1-1 (2016课标全国Ⅱ,9,5分)中国古代有计算多项式值的秦九韶算法, 下图是实现该算法的程序框图.执行该程序框图,若输入的 x =2, n =2,依次 输入的 a 为2,2,5,则输出的 s = ( ) A.7 B.12 C.17 D.34 答案 C 执行程序框图,输入 a 为2时, s =0 × 2+2=2, k =1,此时 k >2不成立; 再输入 a 为2时, s =2 × 2+2=6, k =2,此时 k >2不成立;再输入 a 为5时, s =6 × 2+5= 17, k =3,此时 k >2成立,结束循环,输出 s 为17,故选C. 1-2 (2015课标Ⅰ,9,5分)执行下面的程序框图,如果输入的 t =0.01,则输 出的 n = ( ) A.5 B.6 C.7 D.8 答案 C S =1- = , m = , n =1; S = - = , m = , n =2; S = - = , m = , n =3; S = - = , m = , n =4; S = - = , m = , n =5; S = - = , m = , n =6; S = - = , m = , n =7, 此时不满足 S > t ,结束循环,输出 n 为7,故选C. 1-3 (2014课标Ⅰ,9,5分)执行下面的程序框图,若输入的 a , b , k 分别为1,2, 3,则输出的 M = ( ) A. B. C. D. 答案 D 第一次循环, M = , a =2, b = , n =2; 第二次循环, M = , a = , b = , n =3; 第三次循环, M = , a = , b = , n =4, 此时 n > k ,退出循环,输出 M 为 ,故选D. 考点二 程序框图的完善 典例2 (1)执行如图所示的程序框图,若输出 k 的值为8,则判断框内可填 入的条件是 ( ) A. s ≤ B. s ≤ C. s ≤ D. s ≤ (2)如图给出的是计算 + + … + 的值的一个程序框图,则图中判断框 内和执行框中应填的语句分别是 ( ) A. i >100, n = n +1 B. i >100, n = n +2 C. i >50, n = n +2 D. i ≤ 50, n = n +2 A.20 B.21 C.22 D.23 答案 (1)C (2)C (3)A 解析 (1) k =2, s = ; k =4, s = + = ; (3)(2016安徽合肥模拟)执行如图所示的程序框图,如果输出的 k 的值为3, 则输入的 a 的值可以是 ( ) k =6, s = + + = ; k =8, s = + + + = . 此时循环结束,所以判断框中可填入的条件是 s ≤ ,选C. (2)因为 , , … , 共50个数,所以程序框图应运行50次,所以变量 i 应满 足 i >50,因为是求偶数的倒数和,所以应使变量 n 满足 n = n +2,故选C. (3)根据程序框图可知,若输出的 k =3,则此时程序框图中的循环结构执行 了3次,执行第1次时, S =2 × 0+3=3,执行第2次时, S =2 × 3+3=9,执行第3次时, S =2 × 9+3=21,因此符合题意的实数 a 的取值范围是9 ≤ a <21.故选A. 方法技巧 解决程序框图填充问题的思路 (1)要明确程序框图的顺序结构、条件结构和循环结构. (2)理解框图所解决的实际问题. (3)按照题目的要求完成解答并验证. 2-1 (2016河南郑州模拟)执行如下程序框图,若输出的结果为273,则判 断框内应补充的条件为 ( ) A. i >7 B. i ≥ 7 C. i >9 D. i ≥ 9 答案 B 由程序框图可知: S =0+3 1 =3, i =3; S =3+3 3 =30, i =5; S =30+3 5 =273, i =7.故判断框内可填 i ≥ 7,故选B. 2-2 某程序框图如图所示,若该程序运行后输出的值是 ,则 ( ) A. a =3 B. a =4 C. a =5 D. a =6 答案 A 第1次循环, S =1+ = , k =1+1=2,继续循环; 第2次循环, S = + = , k =2+1=3,继续循环; 第3次循环, S = + = , k =4,符合条件,输出 S 的值. 所以判断框内的条件是 k >3,故 a =3,选A. 考点三 基本算法语句 典例3 根据如图所示的算法语句,可知输出的结果 S 为 . S=1 I=1 While I<8 S=S+2 I=I+3 End While Print S 答案 7 解析 S =1, I =1,1<8; S =3, I =4,4<8; S =5, I =7,7<8; S =7, I =10, ∵10>8,∴循环结束,输出 S =7. 方法技巧 解决算法语句的有关问题有三个步骤:首先通读全部语句,把它翻译成 数学问题;其次领悟这些语句的功能;最后根据语句的功能运行程序,解 决问题. 3-1 运行下面的程序,输出的结果为 ( ) n=10 S=100 DO S=S-n n=n-1 LOOP UNTIL S<=70 PRINT n END A.4 B.5 C.6 D.7 答案 C 程序运行过程如下: n =10, S =100; S =100-10=90, n =10-1=9; S =90-9=81, n =9-1=8; S =81-8=73, n =8-1=7; S =73-7=66, n =7-1=6, 此时 S =66<70,结束循环,输出 n =6. 3-2 执行下边的程序,输出的结果是 . S=1 i=3 WHILE S<=200 S=S*i i=i+2 WEND PRINT i END 答案 11 解析 根据循环结构可得, S =1 × 3=3, i =3+2=5; S =3 × 5=15, i =5+2=7; S =15 × 7=105, i =7+2=9; S =105 × 9=945, i =9+2=11,945>200,则结束循环,输出 i =11.查看更多