2005年河南省高考数学试卷Ⅰ(文)【附答案、word版本,可再编辑;B4纸型两栏】
2005年河南省高考数学试卷Ⅰ(文)
一、选择题(共12小题,每小题5分,满分60分)
1. 设直线l过点(-2, 0),且与圆x2+y2=1相切,则l的斜率是( )
A.±1 B.±12 C.±33 D.±3
2. 设I为全集,S1、S2、S3是I的三个非空子集,且S1∪S2∪S3=I,则下面论断正确的是( )
A.∁IS1∩(S2∪S3)=⌀ B.S1⊆(∁IS2∩∁IS3)
C.∁IS1∩∁IS2∩∁IS3=⌀ D.S1⊆(∁IS2∪∁IS3)
3. 用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )
A.8π3 B.82π3 C.82π D.32π3
4. 函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a=( )
A.2 B.3 C.4 D.5
5. 如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF // AB,EF=2,则该多面体的体积为( )
A.23 B.33 C.43 D.32
6. 已知双曲线x2a2-y2=1(a>0)的一条准线为x=32,则该双曲线的离心率为( )
A.32 B.32 C.62 D.233
7. 当0
-2x的解集为(1, 3).
第9页 共12页 ◎ 第10页 共12页
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求a的取值范围.
20. 9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为0.5,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种.
(1)求甲坑不需要补种的概率;
(2)求有坑需要补种的概率.(精确到0.001)
21. 设正项等比数列{an}的首项a1=12,前n项和为Sn,且210S30-(210+1)S20+S10=0.
(1)求{an}的通项;
(2)求{nSn}的前n项和Tn.
22. 已知椭圆的中心为坐标原点O,焦点在x轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,OA→+OB→与a→=(3, -1)共线.
(I)求椭圆的离心率;
(II)设M为椭圆上任意一点,且OM→=λOA→+μOB→(λ, μ∈R),证明λ2+μ2为定值.
第9页 共12页 ◎ 第10页 共12页
参考答案与试题解析
2005年河南省高考数学试卷Ⅰ(文)
一、选择题(共12小题,每小题5分,满分60分)
1.C
2.C
3.B
4.D
5.A
6.D
7.C
8.B
9.C
10.C
11.B
12.D
二、填空题(共4小题,每小题4分,满分16分)
13.155
14.6
15.100
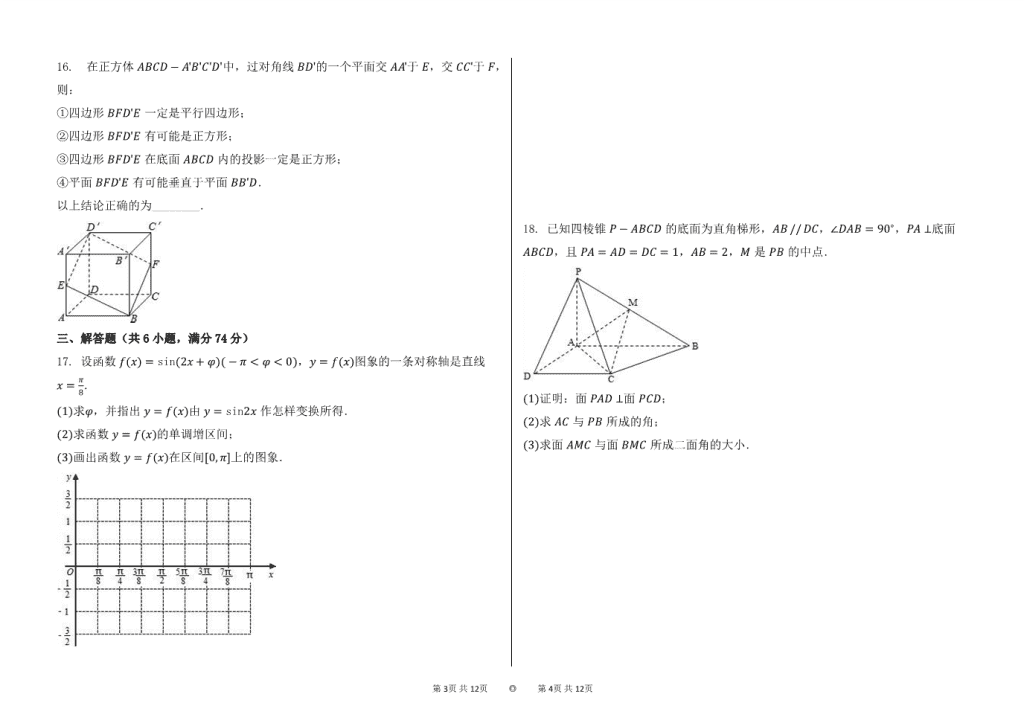
16.①③④
三、解答题(共6小题,满分74分)
17.解:(1)∵ x=π8是函数y=f(x)的图象的对称轴,
∴ sin(2×π8+φ)=±1,
∴ π4+φ=kπ+π2,k∈Z.
∵ -π<φ<0,φ=-3π4.
由y=sin2x向右平移3π8得到.
(2)由(1)知φ=-3π4,因此y=sin(2x-3π4).
由题意得2kπ-π2≤2x-3π4≤2kπ+π2,k∈Z.
所以函数y=sin(2x-3π4)的单调增区间为[kπ+π8,kπ+5π8],k∈Z.
(3)由y=sin(2x-3π4)知
x
0
π8
3π8
5π8
7π8
π
y
-22
-1
0
1
0
-22
故函数y=f(x)在区间[0, π]上图象是
18.(1)证明:如图,
∵ PA⊥面ABCD,CD⊥AD,
第9页 共12页 ◎ 第10页 共12页
∴ 由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴ CD⊥面PAD.
又CD⊂面PCD,
∴ 面PAD⊥面PCD.
(2)解:过点B作BE // CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE=2,又AB=2,
所以四边形ACBE为正方形.由PA⊥面ABCD得∠PEB=90∘
在Rt△PEB中BE=a2=3b2,PB=5,
∴ cos∠PBE=BEPB=105.
∴ AC与PB所成的角为arccos105.
(3)解:作AN⊥CM,垂足为N,连接BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴ △AMC≅△BMC,
∴ BN⊥CM,故∠ANB为所求二面角的平面角
∵ CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN⋅MC=CM2-(AC2)2⋅AC,
∴ AN=32×252=65.
∴ AB=2,
∴ cos∠ANB=AN2+BN2-AB22×AN×BN=-23
故所求的二面角为arccos(-23).
19.解:(1)∵ f(x)+2x>0的解集为(1, 3),
∴ f(x)+2x=a(x-1)(x-3),且a<0.
因而f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a.①
由方程f(x)+6a=0得ax2-(2+4a)x+9a=0.②
因为方程②有两个相等的根,所以Δ=[-(2+4a)]2-4a⋅9a=0,
即5a2-4a-1=0,解得a=1或a=-15.
由于a<0,舍去a=1,故a=-15.
将a=-15代入①得f(x)的解析式f(x)=-15x2-65x-35.
(2)由f(x)=ax2-2(1+2a)x+3a=a(x-1+2aa)2-a2+4a+1a,
及a<0,可得f(x)的最大值为-a2+4a+1a.
由-a2+4a+1a>0a<0解得a<-2-3或-2+30,所以210q10=1,解得q=12,因而an=a1qn-1=12n,n=1,2,.
(2)由题意知Sn=12(1-12n)1-12=1-12n,nSn=n-n2n.
则数列{nSn}的前n项和Tn=(1+2++n)-(12+222++n2n),Tn2=12(1+2++n)-(122+223++n-12n+n2n+1).
前两式相减,得Tn2=12(1+2++n)-(12+122++12n)+n2n+1=n(n+1)4-12(1-12n)1-12+n2n+1即Tn=n(n+1)2+12n-1+n2n-2.
22.解:(1)设椭圆方程为x2a2+y2b2=1(a>b>0),F(c,0)
则直线AB的方程为y=x-c,代入x2a2+y2b2=1,
化简得(a2+b2)x2-2a2cx+a2c2-a2b2=0.
令A(x1, y1),B(x2, y2),
则x1+x2=2a2ca2+b2,x1x2=a2c2-a2b2a2+b2.
∵ OA→+OB→=(x1+x2,y1+y2),a→=(3,-1),OA→+OB→与a→共线,
∴ 3(y1+y2)+(x1+x2)=0,又y1=x1-c,y2=x2-c,
∴ 3(x1+x2-2c)+(x1+x2)=0,
∴ x1+x2=32c.
即2a2ca2+b2=3c2,
所以a2=3b2.
∴ c=a2-b2=6a3,
故离心率e=ca=63.
(II)证明:由(1)知a2=3b2,
所以椭圆x2a2+y2b2=1(a>b>0),F(c,0)可化为x2+3y2=3b2.
设M(x, y),
由已知得(x, y)=λ(x1, y1)+μ(x2, y2),
∴ x=λx1+μx2y=λy1+μy2
∵ M(x, y)在椭圆上,
∴ (λx1+μx2)2+3(λy1+μy2)2=3b2.
即λ2(x12+3y12)+μ2(x22+3y22)+2λμ(x1x2+3y1y2)=3b2.①
由(1)知a2=32c2,b2=12c2.
∴ x1+x2=3c2,x1x2=a2c2-a2b2a2+b2=38c2
∴ x1x2+3y1y2=x1x2+3(x1-c)(x2-c)=4x1x2-3(x1+x2)c+3c2=32c2-92c2+3c2=0.
又x12+3y12=3b2,x22+3y22=3b2,
代入①得λ2+μ2=1.
故λ2+μ2为定值,定值为1.
第9页 共12页 ◎ 第10页 共12页