江西省赣州市于都二中2019-2020学年高二上学期第三次月考数学（理）试题 含答案

江西省赣州市于都二中2019-2020学年高二上学期第三次月考数学（理）试题 含答案

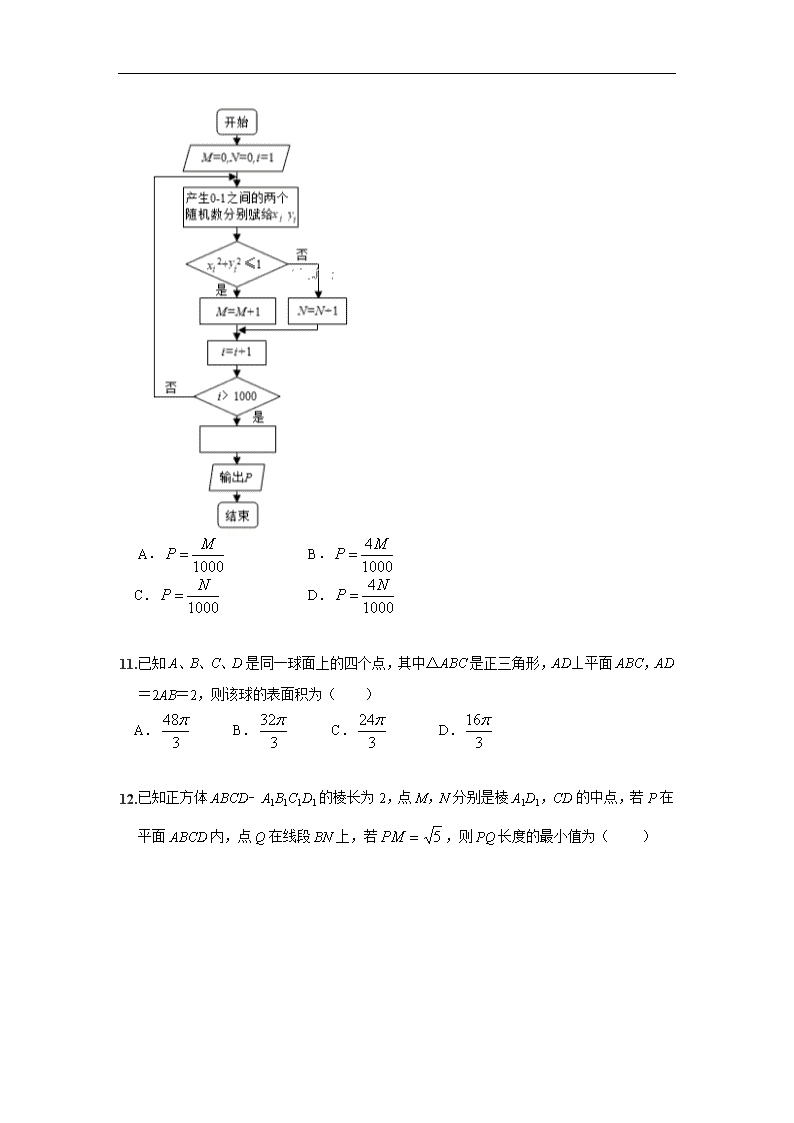
数学（理）试卷 ‎ 第Ⅰ卷（选择题部分，共60分）‎ 一、 选择题：共12小题，每小题5分，共60分.在每个小题给出的四个选项中，只有一项是 符合题目要求的.‎ ‎1.设＝（﹣2，2，t），＝（6，﹣4，5）分别是平面α，β的法向量．若α⊥β，则实数t的值是（　 　）‎ ‎ A．6 B．5 C．4 D．3‎ ‎2.若两个向量，则平面ABC的一个法向量为（　 　）‎ A．（﹣1，2，﹣1） B．（﹣1，2，1） C．（1，2，﹣1） D．（1，2，1）‎ ‎3.如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果，根据扇形统计图可以知道丙、丁两组人数之和为（ ）‎ A.150 B.250 C. 300 D. 400‎ ‎4.盒子中有若干个红球和黄球，已知从盒中取出2个球都是红球的概率为，从盒中取出2个球都是黄球的概率是，则从盒中任意取出2个球恰好是同一颜色的概率是（ ）‎ A. B. C. D. ‎ ‎5.若向量，则“x=4”是的 （　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎6.‎ 把12人平均分成两组，再从每组里任意指定正、副组长各一人，其中甲被指定为正组长的概率是( 　)‎ ‎ A． B． C． D． ‎7.下列命题中正确的是（　 ）‎ A．对于任意两个事件A和B，都有P(A+B)= P(A)+ P(B) ‎ B．若随机事件A发生的概率为P(A)，则0≤ P(A) ≤1 ‎ C．命题“若平面向量共线，则方向相同”的逆否命题为真命题 ‎ D．命题“若a+b≥4，则a、b中至少有一个大于2”的逆命题是真命题．‎ ‎8.设a、b是两条不同的直线，α、β是两个不同的平面，则下列命题中正确的是(　　)‎ A．若a∥b，a∥α，则b∥α B．若α⊥β，a∥α，则a⊥β C．若α⊥β，a⊥β，则a∥α D．若a⊥b，a⊥α，b⊥β，则α⊥β ‎9.一个多面体的直观图和三视图所示，是的中点，一只蝴蝶在几何体内自由飞翔，则它飞入几何体内的概率为（ ）‎ ‎ A. B. C. D. ‎ ‎10.如图是用模拟方法估计圆周率π值的程序框图，P表示估计结果，‎ 则图中空白框内应填入（　 　）‎ A． ‎ B． ‎ ‎ C． D．‎ ‎11.已知A、B、C、D是同一球面上的四个点，其中△ABC是正三角形，AD⊥平面ABC，AD＝2AB＝2，则该球的表面积为（　　）‎ A． B． C． D．‎ ‎12.已知正方体ABCD﹣A1B1C1D1的棱长为2，点M，N分别是棱A1D1，CD的中点，若P在平面ABCD内，点Q在线段BN上，若，则PQ长度的最小值为（　 　）‎ A． B． C． D．‎ 第Ⅱ卷（非选择题部分，共90分）‎ 二、填空题：本大题共4小题，每小题5分,共20分.‎ ‎13.已知向量分别是直线l和平面α的方向向量和法向量，若cos〈〉＝－，则l与α所成的角为　 　． ‎ ‎14. 已知5个正整数，它们的平均数是4，众数是3，5，则这5个数的方差为　 　．‎ ‎15.如图，在棱长为1的正四面体PABC中，点A在侧面PBC内的投影为O，则O到底面ABC的距离为_________．‎ ‎16.如图，四边形ABCD和ADPQ均为正方形，他们所在的平面互相垂直， 动点M在线段PQ上，E、F分别为AB、BC的中点，设异面直线EM与AF所成的角为θ，则cosθ的最大值为　 　． ‎ 三、解答题：本大题共6小题，共70分. 解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（本小题满分10分）‎ ‎ 设命题p：实数x满足（x﹣a）（x﹣2a）＜0，其中a＞0；‎ ‎ 命题q：实数x满足（2x﹣16）（2x﹣2）≤0．‎ ‎（1）若a＝1，p，q都是真命题，求实数x的取值范围；‎ ‎（2）若p是q的充分不必要条件，求实数a的取值范围．‎ 18. ‎（本小题满分12分）‎ 一个盒子里装有三张卡片，分别标记有数字1、2、3，这三张卡片除标记的数字外完全相同．随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a、b、c．‎ ‎（1）求“抽取的卡片上的数字满足a+b＝c”的概率；‎ ‎（2）求“抽取的卡片上的数字a、b、c不完全相同”的概率．‎ ‎19.（本小题满分12分）‎ 某班20名学生某次数学考试成绩（单位：分）的频率分布直方图如图所示：‎ ‎（1）求频率分布直方图中实数a的值；‎ ‎（2）估计20名学生成绩的平均数；‎ ‎（3）从成绩在[50，70）的学生中任选2人，求此2人的成绩不都在[60，70）中的概率．‎ ‎20.（本小题满分12分）‎ 如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD＝DC=AD，点E是PC的中点．‎ ‎（1）求证：PA∥平面BDE；‎ ‎（2）求直线BD与平面PBC所成角的大小．‎ ‎21. （本小题满分12分）‎ ‎2015年12月，华中地区多个城市空气污染指数“爆表”，此轮污染为2015年以来最严重的污染过程，为了探究车流量与的浓度是否相关，现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与的数据如表：‎ 时间 星期一 星期二 星期三 星期四 星期五 星期六 星期日 车流量x（万辆）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 的浓度（微克/立方米）‎ ‎28‎ ‎30‎ ‎35‎ ‎41‎ ‎49‎ ‎56‎ ‎62‎ ‎（1）由散点图知与x具有线性相关关系，求关于x的线性回归方程；（提示数据： ）‎ ‎（2）（I）利用（1）所求的回归方程，预测该市车流量为12万辆时的浓度；‎ ‎（II）规定：当一天内的浓度平均值在内，空气质量等级为优；当一天内的浓度平均值在 内，空气质量等级为良，为使该市某日空气质量为优或者为良，则应控制当天车流量不超过多少万辆？（结果以万辆为单位，保留整数）参考公式：回归直线的方程是，其中， .‎ ‎22. （本小题满分12分）‎ 已知正方体中，点是四边形内（含边界）任意一点， 是中点.‎ ‎（1）求证：AC⊥BP；‎ ‎（2）当CQ⊥AP且AP与平面ABCD所成角的正弦值为时， ‎ 求二面角P-AD-C的余弦值．‎ 数学（理）试卷 答案 ‎1-12:C A B A A B B D C B D C ‎ ‎ 13．30° 14． 15． 16．‎ ‎12解：如图，取AD中点O，则MO⊥面ABCD，即MO⊥OP，‎ ‎∵PM＝，∴OP＝＝1，‎ ‎∴点P在以O为圆心，1以半径的位于平面ABCD内的半圆上．‎ 可得O到BN的距离减去半径即为PQ长度的最小值，‎ 作OH⊥BN于H，△BON的面积为：S△BON＝2×2﹣＝，‎ ‎∴＝＝，解得OH＝，‎ ‎∴PQ长度的最小值为：OH﹣OP＝＝．故选：C．‎ ‎17.解：（1）当a＝1时，（x﹣1）（x﹣2）＜0解得1＜x＜2，………………1分 ‎（2x﹣16）（2x﹣2）≤0解得2≤2x≤16，即1≤x≤4，………………2分 所以当p，q都是真命题时，解得1＜x＜2，………………4分 故实数x的取值范围为（1，2）；………………5分 ‎（2）命题p：a＜x＜2a，因为p是q的充分不必要条件，所以（a，2a）⫋[1，4]，………………7分 ‎，解得1≤a≤2，………………9分 故实数a的取值范围为[1，2]．………………10分 ‎18.【解答】解：（Ⅰ）所有的可能结果（a，b，c）共有27种，‎ 而满足a+b＝c的（a，b，c）有（1，1，2）、（1，2，3）、（2，1，3），共计3个，‎ 故“抽取的卡片上的数字满足a+b＝c”的概率为＝．………………6分 ‎（Ⅱ）满足“抽取的卡片上的数字a，b，c完全相同”的（a，b，c）有：‎ ‎（1，1，1）、（2，2，2）、（3，3，3），共计三个，‎ 故“抽取的卡片上的数字a，b，c完全相同”的概率为＝，‎ ‎∴“抽取的卡片上的数字a，b，c不完全相同”的概率为1﹣＝．………………12分 ‎19.解：（1）由（0.2a+0.3a+0.7a+0.6a+0.2a）×10＝1，解得a＝；………………2分 ‎（2）20名学生的平均成绩估计为：（0.2×55+0.3×65+0.7×75+0.6×85+0.2×95）×10×＝76.5分；‎ ‎………………………………………………………………………………………………………………6分 ‎（3）成绩在[50，70]内的学生共有（0.2+0.3）×10××20＝5人，设为a、b、C、D、E,其中成绩在[60，70]内的有3人，即C、D、E，………………………………8分 从这5人中任选2人，共有（a,b）、（a,C）、（a,D）、（a,E）、（b,C）、（b,D）、（b,E）、（C,D）、（C,E）、（D,E）10种，其中都在[60，70]内的有3种，不都在[60，70]内的有10﹣3＝7种，……………………10分 根据古典概型概率公式得：………………………………12分 ‎20.解：（1）证明：连结AC，BD，交于点O，连结OE，‎ ‎∵底面ABCD是矩形，∴O是AC的中点，‎ ‎∵点E是PC的中点，∴OE∥PA，……………………………2分 ‎∵OE⊂平面BDE，PA⊄平面BDE，‎ ‎∴PA∥平面BDE．……………………………4分 ‎（2）解：∵在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD＝DC，‎ ‎∴以D为原点，DA，DC，DP所在直线分别为x，y，z轴，建立空间直角坐标系，‎ 设PD＝DC＝AD＝2，则B（2，2，0），D（0，0，0），P（0，0，2），C（0，2，0），‎ ‎＝（﹣2，﹣2，0），＝（2，2，﹣2），＝（0，2，﹣2），……………………………7分 设平面PBC的法向量＝（x，y，z），‎ 由有取 ……………………………9分 ‎ 设直线BD与平面PBC所成角为θ，‎ ‎∴，……………………………11分 所以直线BD与平面PBC所成角为30° ……………………………12分 ‎21.解(1)由数据可得： ……………………………1分 ‎ ……………………………2分 ‎， ……………………………4分 ‎，（注:用另一个公式求运算量小些）……………………………5分 故关于的线性回归方程为. ……………………………6分 (2) ‎(ⅰ)当车流量为12万辆时，即时， .……………………………8分 ‎ 故车流量为12万辆时， 的浓度为91微克/立方米.……………………………9分 ‎ (ⅱ)根据题意信息得： ，即， …………………………11分 故要使该市某日空气质量为优或为良，则应控制当天车流量在13万辆以内.…………………12分 22. ‎（1）证明：在正方体中，AC⊥BD，DD1⊥平面ABCD，‎ 则DD1⊥AC 又BD∩DD1=D，‎ 则AC⊥平面 BP⫋‎ ‎∴AC⊥BP……………………………4分 ‎（2）如图以D为原点，DA为x轴，DC为y轴，DD1为z轴建立空间直角坐标系 设AB=2，则A(2,0,0)，C(0,2,0)，Q（1,2,2）‎ 设P（x,y,z），显然x、y、z>0则 ‎∵CQ⊥AP ∴ ∴x=2z-2………………5分 易知，平面ABCD的法向量为………………6分 化简得，故………………8分 设平面PAD的法向量为 由有取 ………………10分 ‎………………11分 ‎∵二面角P-AD-C为锐二面角，‎ ‎∴二面角P-AD-C的余弦值为．………………12分