- 2021-04-13 发布 |
- 37.5 KB |
- 41页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学 数与式 实数及其运算复习
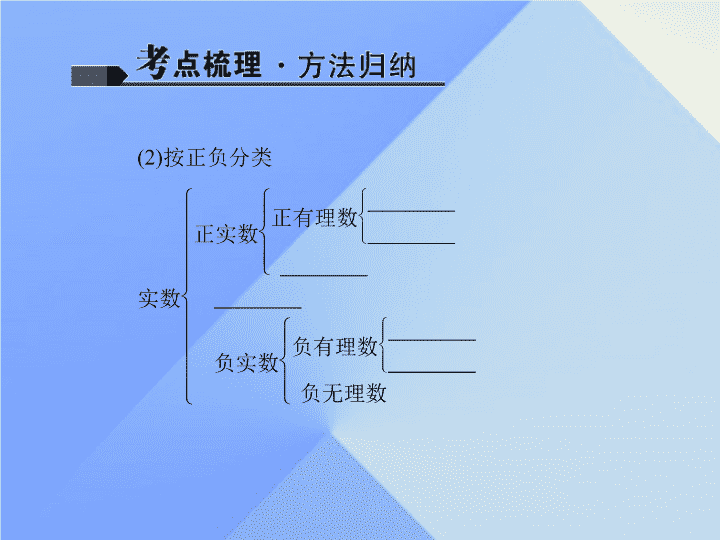
山西省 数学 第1 节 实数及其运算 第一章 数与式 2 . 实数的有关概念 (1) 数轴:规定了 _________ , 和 的直线叫做数轴 , 数轴上所有的点与全体 一一对应. 原点 正方向 单位长度 实数 (2) 相反数:实数 a 的相反数是 _______ , 0 的相反数是 0 ; a 与 b 互为相反数 ⇔ a + b = ______ ; - a 0 距离 a 0 - a ≥ 0 ± a ± b ≥ ≤ ≠ 1 (5) 科学记数法 , 近似数 ① 把数 x 写成 a × 10 n (1 ≤ | a | < 10 , 且 n 为整数 ) 的形式叫做 ______________ . 方法 1 :当 | x | ≥ 1 时 , n 为自然数 , 等于数 x 的整数部分的位数减 ______ ;当 | x | < 1 时 , n 为负整数 , 其绝对值等于数 x 中 _________ 非 0 数字前面所有 0 的个数. 方法 2 : n 的绝对值等于小数点向左或向右移动的位数 , 小数点向右移 , 则 n 为 _________ ;小数点向左移 , 则 n 为 ________ ; ② 一个近似数 , ______________ 到哪一位 , 就说这个数精确到哪一位. 科学记数法 1 从左边起 负数 正数 四舍五入 (6) 平方根、算术平方根、立方根 右 左 小 乘方 开方 乘除 加减 小括号 中括号 大括号 从左往右算 1 2 . 科学记数法中 a 与 n 的确定 科学 记 数法的表示形式 为 a × 10 n 的形式 , 其中 1≤| a | < 10 , n 为 整数. (1) 确定 a : a 是只有一位整数的数 , 即 1 ≤ | a | < 10 ; (2) 确定 n : ① 当原数的 绝对值 ≥ 10 时 , n 是正整数 , n 等于原数的整数位数减去 1 , 或等于原数 变 成 a 时 , 小数点移 动 的位数; ② 当 0 <原数的 绝对值 < 1 时 , n 是 负 整数 , n 的 绝对值 等于原数中左起第一个非零数前零的个数 ( 含整数位数的零 ) ;或 n 的 绝对值 等于原数 变为 a 时 , 小数点移 动 的位数. D 命题点 2 :科学记数法 1 . ( 2011 · 山西 ) 2011 年第一季度 , 我省固定资产投资完成 475.6 亿元 , 这个数据用科学记数法可表示为 ( ) A . 47.56 × 10 9 元 B . 0.4756 × 10 11 元 C . 4.756 × 10 10 元 D . 4.756 × 10 9 元 2 . ( 2012 · 山西 ) 为了实现街巷硬化工程高质量 “ 全覆盖 ” , 山西省 2012 年 1 ~ 4 月公路建设累计投资 92.7 亿元 , 该数据用科学记数法可表示为 ( ) A . 0.927 × 10 10 元 B . 92.7 × 10 8 元 C . 9.27 × 10 11 元 D . 9.27 × 10 9 元 C D 3 . ( 2013 · 山西 ) 起重机将质量为 6.5 t 的货物沿竖直方向提升了 2 m , 则起重机提升货物所做的功用科学记数法表示为 (g = 10 N / kg )( ) A . 1.3 × 10 6 J B . 13 × 10 5 J C . 13 × 10 4 J D . 1.3 × 10 5 J 4 . ( 2014 · 山西 ) PM 2.5 是指大气中直径小于或等于 2.5 μm (1 μm = 0.000 001 m ) 的颗粒物 , 也称为可入肺颗粒物 , 它们含有大量有毒、有害物质 , 对人体健康和大气环境质量有很大危害 , 2.5 μm 用科学记数法可表示为 ( ) A . 2.5 × 10 - 5 m B . 0.25 × 10 - 7 m C . 2.5 × 10 - 6 m D . 25 × 10 - 5 m D C B C 【 点评 】 判断一个数是不是无理数 , 关 键 就看它能否写成无限不循 环 小数 , 掌握常 见 无理数的四种 类 型有助于 识别 无 理数. B B 【 点评 】 实 数运算要 严 格按照法 则进 行 , 特 别 是混合运算 , 注意符号和 顺 序是非常重要的. (1) ( 2015 · 山西百校联考 ) 每年的 10 月 16 日为世界粮食日 , 联合国粮农组织报告显示 , 全球每年约有 13 亿吨食物被浪费 , 每年食物浪费造成的直接经济损失达 7500 亿美元 , 数据 7500 亿美元用科学记数法可表示为 ( ) A . 75×10 10 美元 B . 7.5×10 10 美元 C . 0.75×10 11 美元 D . 7.5×10 11 美元 D (2) 下列近似数中精确到千位的是 ( ) A . 90200 B . 3.450 × 10 2 C . 3.4 × 10 4 D . 3.4 × 10 2 【 点评 】 (1) 科学 记 数法一般表示的数 较 大或很小 , 所以解 题时 一定要仔 细 ; ( 2) 科学 记 数法写出 这 个数后可 还 原成原数 进 行 检验. C [ 对应训练 ] 3 . (1) 近似数 2.5 万精确到 ______ 位. (2) ( 2015 · 宁夏 ) 生物学家发现了一种病毒的长度约为 0.000 004 32 毫米.数据 0.000 004 32 用科学记数法表示为 ( ) A . 0.432 × 10 - 5 B . 4.32 × 10 - 6 C . 4.32 × 10 - 7 D . 43.2 × 10 - 7 千 B 【 例 4 】 (1)( 2015 · 六盘水 ) 下列说法正确的是 ( ) A . | - 2| =- 2 B . 0 的倒数是 0 C . 4 的平方根是 2 D .- 3 的相反数是 3 (2) 已知 | a | = 1 , | b | = 2 , | c | = 3 , 且 a > b > c , 那么 a + b - c = . (3) 设 | a | = 4 , | b | = 2 , 且 | a + b | =- ( a + b ) , 试求 a - b 所有值的和. 解: ∵ |a| = 4 , |b| = 2 , ∴ a = ±4 , b = ±2 , 又 |a + b| =- ( a + b ) ≥ 0 , ∴ a + b ≤ 0 , 可知 a =- 4 , b = ±2 , 所以 a - b =- 4 - 2 =- 6 , 或 a - b =- 4 - ( - 2 ) =- 2 , - 6 + ( - 2 ) =- 8 , a - b 所有值的和是- 8 【 点评 】 (1) 互 为 相反数的两个数和 为 0 ; (2) 正数的 绝对值 是它本身 , 负 数的 绝对值 是它的相反数 , 0 的 绝对值 是 0 ; (3) 两个非 负 数的和 为 0 , 则这 两个数分 别 等于 0. A 1 - 2 1 或- 3 C 【 点评 】 数形 结 合借助数 轴 找到数的位置 , 或由数找到在数 轴 上的点的位置及其相反数的位置 , 再根据数 轴 上右 边 的数大于左 边 的数 , 确定各数的大小或根据大减小 为 正 , 小减大 为负 , 以及有理数的加法、乘法法 则 来确定数的运算后的符号. D D A A A 【 点评 】 实 数的大小比 较 要依据数 值 特点灵活运用比 较 大小的几种方法来 进 行 , 本 题 利用平方比 较 法. < A 试题 若一个实数的 (1) 倒数; (2) 绝对值; (3) 平方; (4) 立方; (5) 平方根; (6) 算术平方根; (7) 立方根等于它的本身 , 则这个数分别为 (1)___________ ; (2)___________________ ; (3)_______ ; (4)___________ ; (5)______ ; (6)_________ ; (7)____________ . 错解 (1)1 ; (2) 正数; (3)1 ; (4)1 或- 1 ; (5)1 ; (6)0 ; (7)1 和- 1. 剖析 对 倒数、 绝对值 、平方、平方根等概念理解不全面是最容易 产 生 错误 的. 1 或- 1 正数或 0( 或非负数 ) 1 或 0 - 1 , 0 或 1 0 0 或 1 - 1 , 0 或 1 C A查看更多