人教版八年级数学(下册)第十七章测试卷(及答案)
人教版八年级数学(下册)
第十七章测试卷
1.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6
B.7,12,13
C.2,3,4
D.1,,
2.在△ABC中,∠A=90°,则下列各式不成立的是( )
A.BC2=AB2+AC2
B.AB2=AC2+BC2
C.AB2=BC2-AC2
D.AC2=BC2-AB2
3.下列说法中正确的是( )
A.在Rt△ABC中,a2+b2=c2
B.在Rt△ABC中,a=3,b=4,那么c=5
C.直角三角形两直角边长都是5,那么斜边长为10
D.直角三角形中,斜边最长
4.一辆拖拉机沿着公路l以20 km/h的速度前行,幼儿园R距离公路l大约3 km,拖拉机产生的噪音能够影响周围5 km的区域,则幼儿园学生受拖拉机噪音影响持续的时间约为( )
A.0.4 h
B.0.8 h
C.1.2 h
D.1.5 h
5.如图1所示,分别以Rt△ABC的三边AB,BC,CA为直径向外作半圆,半圆的面积分别为S1,S2,S3,则S1,S2,S3的关系是( )
图1
A.S1=S2+S3
B.S1
S2+S3
D.无法确定
6.在△ABC中,AB=15,AC=13,高AD=12,则三角形ABC的周长是( )
A.42
B.32
C.42或32
D.37或33
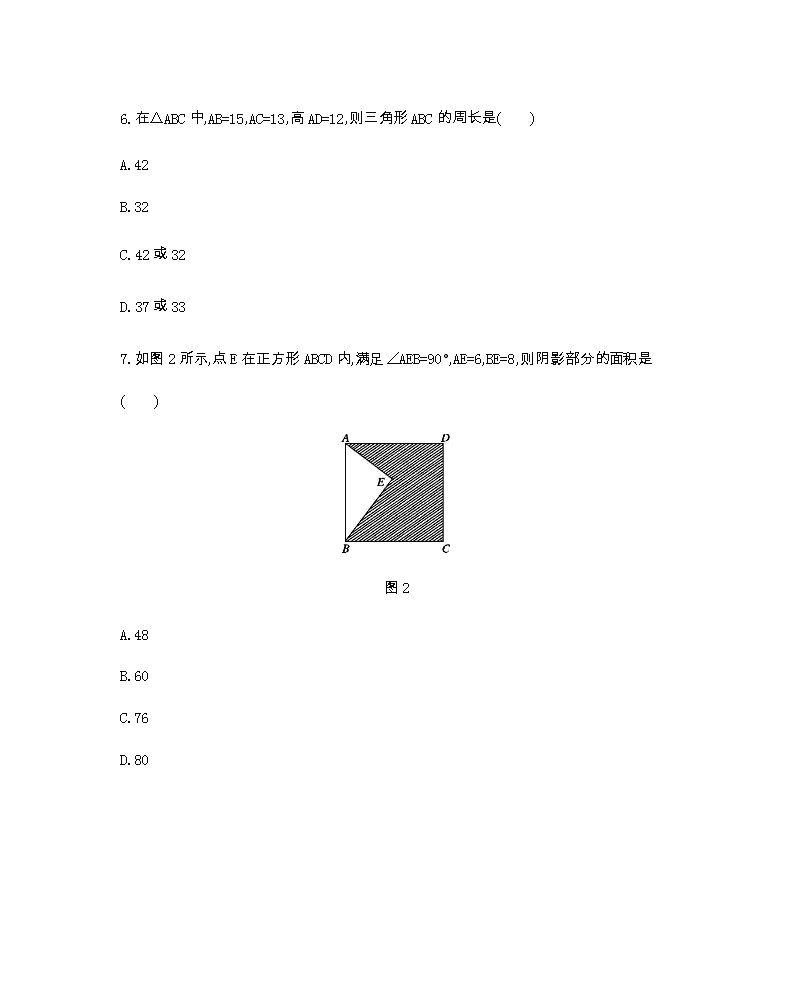
7.如图2所示,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
图2
A.48
B.60
C.76
D.80
8.如图3所示,是一扇高为2 m,宽为1.5 m的门框,现有3块薄木板,尺寸如下:①号木板长3 m,宽2.7 m;②号木板长4 m,宽2.4 m; ③号木板长2.8 m,宽2.8 m.可以从这扇门通过的木板是( )
图3
A.①号
B.②号
C.③号
D.均不能通过
9.写出一组三个整数,使其成为直角三角形的三边,可以是 .
10.如图4所示,在等腰△ABC中,AB=AC,AD是底边上的高,若AB=5 cm,BC=6 cm,则AD= cm.
图4
11.直角三角形的直角边长为8,15,则斜边长为 ,斜边上的高为 .
12.木工做一个长方形桌面,量得桌面的长为60 cm,宽为32 cm,对角线为68 cm,这个桌面 (填“合格”或“不合格”).
13.一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是 .
14.如图5所示,阴影部分(阴影部分为正方形)的面积是 .
图5
15.如图6所示,AD⊥CD,AB=13,BC=12,CD=3,AD=4,则∠CAB+∠B= 度.
图6
16.已知a,b,c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为 .
17.小芳想在墙壁上钉一个三角形的架子(如图7),其中两直角边长度之比为3∶2,斜边长2厘米,求两直角边的长度.
图7
18.在A岛上有一个观测站,上午8时观测站发现在A岛正北方7海里处有一艘船向正东方向航行,上午10时,该船到达距A岛25海里的B岛,求该船的航行速度.
19.某宾馆打算在宽为2米的一段楼梯面上铺上地毯,台阶的侧面如图8所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要多少钱?
图8
20.如图9所示,有一个圆柱,它的高为13 cm,底面周长为10 cm,在圆柱的下底面上A点处有一只蚂蚁想吃到离上底面1 cm处的B点的食物,需爬行的最短距离是多少?
图9
21.如图10所示,某学校(A点)与公路(直线l)的距离为300 m,又与公交车站(D点)的距离为500 m,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
图10
参考答案
1.D
2.B
3.D
4.A
5.A
6.C
7.C
8.B
9.9,40,41(答案不唯一,答对即可)
10.4
11.17,
12.合格
13.120
14.25cm2
15.90
16.等腰直角三角形
17. 解:∵两直角边长度之比为3∶2,
∴设两直角边长分别为:3x厘米、2x厘米.
∵斜边长为2厘米,
∴由勾股定理得:(3x)2+(2x)2=(2)2.
解得:x=2,
3x=3×2=6,
2x=2×2=4.
故两直角边的长度为6厘米,4厘米.
18. 解:如图,由题意得,AC=7海里,AB=25海里,
在Rt△ABC中,BC==24(海里).
∵航行了2小时,
∴船航行的速度为24÷2=12(海里/时).
答:此船的航行速度为12海里/时.
19. 解:如图所示:
利用平移线段,把楼梯的横竖向上向右平移,构成一个长方形,长、宽分别为=12(米)、5米,
所以地毯的长度至少为12+5=17(米),地毯的面积至少为17×2=34(平方米),
所以购买这种地毯至少需要80×34=2 720(元).
答:购买这种地毯至少需要2 720元.
20. 解:如图所示:
根据题意,得BE=EF-FB=13-1=12 (cm).
因为☉O周长为10 cm,所以☉O半周长为5 cm,
即AE=5 cm,BE=12 cm,
所以AB==13 (cm).
答:需爬行的最短距离是13 cm.
21. 解:如图所示:
作AB⊥l于点B,则AB=300 m,AD=500 m.
所以BD=400 m.
设CD=x m,则CB=(400-x)m,
由题意,知AC=CD=x,在Rt△ABC中,
x2=(400-x)2+3002,
x2=160 000+x2-800x+3002,
800x=250 000,
x=312.5.
答:商店与车站之间的距离为312.5 m.