高州市2014届高考数学模拟试题目理

高州市2014届高考数学模拟试题目理

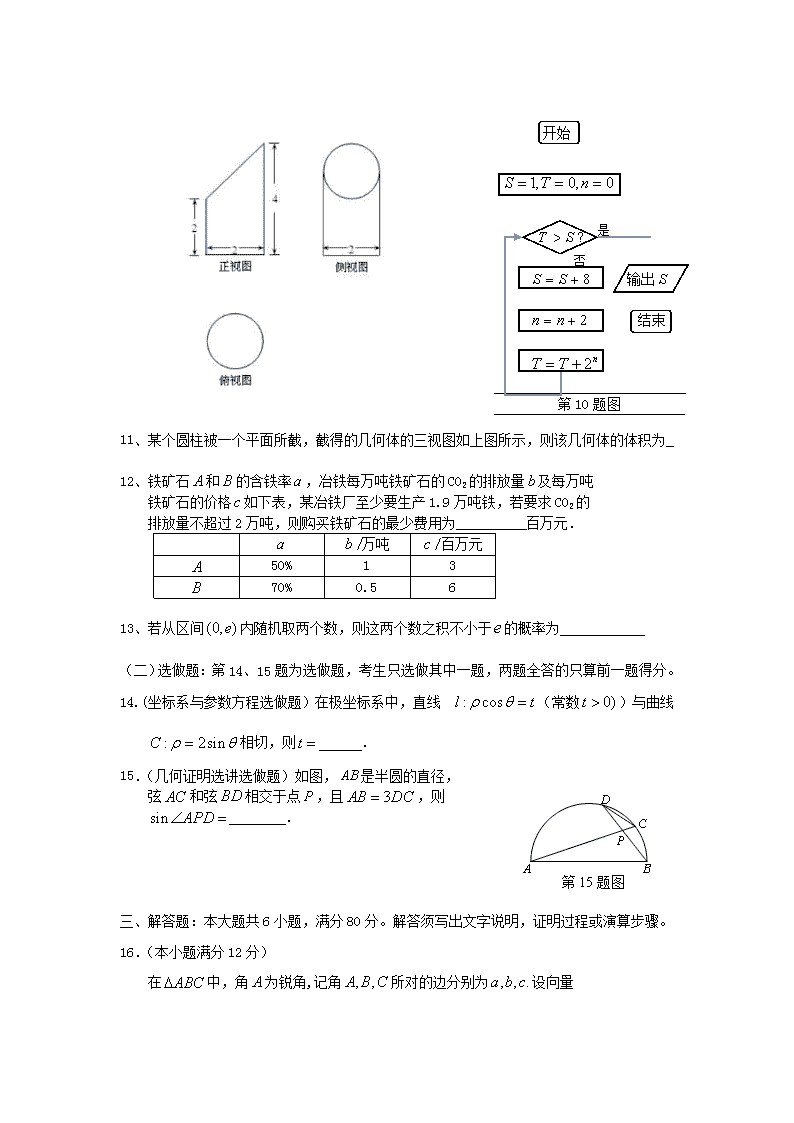
‎2014届高州市高考模拟试题理科数学 本试卷分选择题和非选择题两部分，共4页，满分150分，考试时间120分钟。‎ 注意事项：‎ ‎1、答卷前，考生要务必填写答题卷上的有关项目。‎ ‎2、选择题每小题选出答案后，用2B铅笔把答案填在答题卡相应的位置上。‎ ‎3、非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效。‎ ‎4、考生必须保持答题卷的整洁.考试结束后，将答题卷交回。‎ 第一部分 选择题（共40分）‎ 一、选择题：（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1. 复数的共轭复数是 A. B． C． D．‎ ‎2、已知集合则 A． B． C． D． ‎ ‎3. 下列命题正确的是 A．若直线与平面不平行，则直线与平面内的所有直线都不平行 B．如果两条直线在平面内的射影平行，那么这两条直线平行 C．垂直于同一直线的两个不同平面平行，垂直于同一平面的两条不同直线也平行 D．直线与平面不垂直，则直线与平面内的所有直线都不垂直 ‎4、已知等差数列的公差为2，若成等比数列，则的值为 ‎ A．-4 B．‎-10 C．-8 D．-6‎ ‎5．某班主任对全班50名学生进行了作业量多少的调查，数据如下表：‎ 认为作业多 认为作业不多 总数 喜欢玩电脑游戏 ‎18‎ ‎9‎ ‎27‎ 不喜欢玩电脑游戏 ‎8‎ ‎15‎ ‎23‎ 总数 ‎26‎ ‎24‎ ‎50‎ 根据表中数据得到，参考下表：‎ P(K2≥k)‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ k ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ 则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（ ）‎ ‎ A．97.5% B．95% C．90% D．99.9%‎ ‎6、若，且，则的值等于 A． B． C． D．‎ ‎7．设双曲线C：（）的左、右焦点分别为 F1，F2．若在双曲线的右支上存在一点P，使得 |PF1|＝3|PF2|，则双曲线C的离心率e的取值范围为 ‎ (A) (1,2] (B) (C) (D) (1,2)‎ ‎8、定义在上的函数,如果存在函数为常数,使得对一切实数都成立,则称为函数的一个“承托函数”.现有如下命题：①对给定的函数,其承托函数可能不存在,也可能有无数个；②为函数的一个承托函数；③定义域和值域都是的函数不存在承托函数.其中正确的命题是( ).‎ A.① B.② C.①③ D.②③‎ 第二部分 非选择题（共100分）‎ 二、填空题（本大题共7小题，分为必做题和选做题两部分，每小题5分，满分30分）。‎ ‎（一）必做题：第9至13题为必做题，每道试题考生都必须作答。‎ ‎９、如果展开式中，第四项与第六项的系数相等，则= ，展开式中的常数项的值等于 . ‎ ‎１０、执行下面的程序框图，输出的的值为 ．‎ ‎ 开始 是 否 ‎ ‎ ‎ 输出 ‎ 结束 ‎ ‎ 第10题图 ‎11、某个圆柱被一个平面所截，截得的几何体的三视图如上图所示，则该几何体的体积为 ‎ ‎12、铁矿石和的含铁率，冶铁每万吨铁矿石的CO2的排放量及每万吨 ‎ 铁矿石的价格如下表，某冶铁厂至少要生产1.9万吨铁，若要求CO2的 ‎ 排放量不超过2万吨，则购买铁矿石的最少费用为 百万元．‎ ‎/万吨 ‎/百万元 ‎50%‎ ‎1‎ ‎3‎ ‎70%‎ ‎0.5‎ ‎6‎ ‎13、若从区间内随机取两个数，则这两个数之积不小于的概率为　　　　　　‎ ‎（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的只算前一题得分。‎ ‎14. (坐标系与参数方程选做题）在极坐标系中，直线（常数）与曲线相切，则 ．‎ ‎15．（几何证明选讲选做题）如图，是半圆的直径，‎ 第15题图 弦和弦相交于点，且，则 ‎ ．‎ 三、解答题：本大题共6小题，满分80分。解答须写出文字说明，证明过程或演算步骤。‎ ‎16．（本小题满分12分）‎ 在中，角为锐角,记角所对的边分别为设向量 且与的夹角为 ‎（1）求的值及角的大小；‎ ‎（2）若，求的面积．‎ ‎17、（本小题满分12分）‎ 为庆祝五一，某旅游景点推出“挑战自我”节目，挑战者闯关需要回答三个问题，其中前两个问题回答正确各得10分，回答不正确得0分，第三个题目，回答正确得20分，回答不正确得一10分，总得分不少于30分即可过关。如果一位挑战者回答前两题正确的概率都是,回答第三题正确的概率为，且各题回答正确与否相互之间没有影响。记这位挑战者回答这三个问题的总得分为。‎ ‎ （1)这位挑战者过关的概率有多大？‎ ‎（2）求的概率分布和数学期望。‎ ‎18、（本小题满分14分）‎ ‎ 如图，AB为圆O的直径，点E、F在圆O上，AB//EF，‎ ‎ 矩形ABCD和圆O所在的平面互相垂直.已知AB=2，‎ ‎ EF=1．‎ ‎ (I)求证：平面DAF⊥平面CBF;‎ ‎ (Ⅱ)求直线AB与平面CBF所成角的大小；‎ ‎ (Ⅲ)当AD的长为何值时，二面角D-FE-B的大小为 ‎ 60°?‎ ‎19、（本小题满分14分）‎ 已知数列的前n项和为（），且 ‎（1）求证：是等差数列；‎ ‎（2）求；‎ ‎（3）若，求证：‎ ‎20．（本题满分14分）‎ 已知椭圆的离心率为，以原点为圆心，椭圆短半轴长为半径的圆与直线相切，分别是椭圆的左右两个顶点， 为椭圆上的动点.‎ ‎（Ⅰ）求椭圆的标准方程；‎ ‎（Ⅱ）若与均不重合，设直线与的斜率分别为，证明：为定值；‎ ‎（Ⅲ）为过且垂直于轴的直线上的点，若，求点的轨迹方程，并说明轨迹是什么曲线． ‎ ‎ ‎ ‎21. （本小题满分14分）‎ 设函数，其中b为常数． （1）当时，判断函数f（x）在定义域上的单调性； （2）若函数f（x）的有极值点，求b的取值范围及f（x）的极值点； （3）求证对任意不小于3的正整数n，不等式都成立．‎ 数学试题（理科）参考答案和评分标准 一、选择题：（每题5分，共40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 选项 C ‎ D C D A D A A 二、填空题（每题5分，共30分）‎ ‎9．8，70 10．17 11． 12．15 13． 14．1 15． ‎ ‎15、连结AD，与相似。‎ 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤．‎ ‎16．（本题满分12分）‎ 解：（1）‎ ‎ 3分 ‎，‎ ‎ 5分 ‎ 7分 ‎（2）(法一) ,及,‎ ‎, 即(舍去)或 10分 故 12分 ‎(法二) ,及,‎ ‎. 7分 ‎, ‎ ‎,‎ ‎. 10分 ‎ 故 12分 ‎17．（本题满分12分）‎ 解：（1)这位挑战者有两种情况能过关：‎ ① 第三个答对，前两个一对一错，得20+10+0=30分，‎ ‎ ②三个题目均答对，得10+10+20=40分，．．．．．．．．．.........1分 ‎ 其概率分别为．．．．．．．．．.........2分 ‎ 这位挑战者过关的概率为 ‎(2）如果三个题目均答错，得0+0+（-10）=-10分，‎ ‎ 如果前两个中一对一错，第二个错，得10+0+（-10）=0分；‎ ‎ 前两个错，第三个对，得0+0+20=20分；‎ ‎ 如果前两个对，第三个错，得10+10+（-10) =10分；．．．．．．．．．．．..5分 故的可能取值为：-10， 0，10，20，30，40.．．．．．．……6分 根据的概率分布，可得的期望 ‎18．（本题满分14分）‎ 解：(I)证明：∵平面ABCD⊥平面ABEF，CB⊥AB，‎ ‎ …4分 ‎ (Ⅱ)根据(I)的证明，有AF⊥平面CBF，‎ ‎∴FB为AB在平面CBF上的射影，‎ ‎ ∴∠ABF为直线AB与平面CBF所成的角， ………6分 ‎ ∵AB//EF，∴四边形ABEF为等腰梯形，‎ ‎ 过点F作FH⊥AB，交AB于H．‎ ‎ AB=2, EF=1 ,则 ‎ 在Rt△AFB中，根据射影定理AF2=AH．AB，得AF=1. …………8分 ‎ ‎ ‎ ∴直线AB与平面CBF所成角的大小为30°． ……………9分 ‎ (Ⅲ)（解法一）过A作AG⊥EF于G，连结DG，则∠AGD是二面角D-FE-B的平面角．‎ ‎ ∴∠AGD=60‎ ‎ …………14分 ‎ （解法二）设EF中点为G，以O为坐标原点，OA、OG、AD方向分别为x轴、y轴、z轴 ‎ 方向建立空间直角坐标系（图略）设AD=t(t>O)，则点D的坐标为(1,0,t)‎ ‎ 设平面DEF的法向量为,则 ‎ 即 令解得x=0，y=2t ‎ ………………11分 ‎19．（本题满分14分）‎ 解：（1）∵，‎ ‎………………………………………………….. 2分 ‎………………………………………………….. 3分 ‎ ∴‎ ‎∴数列是等差数列，且………………………………… 5分 ‎（2）当时，……………… 7分 当n=1时，不符合上式……………… 8分 ‎ ∴……………… 9分 ‎（3），……………… 10分 ‎∴.……………… 12分 ‎∴左边显然成立. ……………… 14分 ‎20．（本题满分14分）‎ 解：（Ⅰ）由题意可得圆的方程为，‎ ‎∵直线与圆相切，∴，即， …………………….1分 ‎ 又，即，，解得，， ‎ 所以椭圆方程为．…………………………………………………..3分 ‎ ‎（Ⅱ）设， ，，则，即， ‎ 则，， ……………………………………………….4分 ‎ 即， ‎ ‎∴为定值． …………………………………………………………..6分 ‎ ‎（Ⅲ）设，其中．‎ 由已知及点在椭圆上可得， ‎ 整理得，其中．……………………….8分 ‎ ‎①当时，化简得，‎ 所以点的轨迹方程为，轨迹是两条平行于轴的线段；‎ ‎ …………………………9分 ① 当时，方程变形为，其中，…11分 当时，点的轨迹为中心在原点、实轴在轴上的双曲线满足的部分；‎ 当时，点的轨迹为中心在原点、长轴在轴上的椭圆满足的部分；‎ 当时，点的轨迹为中心在原点、长轴在轴上的椭圆． …………14分 ‎21．（本题满分14分）‎ 解：（1）由题意知，f（x）的定义域为（0，+∞）， ∴当时，f'（x）＞0，函数f（x）在定义域（0，+∞）上单调递增． ‎ ‎…………………3分 （2）①由（Ⅰ）得，当时，函数f（x）在定义域上无极值点． ②时，有两个相同的解， 时， ‎ ‎∴时，函数f（x）在（﹣1，+∞）上无极值点．…………………4分 ③当时，f'（x）=0有两个不同解， ∴（i）b≤0时，，， 此时f'（x），f（x）随x在定义域上的变化情况如表： …………………6分 （ii）当时，0＜x1＜x2＜1 此时，f'（x），f（x）随x的变化情况如下表： …………………8分 综上所述：当且仅当时f（x）有极值点； 当b≤0时，f（x）有惟一最小值点； 当时，f（x）有一个极大值点和一个极小值点 …………………9分 （3）由（2）可知当b=﹣1时，函数f（x）=（x﹣1）2﹣lnx， 此时f（x）有惟一极小值点 且 ‎ ‎…………………11分 令函数h（x）=（x﹣1）﹣lnx（x＞0） ‎ ‎ …………………14分 ‎