八年级下册数学教案 1-4 第1课时 角平分线 北师大版

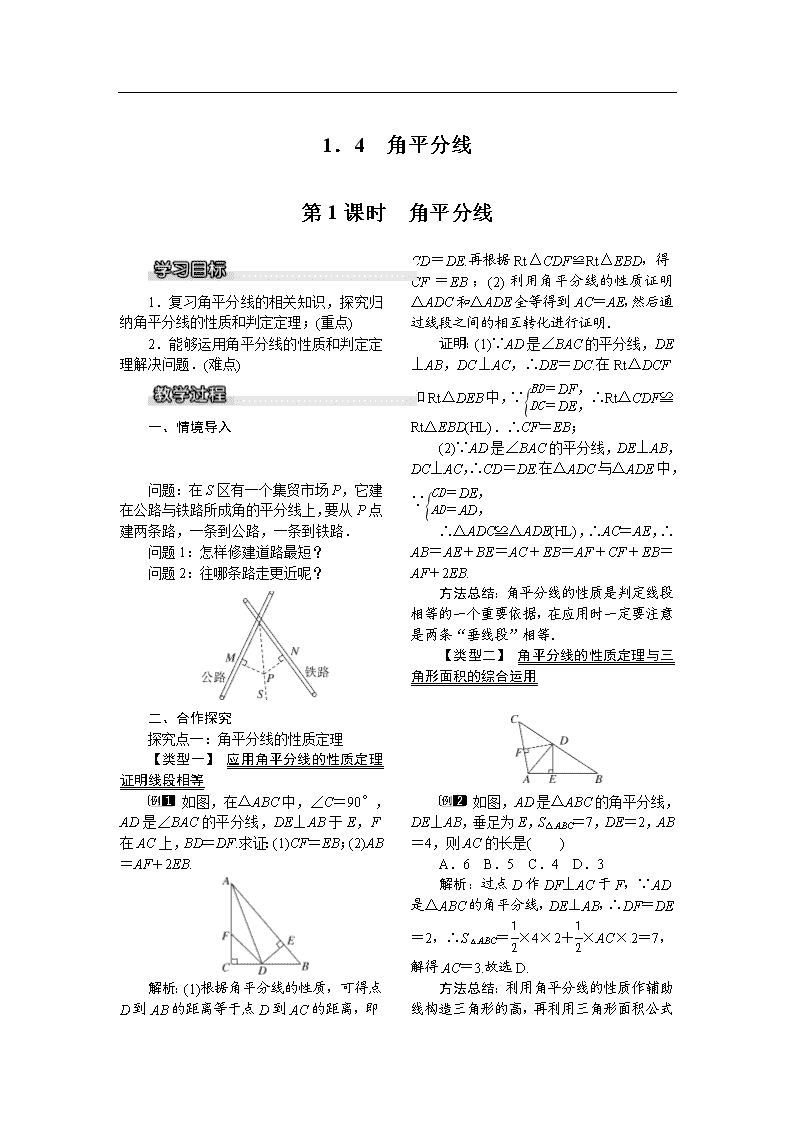
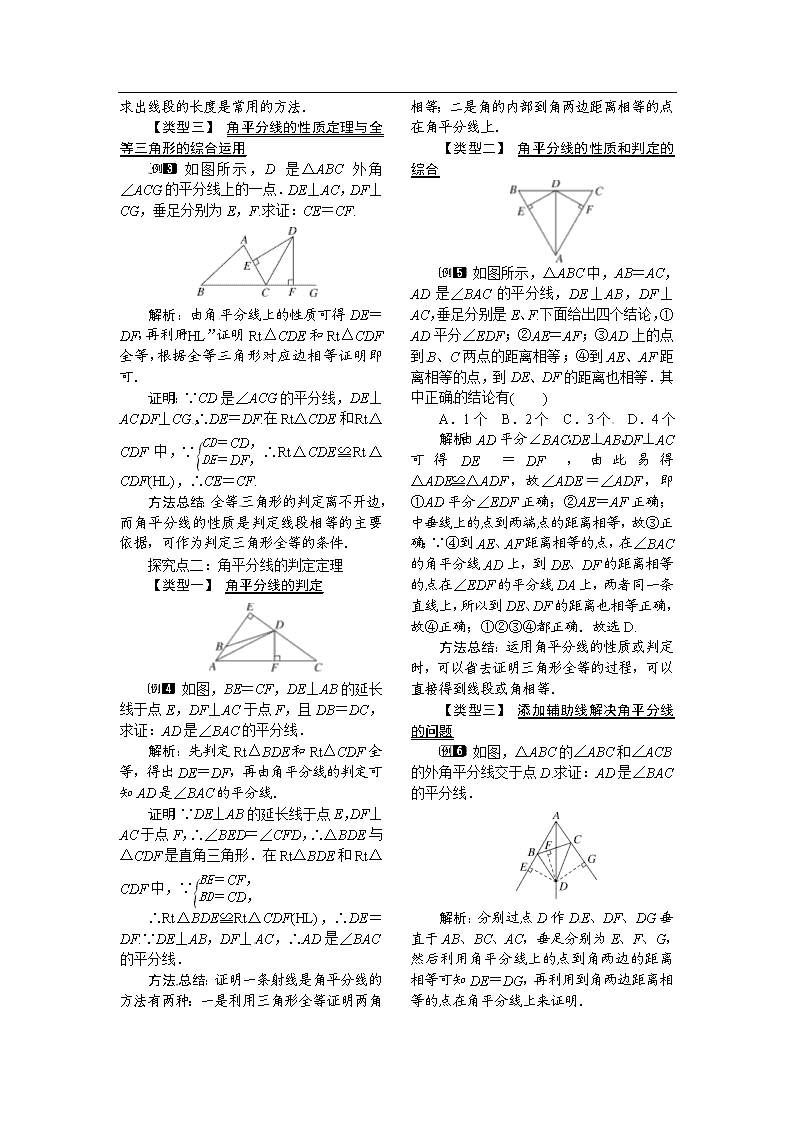
八年级下册数学教案 1-4 第1课时 角平分线 北师大版

‎1．4　角平分线 第1课时　角平分线 ‎1．复习角平分线的相关知识，探究归纳角平分线的性质和判定定理；(重点)‎ ‎2．能够运用角平分线的性质和判定定理解决问题．(难点)‎ 一、情境导入 ‎　　　　　　　　　　　　　　　[来源:学.科.网]‎ ‎[来源:Z_xx_k.Com]‎ 问题：在S区有一个集贸市场P，它建在公路与铁路所成角的平分线上，要从P点建两条路，一条到公路，一条到铁路．‎ 问题1：怎样修建道路最短？‎ 问题2：往哪条路走更近呢？‎ 二、合作探究 探究点一：角平分线的性质定理 ‎【类型一】 应用角平分线的性质定理证明线段相等 ‎ 如图，在△ABC中，∠C＝90°，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，BD＝DF.求证：(1)CF＝EB；(2)AB＝AF＋2EB.‎ 解析：(1)根据角平分线的性质，可得点D到AB的距离等于点D到AC的距离，即CD＝DE.再根据Rt△CDF≌Rt△EBD，得CF＝EB；(2)利用角平分线的性质证明△ADC和△ADE全等得到AC＝AE，然后通过线段之间的相互转化进行证明．[来源:Z,xx,k.Com]‎ 证明：(1)∵AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴DE＝DC.在Rt△DCF和Rt△DEB中，∵∴Rt△CDF≌Rt△EBD(HL)．∴CF＝EB；‎ ‎(2)∵AD是∠BAC的平分线，DE⊥AB，DC⊥AC，∴CD＝DE.在△ADC与△ADE中，∵ ‎∴△ADC≌△ADE(HL)，∴AC＝AE，∴AB＝AE＋BE＝AC＋EB＝AF＋CF＋EB＝AF＋2EB.‎ 方法总结：角平分线的性质是判定线段相等的一个重要依据，在应用时一定要注意是两条“垂线段”相等．‎ ‎【类型二】 角平分线的性质定理与三角形面积的综合运用 ‎[来源:Zxxk.Com]‎ ‎ 如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，S△ABC＝7，DE＝2，AB＝4，则AC的长是(　　)‎ A．6 B．5 C．4 D．3‎ 解析：过点D作DF⊥AC于F，∵AD是△ABC的角平分线，DE⊥AB，∴DF＝DE＝2，∴S△ABC＝×4×2＋×AC×2＝7，解得AC＝3.故选D.‎ 方法总结：利用角平分线的性质作辅助线构造三角形的高，‎ 再利用三角形面积公式求出线段的长度是常用的方法．‎ ‎【类型三】 角平分线的性质定理与全等三角形的综合运用 ‎ 如图所示，D是△ABC外角∠ACG的平分线上的一点．DE⊥AC，DF⊥CG，垂足分别为E，F.求证：CE＝CF.‎ ‎[来源:学科网]‎ 解析：由角平分线上的性质可得DE＝DF，再利用“HL”证明Rt△CDE和Rt△CDF全等，根据全等三角形对应边相等证明即可．‎ 证明：∵CD是∠ACG的平分线，DE⊥AC，DF⊥CG，∴DE＝DF.在Rt△CDE和Rt△CDF中，∵∴Rt△CDE≌Rt△CDF(HL)，∴CE＝CF.‎ 方法总结：全等三角形的判定离不开边，而角平分线的性质是判定线段相等的主要依据，可作为判定三角形全等的条件．‎ 探究点二：角平分线的判定定理 ‎【类型一】 角平分线的判定 ‎ 如图，BE＝CF，DE⊥AB的延长线于点E，DF⊥AC于点F，且DB＝DC，求证：AD是∠BAC的平分线．‎ 解析：先判定Rt△BDE和Rt△CDF全等，得出DE＝DF，再由角平分线的判定可知AD是∠BAC的平分线．‎ 证明：∵DE⊥AB的延长线于点E，DF⊥AC于点F，∴∠BED＝∠CFD，∴△BDE与△CDF是直角三角形．在Rt△BDE和Rt△CDF中，∵ ‎∴Rt△BDE≌Rt△CDF(HL)，∴DE＝DF.∵DE⊥AB，DF⊥AC，∴AD是∠BAC的平分线．‎ 方法总结：证明一条射线是角平分线的方法有两种：一是利用三角形全等证明两角相等；二是角的内部到角两边距离相等的点在角平分线上．‎ ‎【类型二】 角平分线的性质和判定的综合 ‎ 如图所示，△ABC中，AB＝AC，AD是∠BAC的平分线，DE⊥AB，DF⊥AC，垂足分别是E、F.下面给出四个结论，①AD平分∠EDF；②AE＝AF；③AD上的点到B、C两点的距离相等；④到AE、AF距离相等的点，到DE、DF的距离也相等．其中正确的结论有(　　)‎ A．1个 B．2个 C．3个 D．4个 解析：由AD平分∠BAC，DE⊥AB，DF⊥AC可得DE＝DF，由此易得△ADE≌△ADF，故∠ADE＝∠ADF，即①AD平分∠EDF正确；②AE＝AF正确；中垂线上的点到两端点的距离相等，故③正确；∵④到AE、AF距离相等的点，在∠BAC的角平分线AD上，到DE、DF的距离相等的点在∠EDF的平分线DA上，两者同一条直线上，所以到DE、DF的距离也相等正确，故④正确；①②③④都正确．故选D.‎ 方法总结：运用角平分线的性质或判定时，可以省去证明三角形全等的过程，可以直接得到线段或角相等．‎ ‎【类型三】 添加辅助线解决角平分线的问题 ‎ 如图，△ABC的∠ABC和∠ACB的外角平分线交于点D.求证：AD是∠BAC的平分线．‎ 解析：分别过点D作DE、DF、DG垂直于AB、BC、AC，垂足分别为E、F、G，然后利用角平分线上的点到角两边的距离相等可知DE＝DG，再利用到角两边距离相等的点在角平分线上来证明．‎ 证明：分别过D作DE、DF、DG 垂直于AB、BC、AC，垂足分别为E、F、G.∵BD平分∠CBE，DE⊥BE，DF⊥BC，∴DE＝DF.同理DG＝DF，∴DE＝DG，∴点D在∠BAC的平分线上，∴AD是∠BAC的平分线．‎ 方法总结：在遇到角平分线的问题时，往往过角平分线上的一点作角两边的垂线段，利用角平分线的判定或性质解决问题．‎ ‎【类型四】 线段垂直平分线与角平分线的综合运用 ‎ 如图，在四边形ADBC中，AB与CD互相垂直平分，垂足为点O.‎ ‎(1)找出图中相等的线段；‎ ‎(2)OE，OF分别是点O到∠CAD两边的垂线段，试说明它们的大小有什么关系．‎ 解析：(1)由垂直平分线的性质可得出相等的线段；(2)由条件可证明△AOC≌△AOD，可得AO平分∠DAC，根据角平分线的性质可得OE＝OF.‎ 解：(1)∵AB、CD互相垂直平分，∴OC＝OD，AO＝OB，且AC＝BC＝AD＝BD；‎ ‎(2)OE＝OF，理由如下：在△AOC和△AOD中，∵∴△AOC≌△AOD(SSS)，∴∠CAO＝∠DAO.又∵OE⊥AC，OF⊥AD，∴OE＝OF.‎ 方法总结：本题是线段垂直平分线的性质和角平分线的性质的综合，掌握它们的适用条件和表示方法是解题的关键．‎ 三、板书设计 ‎1．角平分线的性质定理 角平分线上的点到这个角的两边的距离相等．‎ ‎2．角平分线的判定定理 在一个角的内部，到角的两边距离相等的点在这个角的平分线上．‎ 本节课由于采用了动手操作以及讨论交流等教学方法，从而有效地增强了学生对角以及角平分线的性质的感性认识，提高了学生对新知识的理解与感悟，因而本节课的教学效果较好，学生对所学的新知识掌握较好，达到了教学的目的．不足之处是少数学生在性质的运用上还存在问题，需要在今后的教学与作业中进一步的加强巩固和训练.‎