- 2021-04-12 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
角平分线(1)教案
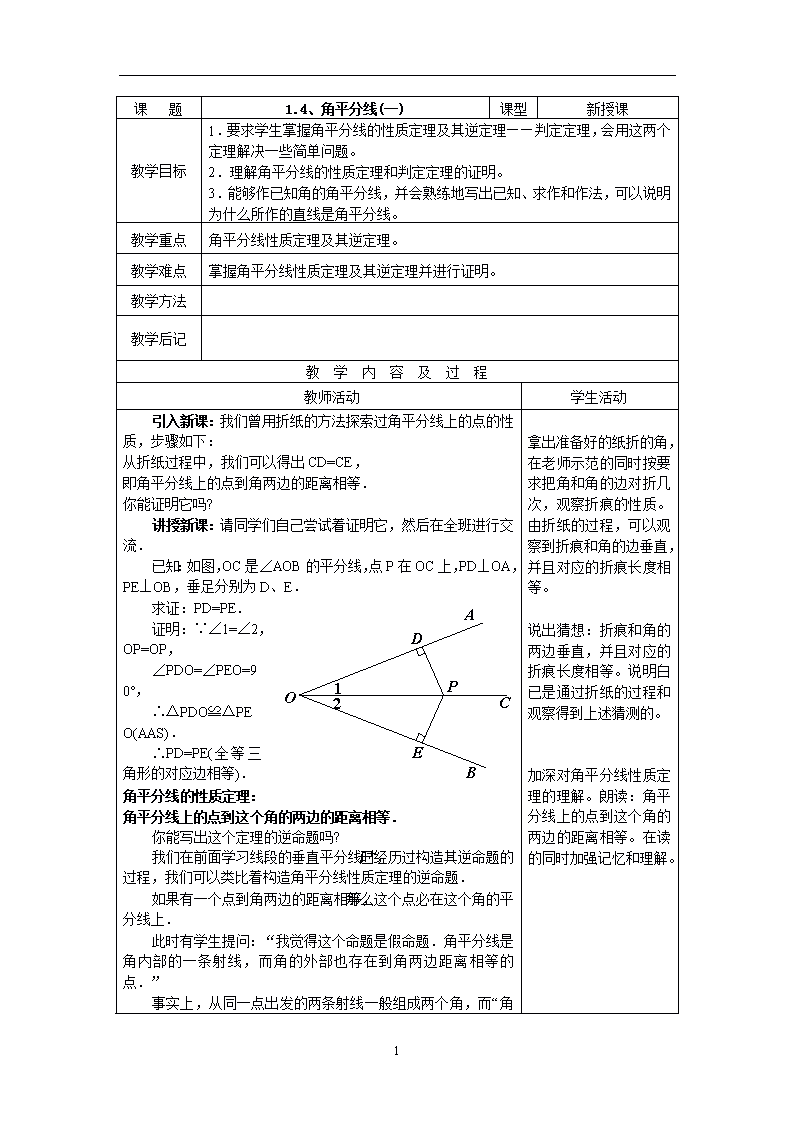
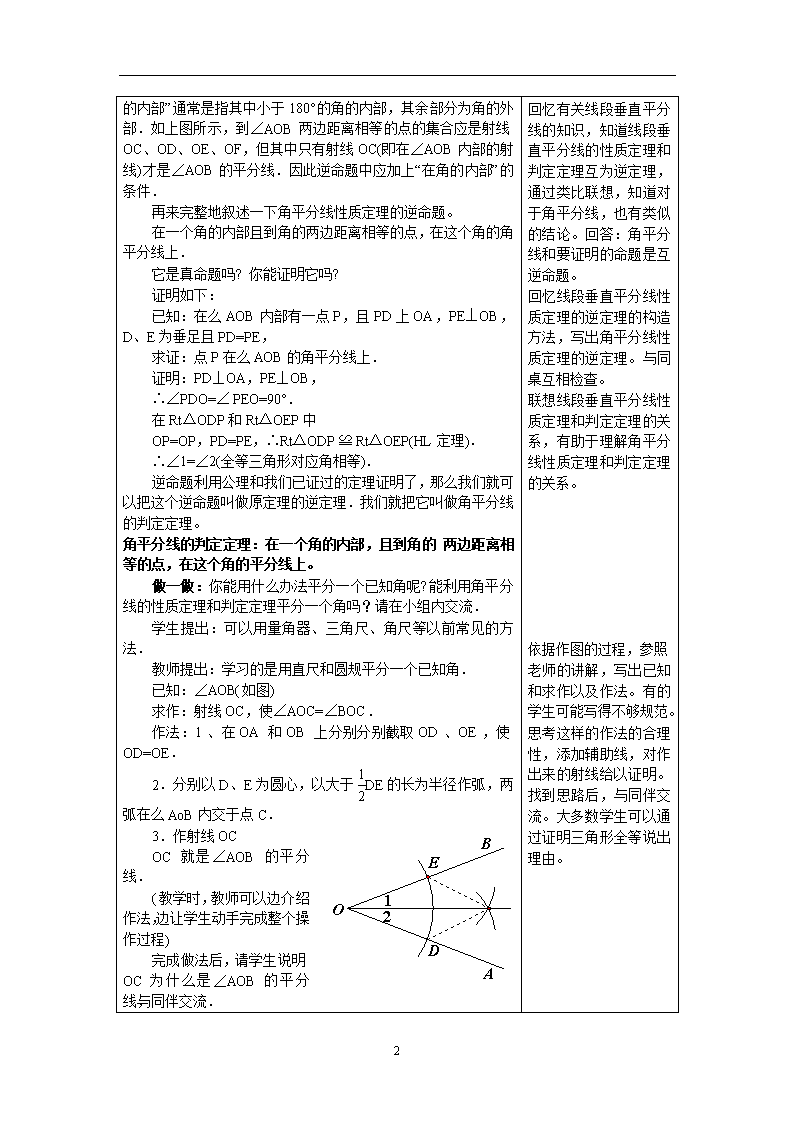
课 题 1.4、角平分线(一) 课型 新授课 教学目标 1.要求学生掌握角平分线的性质定理及其逆定理——判定定理,会用这两个定理解决一些简单问题。 2.理解角平分线的性质定理和判定定理的证明。 3.能够作已知角的角平分线,并会熟练地写出已知、求作和作法,可以说明为什么所作的直线是角平分线。 教学重点 角平分线性质定理及其逆定理。 教学难点 掌握角平分线性质定理及其逆定理并进行证明。 教学方法 教学后记 教 学 内 容 及 过 程 教师活动 学生活动 引入新课:我们曾用折纸的方法探索过角平分线上的点的性质,步骤如下: 从折纸过程中,我们可以得出CD=CE, 即角平分线上的点到角两边的距离相等. 你能证明它吗? 讲授新课:请同学们自己尝试着证明它,然后在全班进行交流. 已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E. 求证:PD=PE. 证明:∵∠1=∠2,OP=OP, ∠PDO=∠PEO=90°, ∴△PDO≌△PEO(AAS). ∴PD=PE(全等三角形的对应边相等). 角平分线的性质定理:角平分线上的点到这个角的两边的距离相等. 你能写出这个定理的逆命题吗? 我们在前面学习线段的垂直平分线时,已经历过构造其逆命题的过程,我们可以类比着构造角平分线性质定理的逆命题. 如果有一个点到角两边的距离相等,那么这个点必在这个角的平分线上. 此时有学生提问:“我觉得这个命题是假命题.角平分线是角内部的一条射线,而角的外部也存在到角两边距离相等的点.” 事实上,从同一点出发的两条射线一般组成两个角,而“ 拿出准备好的纸折的角,在老师示范的同时按要求把角和角的边对折几次,观察折痕的性质。由折纸的过程,可以观察到折痕和角的边垂直,并且对应的折痕长度相等。 说出猜想:折痕和角的两边垂直,并且对应的折痕长度相等。说明白已是通过折纸的过程和观察得到上述猜测的。 加深对角平分线性质定理的理解。朗读:角平分线上的点到这个角的两边的距离相等。在读的同时加强记忆和理解。 3 角的内部”通常是指其中小于180°的角的内部,其余部分为角的外部.如上图所示,到∠AOB两边距离相等的点的集合应是射线OC、OD、OE、OF,但其中只有射线OC(即在∠AOB内部的射线)才是∠AOB的平分线.因此逆命题中应加上“在角的内部”的条件. 再来完整地叙述一下角平分线性质定理的逆命题。 在一个角的内部且到角的两边距离相等的点,在这个角的角平分线上. 它是真命题吗? 你能证明它吗? 证明如下: 已知:在么AOB内部有一点P,且PD上OA,PE⊥OB,D、E为垂足且PD=PE, 求证:点P在么AOB的角平分线上. 证明:PD⊥OA,PE⊥OB, ∴∠PDO=∠ PEO=90°. 在Rt△ODP和Rt△OEP中 OP=OP,PD=PE,∴Rt△ODP ≌ Rt△OEP(HL定理). ∴∠1=∠2(全等三角形对应角相等). 逆命题利用公理和我们已证过的定理证明了,那么我们就可以把这个逆命题叫做原定理的逆定理.我们就把它叫做角平分线的判定定理。 角平分线的判定定理:在一个角的内部,且到角的 两边距离相等的点,在这个角的平分线上。 做一做:你能用什么办法平分一个已知角呢?能利用角平分线的性质定理和判定定理平分一个角吗?请在小组内交流. 学生提出:可以用量角器、三角尺、角尺等以前常见的方法. 教师提出:学习的是用直尺和圆规平分一个已知角. 已知:∠AOB(如图) 求作:射线OC,使∠AOC=∠BOC. 作法:1、在OA和OB上分别分别截取OD、OE,使OD=OE. 2.分别以D、E为圆心,以大于DE的长为半径作弧,两弧在么AoB内交于点C. 3.作射线OC OC就是∠AOB的平分线. (教学时,教师可以边介绍作法,边让学生动手完成整个操作过程) 完成做法后,请学生说明OC为什么是∠AOB的平分线,与同伴交流. 回忆有关线段垂直平分线的知识,知道线段垂直平分线的性质定理和判定定理互为逆定理,通过类比联想,知道对于角平分线,也有类似的结论。回答:角平分线和要证明的命题是互逆命题。 回忆线段垂直平分线性质定理的逆定理的构造方法,写出角平分线性质定理的逆定理。与同桌互相检查。 联想线段垂直平分线性质定理和判定定理的关系,有助于理解角平分线性质定理和判定定理的关系。 依据作图的过程,参照 老师的讲解,写出已知和求作以及作法。有的学生可能写得不够规范。 思考这样的作法的合理性,添加辅助线,对作出来的射线给以证明。找到思路后,与同伴交流。大多数学生可以通过证明三角形全等说出理由。 3 从作图的过程中,不难发现OD=OE,CE=CD,OC=OC, △OCEC≌△OCD(SSS). ∴∠1=∠2,即OC是∠AOB的角平分线. 随堂练习 如图,AD、AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系? 解:∵AD平分∠CAB. ∴又∠1=∠2=12 ∠CAB 又∵AE平分∠CAF. ∠CAB+∠CAF=180°, ∴∠3=∠4= 12 ∠CAF ∵∠CAB+∠CAF=180° ∴∠1+∠3= 12 (∠CAB+∠CAF)=12 ×180°=90°,即AD⊥AE. 作业:1、2、3题 板书设计: 一、角平分线性质定理 二、角平分线判定定理 三、用直尺和圆规作角的平分线 3查看更多