中考数学几何证明题分类汇编6

中考数学几何证明题分类汇编6

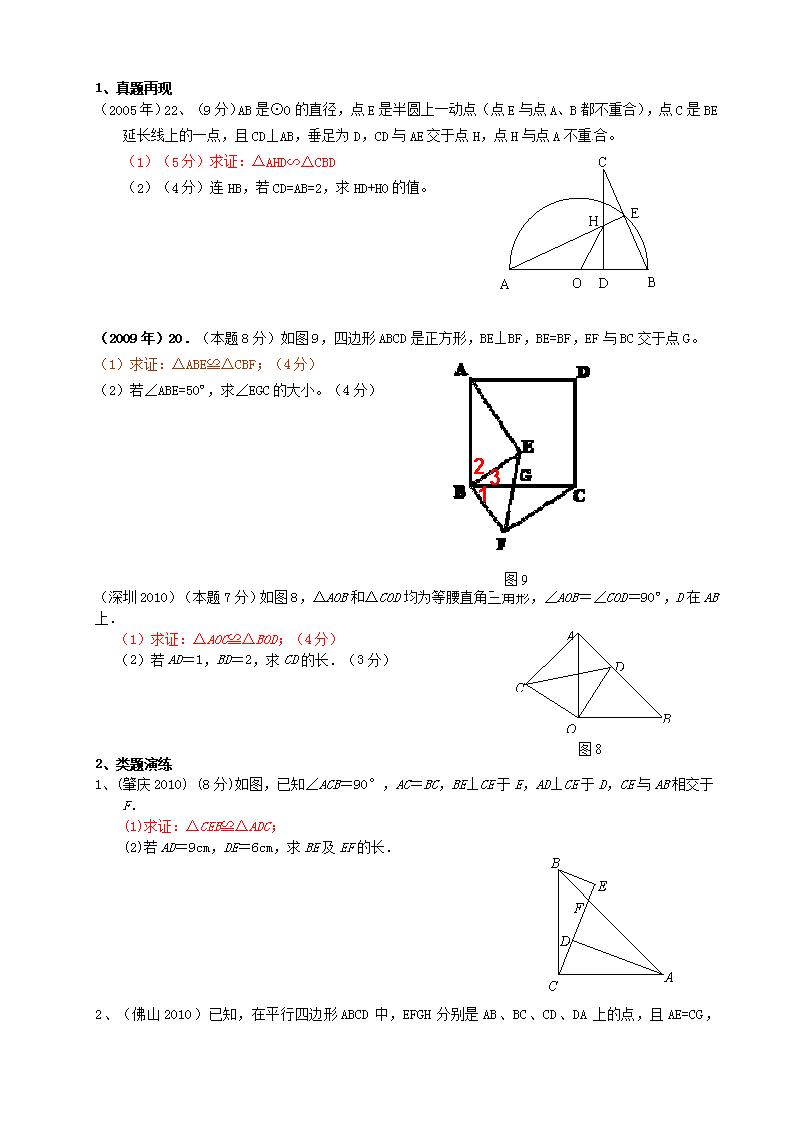
几何证明题分类汇编 ‎ ‎ 一、证明两线段相等 ‎ ‎1、真题再现 图3‎ ‎（2007年深圳）18．如图3，在梯形中，，，是上一点，，．‎ ‎（1）求证：．‎ ‎（2）若，求的长．‎ ‎（2011年）21、（8分）如图11，一张矩形纸片ABCD，其中AD=8cm，AB=6cm，先沿对角线BD折叠，点C落在点C′的位置，BC′交AD于点G.‎ ‎（1）求证：AG=C′G；‎ ‎（2）如图12，再折叠一次，使点D与点A重合，的折痕EN，EN角AD于M，求EM的长.‎ ‎2、类题演练 A B C D E F 第20题图 ‎1、（汕头2010）如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE．已知∠BAC=30º，EF⊥AB，垂足为F，连结DF．‎ ‎（1）试说明AC=EF；‎ ‎（2）求证：四边形ADFE是平行四边形．‎ ‎2．（梅州2010）如图，在△ABC中，点P是边AC上的一个动点，过点P作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．‎ ‎(1)求证：PE＝PF；‎ ‎(2)*当点P在边AC上运动时，四边形BCFE可能是菱形吗？说明理由；‎ A B C D M N E F P ‎(3)*若在AC边上存在点P，使四边形AECF是正方形，且＝．求此时∠A的大小．‎ 二、证明两角相等、三角形相似及全等 ‎1、真题再现 A O D B H E C ‎（2005年）22、（9分）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合。‎ ‎ （1）（5分）求证：△AHD∽△CBD ‎ （2）（4分）连HB，若CD=AB=2，求HD+HO的值。‎ 图9‎ ‎（2009年）20．（本题8分）如图9，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G。‎ ‎（1）求证：△ABE≌△CBF；（4分）‎ ‎（2）若∠ABE=50º，求∠EGC的大小。（4分）‎ ‎ ‎ ‎（深圳2010）（本题7分）如图8，△AOB和△COD均为等腰直角三角形，∠AOB＝∠COD＝90º，D在AB上．‎A B C D 图8‎ O ‎（1）求证：△AOC≌△BOD；（4分）‎ ‎（2）若AD＝1，BD＝2，求CD的长．（3分）‎ ‎2、类题演练 ‎1、(肇庆2010) (8分)如图，已知∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D，CE与AB相交于F．‎ ‎(1)求证：△CEB≌△ADC；‎ A B C D F E ‎(2)若AD＝9cm，DE＝6cm，求BE及EF的长．‎ ‎2、（佛山2010）已知，在平行四边形ABCD中，EFGH分别是AB、BC、CD、DA上的点，且AE=CG，BF=DH，求证：≌‎ G A E B F C D H O B C A E D O B C D A E 图1‎ 图2‎ ‎3、（茂名2010）如图，已知OA⊥OB，OA＝4，OB＝3，以AB为边作矩形ABCD，使AD＝a，过点D作DE垂直OA的延长线交于点E．‎ ‎(1)证明：△OAB∽△EDA；‎ ‎(2)当a为何值时，△OAB≌△EDA？*请说明理由，并求此时点 C到OE的距离．‎ 三、证明两直线平行 ‎1、真题再现 ‎（2006年）22．(10分)如图10-1，在平面直角坐标系中，点在轴的正半轴上， ⊙交轴于 两点，交轴于两点，且为的中点，交轴于点，若点的坐标为（－2，0），‎ ‎(1)(3分)求点的坐标. ‎ ‎(2)(3分)连结，求证：∥‎ ‎2、类题演练 ‎1、(湛江2010) (10分)如图，在□ABCD中，点E、F是对角线BD上的两点，且BE＝DF．‎ A B C D E F 求证：(1)△ABE≌△CDF；(2)AE∥CF．‎ 四、证明两直线互相垂直 ‎1、真题再现 ‎（2006年）18．（７分）如图7，在梯形ABCD中，AD∥BC, ，‎ A D B C 图7‎ ‎．‎ ‎（1）（３分）求证： ‎ ‎（2）（４分）若，求梯形ABCD的面积 ‎2、类题演练 ‎1．已知：如图，在△中，是边上一点，⊙过三点，．‎ ‎（1）求证：直线是⊙的切线；‎ ‎（2）如果，⊙的半径为，求的长．‎ ‎2、如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点D恰好为BC的中点.过点D作⊙O的切线交AC边于点E.‎ ‎（第2题图）‎ ‎（1）求证：DE⊥AC；‎ ‎（2）若∠ABC=30°，求tan∠BCO的值.‎ ‎3．（2011年深圳二模） 如图所示，矩形ABCD中，点E在CB的延长线上，使CE＝AC，连结AE，点F是AE的中点，连结BF、DF，求证：BF⊥DF 第3题图 五、证明比例式或等积式 ‎1、真题再现 ‎1．（2011年深圳二模）已知⊙O的直径AB、CD互相垂直，弦AE交CD于F，若⊙O的半径为R求证：AE·AF＝2 R ‎2、类题演练 第1题图 ‎1．（2011年深圳二模）在△ABC中，AC＝BC，∠ACB＝90°，D、E是直线AB上两点．∠DCE＝45°‎ ‎（１）当CE⊥AB时，点D与点A重合，显然DE＝AD＋BE（不必证明）‎ ‎（２）如图，当点D不与点A重合时，求证：DE＝AD＋BE ‎（３）当点D在BA的延长线上时，（２）中的结论是否成立？画出图形，说明理由． ‎ ‎2.（2011深圳市三模）（本小题满分10分）‎ 如图，已知△ABC，∠ACB=90º，AC=BC，点E、F在AB上，∠ECF=45º，‎ ‎　　（1）求证：△ACF∽△BEC（5分）‎ ‎　　（2）设△ABC的面积为S，求证：AF·BE=2S（3）‎ ‎3.（2011深圳市四模）（2）如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于D.‎ ‎①求证：AB2=AD·AC.‎ ‎②当点D运动到半圆AB什么位置时，△ABC为等腰直角三角形，为什么？‎ A B C D O·‎ 第3（2）题图 ‎4、（本小题满分9分）‎ 如图，为的直径，劣弧，连接并延长交于．‎ 求证：（1）是的切线；‎ 第4题图 O A E D B C ‎（2）．‎ ‎5. 如图所示，⊙O中，弦AC、BD交于E，。‎ ‎ （1）求证：；‎ ‎ （2）延长EB到F，使EF=CF，试判断CF与⊙O的位置关系，并说明理由。‎ 六、证明角的和、差、倍、分 ‎1、真题再现 ‎（2009年深圳）21．（本题8分）如图10，AB是⊙O的直径，AB=10，‎ 图10‎ DC切⊙O于点C，AD⊥DC，垂足为D，AD交⊙O于点E。‎ ‎（1）求证：AC平分∠BAD；（4分）‎ ‎（2）若sin∠BEC=，求DC的长。（4分）‎ ‎2、类题演练 ‎1、（广州2010）如图5，在等腰梯形ABCD中，AD∥BC．‎ 求证：∠A＋∠C＝180°‎ ‎2、如图，在中，点在斜边上，以为直径的与相切于点 ‎（1）求证：平分 ‎（2）若 ‎①求的值；②求图中阴影部分的面积.‎ ‎3、如图，是的直径，点在的延长线上，直线与相切于点，弦于点，线段，连接.‎ ‎（1）求证：；‎ 第3题图 D B O E A C F ‎（2）若求的半径及的长.‎ 七、证明线段的和、差、倍、分 ‎1、真题再现 ‎（2005年）22、（9分）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合。‎ ‎ （1）（5分）求证：△AHD∽△CBD A O D B H E C ‎ （2）（4分）连HB，若CD=AB=2，求HD+HO的值。‎ ‎2、类题演练 ‎1．（1）如图1，已知矩形ABCD中，点E是BC上的一动点，过点E作EF⊥BD于点F，EG⊥AC于点G，CH⊥BD于点H，试证明CH=EF+EG;‎ ‎(2) 若点E在ＢＣ的延长线上，如图2，过点E作EF⊥BD于点F，EG⊥AC的延长线于点G，CH⊥BD于点H， 则EF、EG、ＣH三者之间具有怎样的数量关系，直接写出你的猜想；‎ ‎ (3) 如图3，BD是正方形ABCD的对角线,L在BD上，且BL=BC, 连结CL，点E是CL上任一点, EF⊥BD于点F，EG⊥BC于点G，猜想EF、EG、BD之间具有怎样的数量关系，直接写出你的猜想；‎ ‎ (4) 观察图1、图2、图3的特性，请你根据这一特性构造一个图形， 使它仍然具有EF、EG、ＣH这样的线段，并满足（1）或（2）的结论，写出相关题设的条件和结论.‎ ‎2. 设点E是平行四边形ABCD的边AB的中点，F是BC边上一点，线段DE和AF相交于点P，点Q在线段DE上，且AQ∥PC．‎ ‎(1)证明：PC＝2AQ．‎ ‎(2)当点F为BC的中点时，试比较△PFC和梯形APCQ面积的大小关系，并对你的结论加以证明．‎ 八、其他 ‎1、真题再现 ‎（08年深圳中考）如图5，在梯形ABCD中，AB∥DC， DB平分∠ADC，过点A作AE∥BD，交CD的 延长线于点E，且∠C＝2∠E．‎ ‎（1）求证：梯形ABCD是等腰梯形．‎ ‎（2）若∠BDC＝30°，AD＝5，求CD的长．‎ ‎2、类题演练 ‎1．(肇庆2010)如图，四边形ABCD是平行四边形，AC、BD交于点O，∠1＝∠2．‎ ‎1‎ ‎2‎ A C O B D ‎﹚‎ ‎﹙‎ ‎(1)求证：四边形ABCD是矩形；‎ ‎(2)若∠BOC＝120°，AB＝4cm，求四边形ABCD的面积．‎ 图（2）‎ ‎2..如图（2），是的直径，是圆上一点，＝，连结过点作弦的平行线 ‎（1）求证：是的切线；‎ ‎（2）已知求弦BC的长.‎ ‎3.（本题8分），如图，四边形是平行四边形，以为直径的经过点是上一点，且 ‎ （1）试判断与的位置关系，并说明理由；‎ ‎ （2）若的半径为，求的正弦值.‎ B A D C E O ‎（第3题）‎